Devoir commun de maths en première S, ce sujet du devoir en commun pour les élèves en 1ère S dure 3 h et porte sur de nombreux chapitres.Il est destiné aux élèves de première S et aux enseignants du lycée.
Cet exercice est un questionnaire à choix multiple (QCM). Pour chaque question, une seule des quatre réponses
proposées est correcte.
Une réponse juste rapporte un point ; une réponse fausse ou l’absence de réponse n’apporte pas de point et n’en retire pas.
Relevez sur votre copie le numéro de la question ainsi que la lettre correspondant à la réponse choisie.
Aucune justification n’est demandée.
On note f la fonction définie sur R dont la courbe représentative (C) est la parabole donnée en annexe (dernière page
du sujet). Le point A(4 ; 0) appartient à la courbe (C) et la droite (d) est la tangente à la courbe (C) au point A.
On considère la fonction f définie sur [0; 15] par 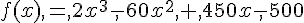 .
.
1. a. Calculer f′(x).
b. Étudier le signe de f′(x) sur [0;15].
c. En déduire le tableau de variations de f sur [0; 15].
d. On admet que l’équation f(x) = 0 a 2 solutions distinctes dans l’intervalle [0;15].
Donner des valeurs approchées, à 10−1 près, de ces solutions notées α et β.
2. Un fabricant envisage la production de boîtes en forme de pavé droit pour emballer des clous en découpant deux
bandes de même largeur dans une feuille de carton carrée.
Le côté de la feuille mesure 30 cm et on désigne par x la mesure en cm de la largeur des bandes découpées. On
admet que  .
.
a. Calculer le volume de la boîte si x = 2.
b. Justifier que le volume V (x), en cm3, de la boîte est V (x) = (15 − x)(30 − 2x)x.
c. Vérifier que le volume V (x) est égal à f(x) + 500, où f est la fonction définie précédemment.
d. En déduire la valeur de x pour laquelle le volume de la boîte est maximal. Préciser la valeur du volume maximal.
3. Le fabricant veut des boîtes de 500 cm3. Combien a-t-il de possibilités? Justifier la réponse.
Une urne contient n boules indiscernables au toucher : 5 boules rouges et n − 5 boules noires (n est un entier supérieur
ou égal à 6).
Un joueur tire au hasard successivement et sans remise deux boules de l’urne.
1. Construire un arbre pondéré décrivant cette expérience aléatoire.
Le joueur gagne 2 euros si les deux boules tirées sont de couleurs différentes et perd 1 euro sinon. On note A
l’événement : «les deux boules tirées sont de couleurs différentes »et X la variable aléatoire donnant le gain algébrique
du joueur.
ABC est un triangle quelconque.
On souhaite démontrer que les droites (AJ), (BK) et (CI) sont concourantes.
Soit E le point d’intersection des droites (AJ) et (BK).
Donner, sans justification, les coordonnées des points B, C, A, I et J.
Calculer les coordonnées du point K.
Déterminer une équation cartésienne de la droite (AJ) et montrer qu’elle peut se mettre sous la forme
3x + y − 1 = 0 .
Déterminer une équation cartésienne de la droite (BK).
En déduire les coordonnées du point E.
Soit la suite U de terme général Un définie pour tout entier naturel n.
Montrer que U1 = 2 et que U2 = 6. Calculer U3.
On considère l’algorithme suivant :
Début de l’algorithme
Entrée: Saisir N un entier naturel non nul
Initialisation: AffecteràP la valeur 0
Traitement: PourK allant de 0 à N :
Affecter à P la valeur P + K
Afficher P
Fin Pour
Fin de l’algorithme
a. Faire fonctionner l’algorithme avec N = 3. Obtient-on à l’affichage les valeurs des quatre premiers termes de
la suite U ?
b. Recopier la partie Traitement de cet algorithme en la modifiant, de manière à obtenir à l’affichage les valeurs
des N + 1 premiers termes de la suite U.
Sujet du devoir en commun de maths en première S
Corrigé du devoir en commun de maths en première S






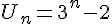 et la suite (U_n) définie par
et la suite (U_n) définie par 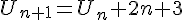 .
.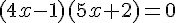 .
.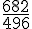 pour la rendre irréductible, en indiquant la méthode.
pour la rendre irréductible, en indiquant la méthode.
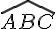 : dans le triangle ABC
: dans le triangle ABC .
. (DG) et M
(DG) et M 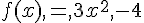 .
.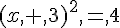 .
.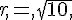 .
.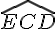 arrondie à 0,1° près.
arrondie à 0,1° près.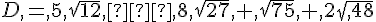 sous la forme
sous la forme 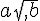 avec a et b entiers, b étant
avec a et b entiers, b étant chacune des inéquations suivantes et donner l’ensemble des solutions à l’aide d’un
chacune des inéquations suivantes et donner l’ensemble des solutions à l’aide d’un



