Problèmes ouverts de maths à résoudre et à télécharger en PDF.

Problèmes ouverts : cette notion de maths à résoudre et à télécharger en PDF.

La série de ces problèmes ouverts de maths afin de réfléchir sur des exercices complexes avec un travail individuel ou en groupe.Ces exercices développent l’esprit d’initiative et le raisonnement scientifique pour les élèves du collège et du lycée.

Puis une série d’exercices  afin de développer la prise d’initiative et le raisonnement scientifique chez l’élève ou chez l’internaute.Faites travailler votre matière grise en essayant de résoudre ces différents énoncés.

De plus, le socle est l’ensemble des connaissances et compétences que tout élève doit avoir acquis en fin de collège et qui seront validées dans le livret personnel de compétences (L.P.C) en trois paliers.

Ces nombreux cette méthode de maths  et tâches complexes , vous permettront d’évaluer de nombreuses compétences et permettront également, aux élèves d’entamer une démarche scientifique et de favoriser la prise d’initiative.

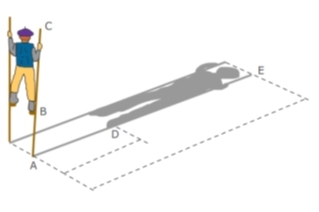
L’ombre (Problèmes ouverts)

On suppose que les rayons du soleil sont parallèles. AB = 120 cm ; AD = 210 cm ; AE = 518 cm. Calculer BC

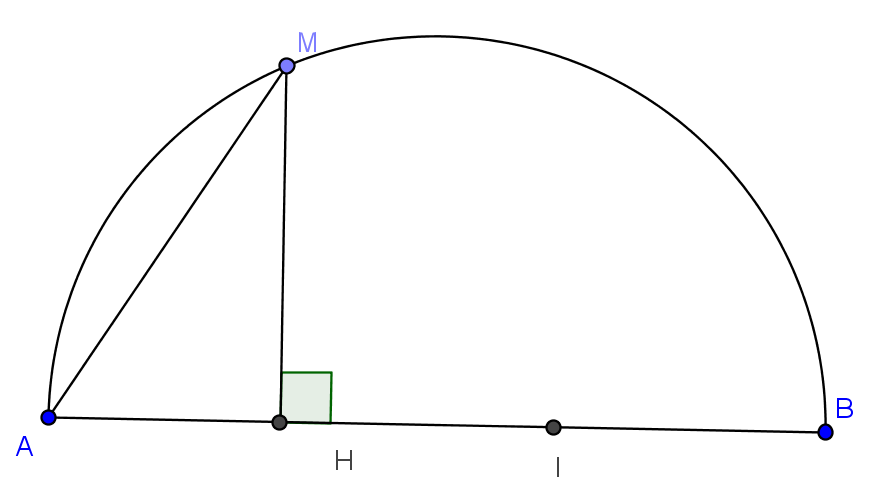
Moyenne géométrique et arithmétique

On considère un demi-cercle de diamètre [AB].

M est un point quelconque sur le demi-cercle et le point H est sa projection orthogonale sur [AB].

Ensuite, le point I est le milieu de [HB].

Par ailleurs, montrer que AI > AM.

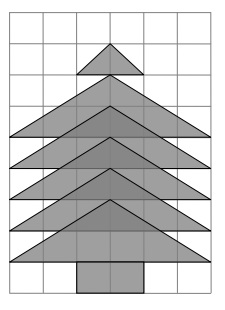
LE SAPIN (Problèmes ouverts)

Un sapin est dessiné sur une feuille de papier quadrillé : le tronc est un rectangle formé de deux carrés, alors que le reste
du sapin est formé de cinq triangles égaux, partiellement superposés, et d’un triangle plus petit qui constitue la pointe.
Marie observe le dessin et est convaincue que la partie de la feuille occupée par le sapin est plus grande que celle qui reste.
Pensez-vous que Marie a raison ?

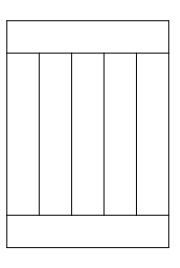
LA TABLE DE JARDIN

Le papa de Luc a construit une table de jardin rectangulaire en utilisant 7 planches de bois identiques, ayant chacune un périmètre de 3 m.
Voici le dessin du plateau de la table, comme il se présente à la fin de la construction.

De plus, quelle est la longueur et la largeur de cette table  de jardin ?

LES BANCS DU PARC (Problèmes ouverts)

Dans un grand parc, il y a deux sortes de bancs : des bancs à deux places et des bancs à trois places.
Puis il y a 15 bancs à deux places de plus que de bancs à trois places.
Ensuite, il y a en tout 185 places assises sur les bancs du parc.
Par ailleurs, combien ce parc compte-t-il de bancs en tout ?

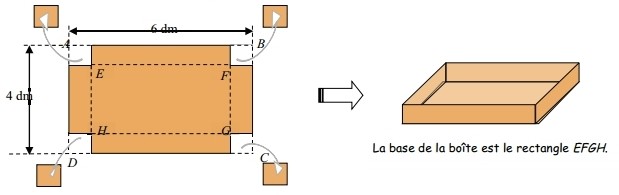
Patrons de récipients

Dans une fabrique de boîtes en carton on dispose de plaques rectangulaires de longueur 6 dm et de largeur 4 dm.

Avec de telles plaques on veut fabriquer des boîtes sans couvercle dont la forme est un  pavé dont le volume est  .
Puis pour cela on découpe, dans chaque plaque, quatre carrés identiques.

Problème :Déterminer la longueur des côtés des carrés à découper ?

L’âge du professeur (Problèmes ouverts)

Le professeur de mathématiques propose à ses élèves une question subtile :
Enfin, calculez mon âge sachant que :

si je double l’âge que j’aurai dans 4 ans et si j’enlève 20 à l’âge que j’avais il y a 4 ans, la
différence entre les deux nombres obtenus est le double de l’âge que j’ai aujourd’hui !

À vous maintenant de trouver mon âge !

De même, quel est l’âge du professeur ?

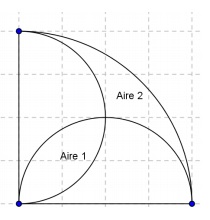
Surface à peindre

Deux peintres Yoann et Benoit doivent peindre une fresque.
Yoann doit peindre la surface Aire1.
Benoit  peint la surface Aire 2.
Également, quel est celui qui a la plus grande surface à peindre ?

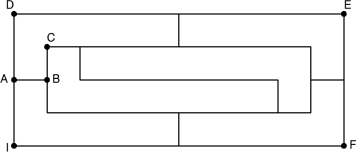
LA LONGUEUR DU DÉFI (Problèmes ouverts)

Un terrain rectangulaire DEFI est partagé en six parcelles de même forme et de même aire.

Sur le plan ci-dessous, la disposition des parcelles est respectée, mais les distances et les proportions ne sont pas justes.

Ensuite, on sait seulement que AB = BC = 1.

LE CHAMP DU PÈRE MÉABLE : problème ouvert

Pierre Méable possède un champ carré de 100.

DÉFENSE D’Y VOIR (Problèmes ouverts)

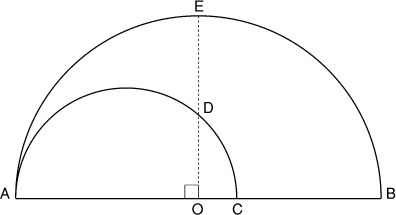
Une défense d’éléphant est représentée ci-dessous par deux demi-cercles tangents en A et centrés sur (AB), le point O étant le centre du grand demi-cercle.

De plus, on sait que OA = 9 dm et DE = 3 dm.

Ensuite, déterminez la longueur AC.

DES POMMES ET DES POIRES

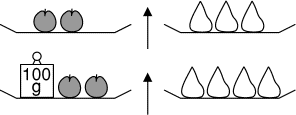
Puis les pommes ont toutes la même masse et les poires ont toutes la même masse.
De plus, quelle est la masse d’une pomme?

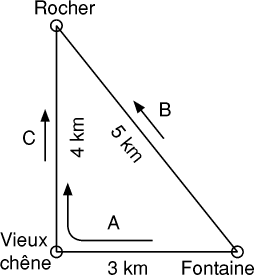
LES TROIS RANDONNEURS (Problèmes ouverts)

Trois randonneurs se déplacent sur le circuit pédestre représenté ci-contre, chacun marchant toujours dans le même sens, comme indiqué sur la figure, et à vitesse constante. Albert et Béatrice marchent à la même vitesse, tandis que Camille marche deux fois plus vite. Albert et Béatrice sont partis à 10 heures de la fontaine, et Camille à 11 heures du vieux chêne, juste au moment où Albert y passait.
À quelle heure Béatrice et Camille se rencontreront-elles pour la première fois?

L’HÉRITAGE EST DANS LE LAC

LE DIAMANT (Problèmes ouverts)

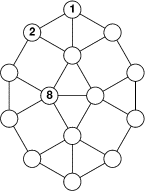
Par ailleurs, les cercles de ce diamant doivent contenir les nombres de 1 à 14, de telle sorte que la différence entre deux nombres reliés par un segment, prise en valeur absolue,

• soit toujours un nombre inférieur ou égal à 5
• ne soit jamais égale à 3.

Complétez le diamant.

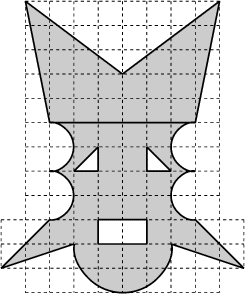
LE MASQUE AZTÈQUE

Des fouilles récentes ont permis de mettre à jour un masque aztèque en or pur. Par ailleurs, le plan de ce masque est représenté ci-dessous.

Enfin, calculez l’aire de ce masque, l’unité d’aire étant l’aire d’un petit carré. Puis on n’oubliera pas de déduire l’aire des yeux et de la bouche.
Ensuite, pour d’éventuels calculs, on prendra 3,14 pour pi.

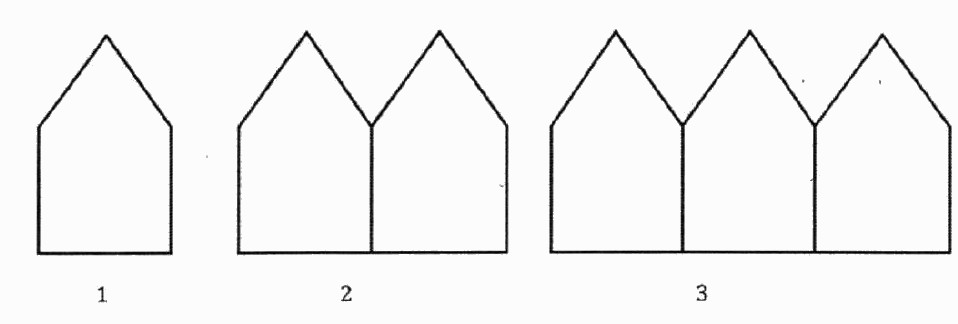
LA FRISE QUI DÉFRISE (Problèmes ouverts)

Thomas a découpé quarante formes identiques à celle représentée ci-dessous.

De même, il a commencé à les assembler en une frise régulière.

Lorsqu’il aura fini de poser la 40^ème forme, quel sera le périmètre de la frise ainsi formée?

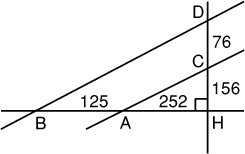
LES FOURMIS GÉOMÈTRES

Deux fourmis se rencontrent au point H.
1 ^ère fourmi:  De B à A il y a 125 unités (de longueur fourmi), et de A à H, il y en a 252 .
2 ^ème fourmi:  De D à C il y a 76 unités, et de C à H, il y en a 156. De plus, (AB) est perpendiculaire à (CD).
1 ^ère fourmi:  (BD) et (AC) semblent parallèles.
2 ^ème fourmi:  Certainement pas, car l’entrée de ma fourmilière se trouve à l’intersection de ces deux pistes!
1 ^ère fourmi:  Je me suis trompée, mais ta fourmilière doit être bien loin…
Puis calculez la distance à vol d’oiseau de la fourmilière de la seconde fourmi à la piste (AB). De plus, on donnera la réponse en unités-fourmi.

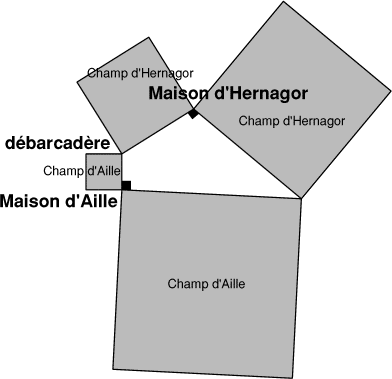
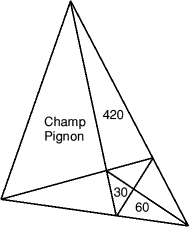
LE CHAMP PIGNON ET LES PRÉS D’ILEXION (Problèmes ouverts)

Dans la commune rurale de Triangle, le cadastre ne comporte que des parcelles triangulaires (voir extrait de ce cadastre ci-dessous).

Monsieur Ilexion possède trois parcelles dont il connaît bien les superficies, qui sont respectivement égales à 420 m², 30 m², et 60 m².

Mais quelle est donc la superficie du Champ Pignon?

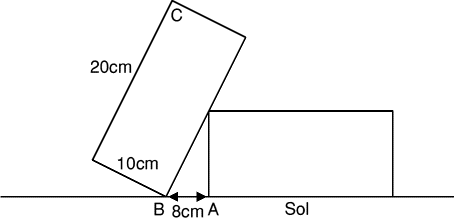
Les briques :

Deux briques identiques (dimensions en projection 20 cm × 10 cm) sont disposées comme indiqué sur le dessin.
Ensuite, la distance AB est 8 cm.

A quelle distance du sol est le point C?

Maisons et allumettes (Problèmes ouverts)

Également, combien d’allumettes sont nécessaires pour construire ces maisons à l’étape 5 ? 16 ? 256 ?

Ensuite, combien d’étapes  peut-on effectuer avec 1 465 allumettes ?

Madame Tymar et sa piscine :

Madame Tymar décide d’implanter une piscine enterrée dans son jardin.

Voici une vue de dessus de son bassin :

Pour des raisons de sécurité, elle veut recouvrir la piscine d’une bâche.
Par ailleurs, un commercial lui propose deux tarifs :

                     – Tarif A : 3€ le m² de bâche et 150€ de pose;

                     – Tarif B : un forfait bâche+pose à 399€.

Il indique à sa cliente que pour la fixation, la surface de bâche doit être de 10% supérieure à celle de la piscine.

Problématique : quel tarif sera le plus avantageux pour madame Tymar?

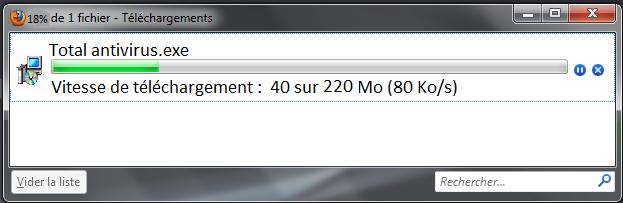
Temps de téléchargement (Problèmes ouverts)

Jean a lancé le téléchargement d’un antivirus gratuit sur internet : « Total antivirus ».

Au moment de partir faire son footing sur la promenade Pierre-Vernier, il peut voir la fenêtre ci-dessous :

Un terrain de tennis

Un terrain de tennis rectangulaire de 15 mètres sur 30 mètres est entouré d’une allée de largeur constante.
Puis le périmètre extérieur de cette allée est le double de celui du terrain de tennis.

Puis quelle est la largeur de cette allée ?

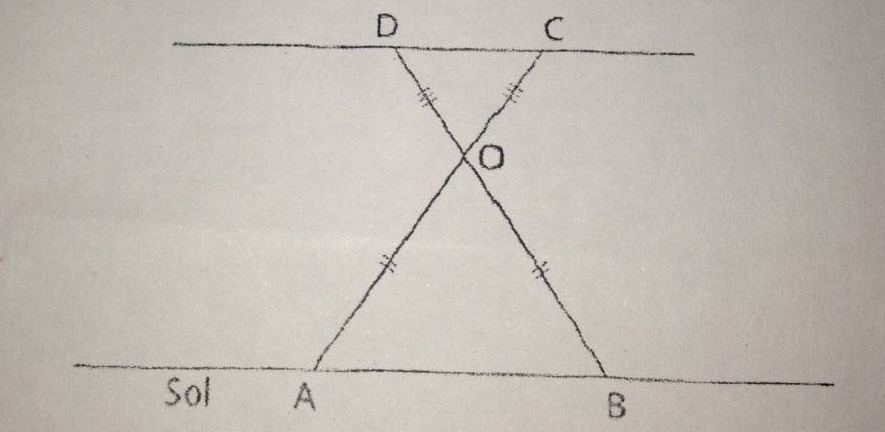
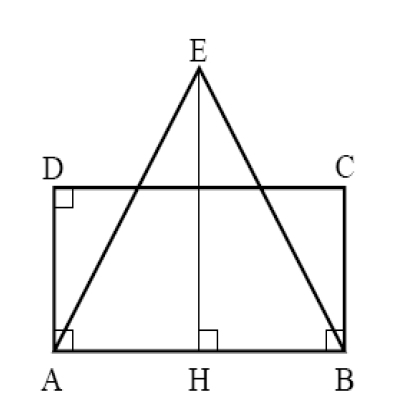
La table à repasser (Problèmes ouverts)

La hauteur d’une table à repasser peut se régler en ouvrant, plus ou moins, l’angle que forme ses pieds.

De plus, quelle que soit sa hauteur, la table restera alors toujours parallèle au sol.

Par ailleurs, comment est-ce-possible ?

Ensuite, la figure suivante va nous aider à le savoir.

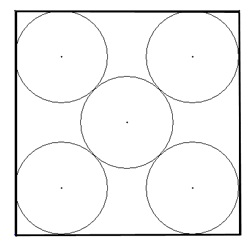
Les bouteilles

Dans une caisse carrée de 10 cm de côté, on a disposé 5 bouteilles identiques qui rentrent juste  dans la caisse comme le montre le dessin ci-dessous.

Enfin, quel est le diamètre des bouteilles?

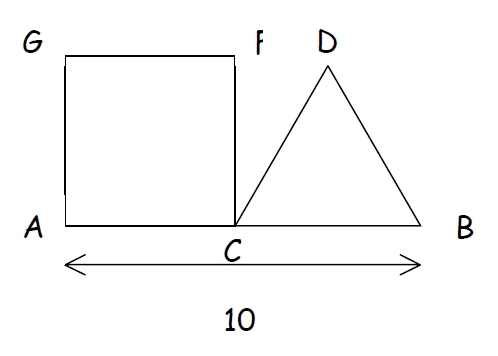
Calcul littéral (Problèmes ouverts)

Le carré ACFG et le triangle équilatéral BDC ont le même périmètre.
De même, quelle est la mesure d’un côté du triangle ?

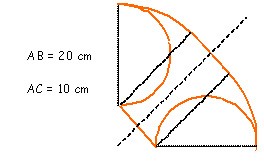
Léonard et l´arbalète

Léonard de Vinci au 15ème siècle s’est intéressé aux lunules.Il a complété la « collection » commencée par Hippocrate (au 5ème siècle avant J.C).

Parmi les 172 lunules qu’il a décrites et dessinées, l’une pourrait s’appeler l’arbalète de Léonard .

Puis nous vous donnons son dessin, ses dimensions principales et des éléments de sa construction.

1. De plus, un cercle de diamètre [AB].

2. Ensuite, un cercle de rayon [AB] et de centre A.

3. Par ailleurs, un angle de 45°.

4. Puis un rectangle de largeur AC et de longueur AB.

5. Ensuite, une symétrie axiale.

Calculer l’aire de l’arbalète de Léonard.

La bouteille (Problèmes ouverts)

La bouteille dessinée ci-contre est remplie d’eau à la moitié de sa capacité totale.

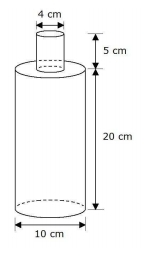
Également, quelle hauteur en cm, atteint le liquide ?

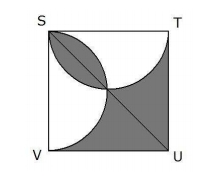
Géométriquement fleurie

Un part terre de fleurs a la forme d’un carré STUV de 2m de côté.
Man Jardin’tou, décide de planter des hibiscus dans la partie  grisée, qui est obtenu à partir des deux demi-cercle de diamètre [ST] et [SV].

Ensuite, quelle est l’aire de la région où Man Jardin’tou, va planter les hibiscus ?

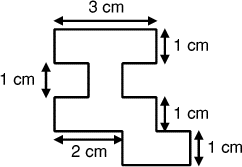
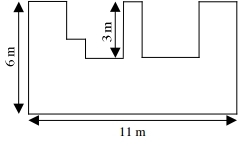
Calculer le périmètre d’une figure (Problèmes ouverts)

Calculer le périmètre de cette figure en utilisant les dimensions données.

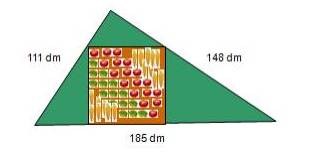
Le carré de légumes

Le terrain de Michao est triangulaire et ses dimensions sont 111 dm, 148 dm et 185 dm. Puis il a donc la forme
d’un triangle rectangle comme vous pouvez le vérifier par le calcul. Michao sait qu’il est possible d’y
implanter un potager de forme carré comme indiqué sur la figure ci-contre (un sommet sur chaque côté de
l’angle droit et deux sommets sur l’hypoténuse) mais il voudrait connaître l’aire du potager ainsi obtenu.

Pouvez-vous l’aider à la déterminer ?

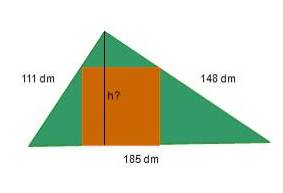
Michel, l’ami jardinier de Michao, lui a conseillé de calculer, pour commencer, la hauteur h issue du sommet de l’angle droit de son terrain.

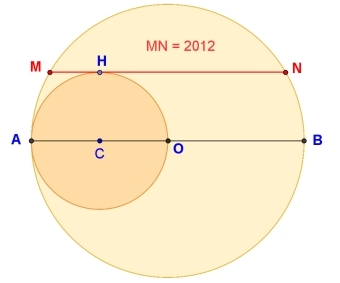
La corde (Problèmes ouverts)

Le point O est le milieu du segment [AB] et le point C le milieu du segment [AO].
De plus, la droite (MN) est parallèle à la droite (AB) et tangente en H au cercle de centre C et de rayon CO.
Ensuite, on donne MN = 2 012.
Par ailleurs, calculer le rayon du grand cercle et arrondir le résultat à l’unité la plus proche.

Fraction d’un carré

Mesure du côté d’un triangle (Problèmes ouverts)

Aire d’un carré :

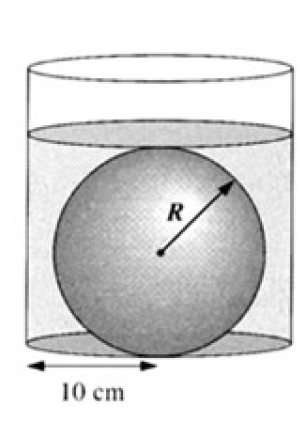
La boule immergée (lycée) (Problèmes ouverts)

On désire calculer le rayon R d’une bille d’acier en la déposant au fond d’un récipient cylindrique de 10 cm de rayon,
et en y versant un volume V d’huile, jusqu’au recouvrement de la bille.
Puis la surface libre de l’huile affleure alors le sommet de la bille.
Ensuite, la hauteur du récipient dépasse 20 cm.
Puis quel doit être le rayon R pour que V soit égal à  ?

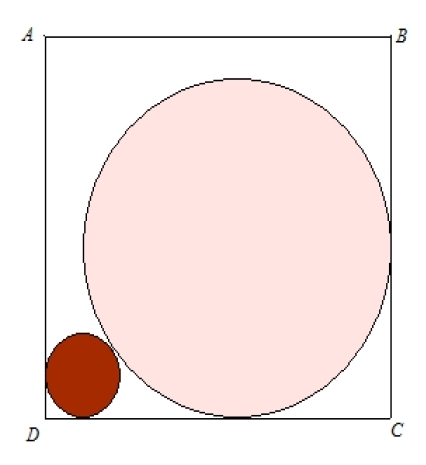
La boule et le cochonnet (lycée)

Le rayon de la boule est quatre fois celui du cochonnet.
Puis ils sont placés dans une boîte de 27 cm de côté.
De plus, quels sont leurs rayons ?

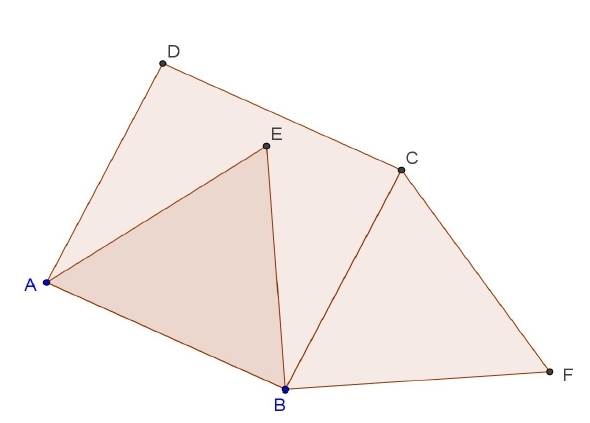
Des points alignés (lycée) (Problèmes ouverts)

ABCD est un carré, AEB et BCF sont équilatéraux.
De plus, les points D, E et F sont-ils alignés ?

Deux polygones (lycée)

La figure ci-contre représente un rectangle ABCD et un triangle isocèle ABE ayant tous les deux 12 cm de périmètre.
Ensuite, déterminer lequel de ces deux polygones a la plus grande aire suivant la valeur de AB.

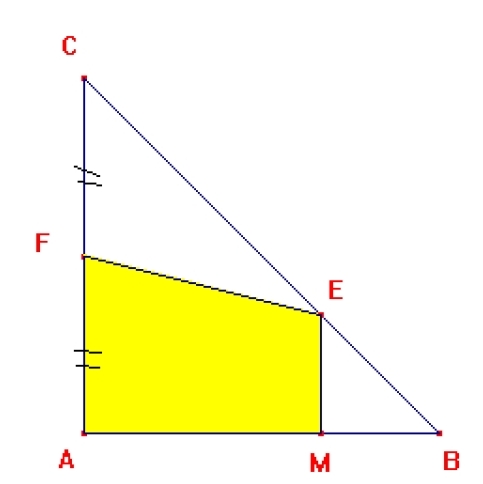
Aire maximale (lycée) (Problèmes ouverts)

On considère un triangle ABC isocèle et rectangle en A tel que AB=5 cm.
Soit F le milieu de [AC].

Soit (d) la perpendiculaire à (AB) issue de M, elle coupe (BC) en E.
Par ailleurs, on s’intéresse à l’aire du polygone EFAM.
Puis le but de la recherche est de trouver la position du point M sur [AB] pour laquelle l’aire est maximale.

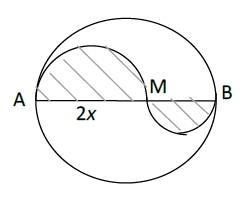
Le yin et yang (lycée)

Sur un diamètre [AB] d’un cercle de rayon 4 cm, on marque un point M.

Ensuite, on désigne par , avec  , la longueur de AM.
Puis on trace deux demi-cercles de part et d’autre de (AB), de diamètre [AM] pour l’un et [BM] pour l’autre.
De plus, exprimer l’aire de la partie hachurée et déterminer pour quelle valeur de x cette aire est maximum.

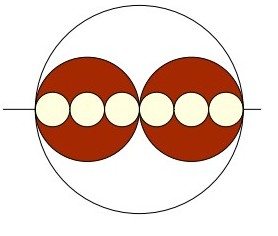
Fractions de disques (Problèmes ouverts)

1. A quelle fraction du grand disque correspondent les six petits disques ?
2. A quelle fraction du grand disque correspond l’aire en marron ?

La ficelle et les deux carrés (lycée)

On coupe une ficelle de 32 cm de long en 2 morceaux avec lesquels on forme 2 carrés.
Où doit-on couper la ficelle pour que la somme des aires des 2 carrés soit la plus petite possible ?

Evaporation d’un liquide (lycée) (Problèmes ouverts)

Dans un laboratoire, pour étudier l’évaporation d’un liquide, le professeur Holè est chargé de mesurer chaque jour la
hauteur de ce liquide dans un tube à essai.
Ensuite, il commence le lundi (jour 1) et mesure une hauteur de 8,2cm.
Par ailleurs, le lendemain, la hauteur du liquide est de 7,6cm.
M. Holè oublie de faire le relevé le mercredi.
Puis il s’en rend compte le jeudi, la hauteur du liquide est alors de 6,4 cm.
Au bout de combien de jour n’y aura-t-il plus de liquide ?

Problème de la fourmi (lycée)

Une fourmi se déplace le long des arêtes d’un cube.
Si elle se rend d’un sommet au sommet opposé sans passer deux fois par le même point,
quelle est la longueur maximale de son trajet ?
Ensuite, une fourmi ( M ) cherche à rejoindre un morceau de sucre ( S ) par le chemin le plus court. (la fourmis trouve

toujours le chemin le plus court ! Et vous ?)

Construction d’une boîte (lycée) (Problèmes ouverts)

Voici, en gras, le patron d’une boite sans couvercle découpé dans une feuille cartonnée.
Objectif 1: Construire à l’aide d’une feuille identique la boite ayant le plus grand volume !
Objectif 2: Construire à l’aide d’une feuille identique la boite la plus légère !

Gardien d’une propriété (lycée) :

Un gardien est chargé de la surveillance d’une propriété rectangulaire de 5 hm sur 4 hm. Puis il dispose d’un talkie-walkie.
pour communiquer avec un autre gardien situé à l’intérieur de la propriété.
De plus, la qualité de la communication dépend de la distance entre les deux gardiens.
Ensuite, le schéma ci dessous illustre cette situation :
Par ailleurs, on note M la position du premier gardien qui se déplace à partir du point A en direction du point B jusqu’à compléter le tour de la propriété.
Par ailleurs, le point O symbolise le deuxième gardien.
Puis les dimensions sont indiquées sur le dessin.
.

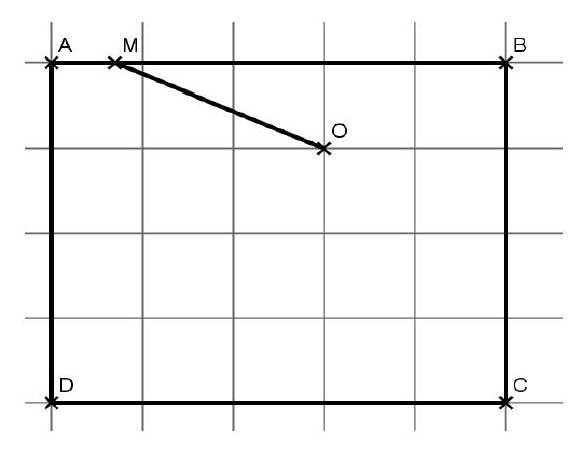
Décrire l’évolution de la distance OM selon la distance parcourue par le gardien.

Parc et pont (lycée) (Problèmes ouverts)

ABCD est un parc carré de côté 10 mètres.

Ensuite, il passe un cours d’eau de largeur 1 mètre à travers ce parc, matérialisé par le rectangle EFGH avec AE = 6 mètres.

Où franchir le pont pour que le trajet de A à C soit le plus court possible ?

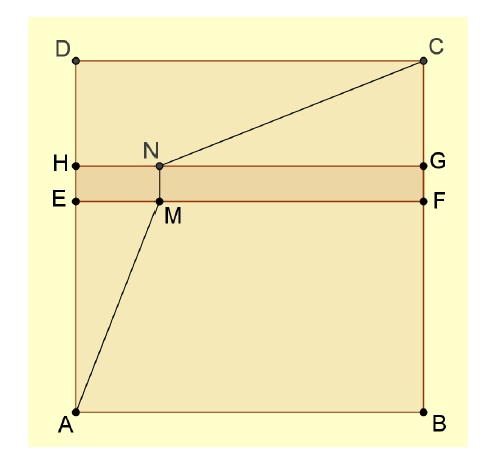
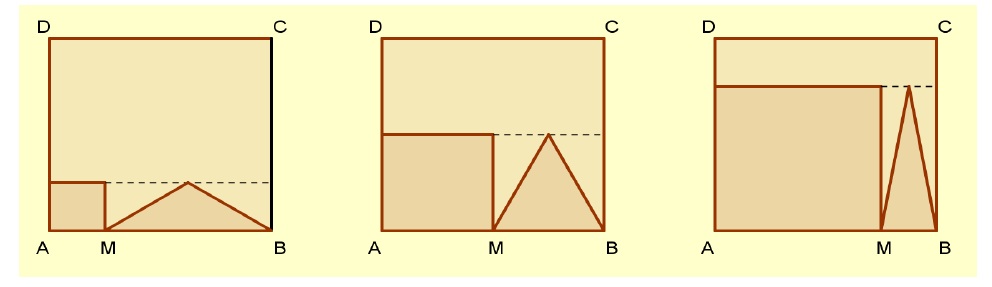
Carré et aire (lycée) :

Le carré ABCD a un côté de longueur 8 cm.
M est un point du segment [AB].
Puis on dessine dans le carré ABCD :
– Un carré de côté [AM]
– Un triangle isocèle de base [MB] et dont la hauteur a même mesure que le côté [AM] du carré.
Trois dessins sont proposés pour trois positions différentes du point M.

à partir de cette situation, plusieurs problèmes:

– Problème 1: Dans quelle situation a-t-on l’aire du triangle la plus grande ?
– Problème 2: Dans quelle situation l’aire du carré est égale à celle du triangle ?
– Problème 3: Dans quelle situation l’aire du motif est elle égale à la moitié de celle de ABCD ?
– Problème 4: Dans quelle situation a-t-on l’aire du triangle supérieure à la moitié de celle du carré ?
– Problème 5: Comment évolue l’aire du motif en fonction de AM ? en fonction de MB ?

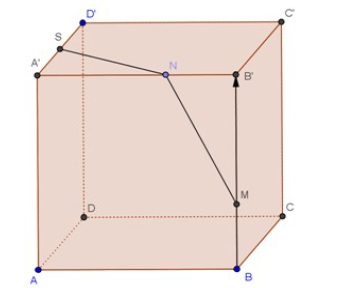
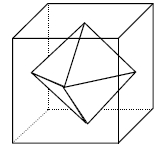
UN DIAMANT POUR GUINNESS (Problèmes ouverts)

Un précieux diamant de dimensions et d’une brillance
exceptionnelles est exposé dans le musée LUX.
De plus, pour le protéger, on a construit une boîte de verre en forme de
cube de 10 cm d’arête qui le contient exactement, de façon à ce
que chaque sommet du diamant soit au centre d’une face.
Ensuite, pour proposer ce diamant au « Guinness », il faut donner son
volume.

Par ailleurs, calculez son volume (en ).

Donc le volume du polyèdre est le 1/6 du volume du cube :
V= 1000/6 = 500/3 ≈167 (in cm3).

FACTORIELLES :

Anne, Berthe et Claire observent ce tableau de nombres, découvert dans les dernières pages d’un
vieux manuel de mathématiques :

1! = 1
2! = 1 x 2 = 2
3! = 1 x 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 24
5! = 1 x 2 x 3 x 4 x 5 = 120
6! = 1 x 2 x 3 x 4 x 5 x 6 = 720
7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 5 040
8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40 320
9! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 = 362 880

10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3 628 800
11! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 = 39 916 800
12! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 = 479 001 600
13! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 = 6 227 020 800
14! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 = 87 178 291 200
…

FACTORIELLES : (suite)

Anna dit : selon moi, le dernier nombre de la ligne 22! se terminera par quatre zéros.
Berthe dit : selon moi le dernier nombre de la ligne 27! se terminera par cinq zéros.
Claire dit : non, selon moi, le dernier nombre de la ligne 27! se terminera par six zéros.

Et vous, qu’en pensez-vous ?
Dites si les affirmations de chacune des trois amies sont vraies ou fausses, et pourquoi.

Puis il y a 6 facteurs 5, d’où 6 chiffres 0 en fin de 27!

LE CHAMP DE GRAND-PERE :

Un grand père offre à ses cinq petits-enfants un champ de
forme carrée divisé en cinq parcelles, un carré et quatre
triangles, telles que la longueur des côtés du carré situé au
centre est égale à celle des petits côtés de chacun des quatre
triangles. (Voir figure ci-dessous)

Indication :

Selon vous, les cinq parcelles ont-elles la même aire ?

BALLON DE FOOTBALL :

Un ballon de football est formé de 12 pentagones réguliers et de 20
hexagones réguliers maintenus entre eux par des coutures.
Leurs côtés mesurent tous 4,5 cm.

Enfin, quelle est la longueur totale des coutures ?
longueur de la couture : 90 x 4,5 cm, soit 405 cm

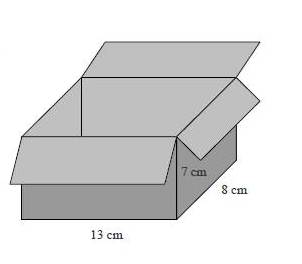
LA BOÎTE DE CUBES :

François a une boîte en forme de parallélépipède rectangle de
dimensions intérieures 13 cm, 8 cm et 7 cm.
Ensuite, il dispose de nombreux cubes en bois,
les uns de 2 cm d’arête, les autres de 1 cm d’arête.
François veut remplir complètement la boîte avec le moins
possible de cubes.

De même, combien doit-il en mettre de chaque sorte ?

BISCUITS :

Voici les biscuits que le pâtissier a préparés pour cinq enfants et qu’il a placés très précisément sur
un plateau.
Puis les biscuits sont tous de même épaisseur, mais certains enfants sont mécontents et disent que leur
biscuit est plus petit que celui des autres.

Pensez-vous que tous les enfants auront la même quantité de biscuit à manger ?
Sinon, mettez les biscuits dans l’ordre, du plus petit au plus grand.

LES POTS DE BONBONS :

Dans un premier pot, Grand-mère met 6 bonbons à l’orange
et 10 au citron.
De plus, dans un deuxième pot, elle met 8 bonbons à l’orange et 14 au
citron.
Ensuite, les bonbons sont de même forme et enveloppés de la même
façon.
Comme Grand-mère sait que Julien n’aime pas le goût du
citron, elle lui dit :
Également, tu peux prendre un bonbon. Je te laisse choisir le pot dans
lequel tu pourras glisser ta main, sans regarder à l’intérieur.

Julien réfléchit bien et choisit enfin le pot où il pense avoir la meilleure chance de prendre un
bonbon à l’orange.

À la place de Julien, quel pot auriez-vous choisi ?

À LA FONTAINE :

Deux amies, Laure et Pauline, vont chercher de l’eau avec un seau à la fontaine Eauclaire.
Leurs deux seaux contiennent ensemble 26 litres.
Avec l’’eau contenue dans le seau de Laure on peut remplir 3 fois le seau de Pauline
et il reste encore 2 litres d’eau dans le seau de Laure.

Ensuite, combien de litres contient le seau de Pauline ? Et celui de Laure ?

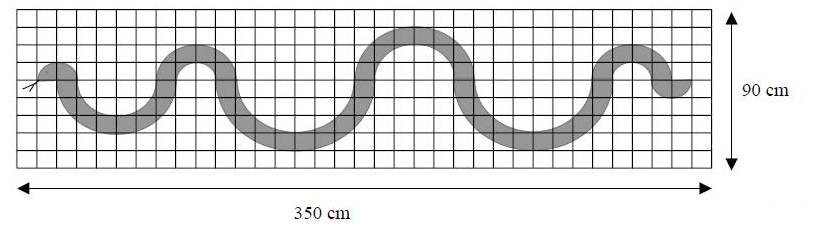
LE RESTAURANT CHINOIS :

L’enseigne du restaurant chinois « Le serpent rouge » est un long serpent rouge à l’intérieur d’un
rectangle doré.
Par ailleurs, cette figure est une reproduction fidèle de l’enseigne :

Puis quelle est la mesure de l’aire du serpent ?

PROFESSEUR TOURNESOL :

M. Tournesol se rend en voiture de sa maison à son bureau.
C’est seulement lorsqu’il est exactement à mi-chemin qu’il se rend compte que la petite lampe du niveau d’essence clignote et que son réservoir est presque vide.
Puis il décide alors de faire demi-tour pour se rendre à la station d’essence qui se situe exactement au
milieu du trajet déjà parcouru.
Après avoir fait le plein, il repart en direction de son bureau. Lorsqu’il y arrive, il constate que
son compteur indique 24 km.

Ensuite, il l’avait remis à zéro le matin en partant de sa maison.

A quelle distance de la maison se trouve le bureau de M. Tournesol ?

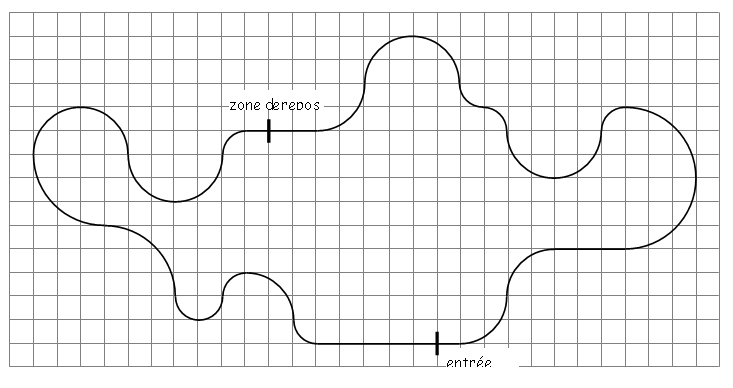
Le kartodrome

Ce que vous voyez représenté dans le dessin est le plan d’un circuit pour les courses du Go-Kart.

Lorsque le circuit n’est pas utilisé pour les compétitions, on peut s’y promener.

Luigi et Enrico veulent savoir s’il est plus avantageux de parcourir le circuit

dans le sens des aiguilles d’une montre ou en sens contraire pour rejoindre la zone de repos à partir de l’entrée.

Puis ils décident de marcher, à la même vitesse, en partant de l’entrée,

mais en allant dans les deux directions opposées,

Luigi dans le sens des aiguilles d’une montre, Enrico dans l’autre sens.

Qui arrivera le premier à la zone de repos ?

De plus, justifiez votre réponse et montrez vos calculs.

Le bouquet

Dans la classe de Sandra, les élèves apprécient beaucoup leur professeur de mathématiques. Ensuite, ils ont décidé de lui offrir un bouquet de fleurs pour la fête de Noël.

Chaque élève a donné autant de fois 2 centimes d’Euros qu’il y a d’élèves dans la classe.

Sandra a réuni les cotisations et fait le compte de ce qu’elle a reçu. Non compris sa propre contribution, elle a 22 euros et 44 centimes .

De plus, combien y a-t-il d’élèves dans la classe ?

Expliquez comment vous avez trouvé votre réponse.

Les factorielles

Anne, Berthe et Claire observent ce tableau de nombres, découvert dans les dernières pages d’un vieux manuel de mathématiques :

1! = 1

2! = 1 x 2 = 2

3!  = 1 x 2 x 3 = 6

4!  = 1 x 2 x 3 x 4 = 24

5! = 1 x 2 x 3 x 4 x 5 = 120

6! = 1 x 2 x 3 x 4 x 5 x 6 = 720

7! = 1 x 2 x 3 x 4 x 5 x 6 x 7= 5 040

8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40 320

9! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 = 362 880

10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3 628 800

11! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 = 39 916 800

12! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 = 479 001 600

13! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 = 6 227 020 800

14! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 = 87 178 291 200

…

Les factorielles (suite)

Anna dit : selon moi, le dernier nombre de la ligne 22! se terminera par quatre zéros.

Berthe dit : selon moi le dernier nombre de la ligne 27! se terminera par cinq zéros.

Claire dit : non, selon moi, le dernier nombre de la ligne 27! se terminera par six zéros.

Et vous, qu’en pensez-vous ?

Dites si les affirmations de chacune des trois amies sont vraies ou fausses, et pourquoi.

Le mot de passe

Marie-Thérèse Rococo a choisi un mot de passe pour son ordinateur, composé de 6 chiffres suivis de 3 lettres majuscules.

• les 6 chiffres choisis sont tous différents et le 0 ne figure pas parmi eux,

• leur somme est 23,

• les six chiffres forment un nombre inférieur à 420 000,

• le produit du premier chiffre et du dernier est 28,

• le troisième, le quatrième et le cinquième chiffres forment un nombre qui est multiple de 59,

• les trois lettres du code sont les initiales de Rococo Marie-Thérèse, dans cet ordre.

Par ailleurs, quel est le mot de passe de Marie-Thérèse ?

Expliquez votre raisonnement.

La machine à frites

Dans l’usine Bellefrites, on a installé plusieurs machines identiques pour couper les pommes de terre en frites.

Par ailleurs, le premier jour, on a fait fonctionner trois machines pendant deux heures et on a obtenu 300 kg de frites.

Puis le deuxième jour, on a fait fonctionner six machines pendant quatre heures.

Enfin, combien de kg de frites ont été obtenus au cours de ces deux jours ?

Expliquez comment vous avez trouvé la réponse.

Problèmes ouverts : méthode de travail

Tout d’abord, souligne les données utiles de chaque énoncé. Puis contrôle tes calculs avant de passer à la suite. Ainsi, tu repères vite tes erreurs de méthode. En outre, quelques minutes par jour suffisent pour retenir l’essentiel.

Par exemple, refais un exercice raté deux jours plus tard. Enfin, le programme officiel de mathématiques est détaillé sur le site Éduscol. Également, tu peux continuer avec tests de logique : entraînements sur des tests de QI.