Contrôles de maths

Des DM de maths en première S, ces devoir maison en 1ère S vous permettent de réviser au lycée ou de télécharger ces documents PDF afin de travailler à la maison et de réviser pendant les vacances scolaires.

Devoir maison en première S n°1

Corrigé du devoir maison en première S n°1

Devoir maison en première S n°2

Corrigé du devoir maison en première S n°2

Devoir maison en première S n°3

Corrigé du devoir maison en première S n°3

Devoir maison en première S n°4

Corrigé du devoir maison en première S n°4

Devoir maison en première S n°5

Corrigé du devoir maison en première S n°5

Devoir maison en première S n°6

Corrigé du devoir maison en première S n°6

Devoir maison en première S n°7

Corrigé du devoir maison en première S n°7

Devoir maison en première S n°8

Corrigé du devoir maison en première S n°8

Devoir maison en première S n°9

Corrigé du devoir maison en première S n°9

Devoir maison en première S n°10

Corrigé du devoir maison en première S n°10

Devoir maison en première S n°11

Corrigé du devoir maison en première S n°11

Devoir maison en première S n°12

Corrigé du devoir maison en première S n°12

Des DM sous forme de devoir maison de maths en troisième (3ème), ces devoir maison sont à effectuer en ligne ou à télécharger en PDF.Ces documents vous donnent la possibilité de travailler chez vous ou de réviser vos mathématiques pendant les vacances scolaires.

Ces Dm portant sur tous les chapitres de la classe de troisième :

1. l’arithmétique
2. le théorème de Thalès
3. la trigonométrie dans le triangle rectangle avec le cosinus, sinus et la tangente d’un angle aigu
4. le calcul littéral et les identités remarquables
5. les généralités sur les fonctions numériques
6. les racines carrées
7. les équations et inéquations du premier ordre et du premier degré
8. les statistiques
9. les systèmes de deux équations à deux inconnues
10. les sections de volumes dans l’espace avec les réductions et les agrandissements de solides
11. les probabilités

Devoir maison de maths en troisième – DM en 3ème n° 1

Devoir maison de maths en troisième – DM en 3ème n° 2

Devoir maison de maths en troisième – DM en 3ème n° 3

Devoir maison de maths en troisième – DM en 3ème n° 4

Devoir maison de maths en troisième – DM en 3ème n° 5

Devoir maison de maths en troisième – DM en 3ème n° 6

Devoir maison de maths en troisième – DM en 3ème n° 7

Devoir maison de maths en troisième – DM en 3ème n° 8

Devoir maison de maths en troisième – DM en 3ème n° 9

Devoir maison de maths en troisième – DM en 3ème n° 10

Devoir maison de maths en troisième – DM en 3ème n° 11

Devoir maison de maths en troisième – DM en 3ème n° 12

Devoir maison de maths en troisième – DM en 3ème n° 13

Ces sujets de devoir maison sont adressés autant aux élèves qu’aux professeurs de la classe de troisième au collège.

Des Dm et devoir maison de maths en quatrième (4ème), des devoirs à la maison sont en PDF et à effectuer en ligne au collège.

Ces DM portent sur tout le programme officiel de l’éducation nationale en mathématiques et les chapitres traités sont :

1. Les nombres relatifs
2. Le théorème de Pythagore
3. Les fractions et le calcul fractionnaire
4. Le truangle rectangle et le cercle circonscrit
5. Les puissances d’un nombre relatif et les puissances de 10
6. les propriétés de la droite des milieux dans un triangle et le théorème des parallèles (partie directe du théorème de Thalès)
7. Le calcul littéral et la double ditributivité
8. les statistiques
9. le cosinus d’un angle aigu dans un triangle rectangle
10. les équations à résoudre

Ces devoir maison vous permettent de vous exercer ou de réviser vos mathématiques pendant les vacances scolaires.

• Devoir maison de maths en quatrième (4ème) – DM n° 1
• Devoir maison de maths en quatrième (4ème) – DM n° 2
• Devoir maison de maths en quatrième (4ème) – DM n° 3
• Devoir maison de maths en quatrième (4ème) – DM n° 4
• Devoir maison de maths en quatrième (4ème) – DM n° 5
• Devoir maison de maths en quatrième (4ème) – DM n° 6
• Devoir maison de maths en quatrième (4ème) – DM n° 7
• Devoir maison de maths en quatrième (4ème) – DM n° 8
• Devoir maison de maths en quatrième (4ème) – DM n° 9
• Devoir maison de maths en quatrième (4ème) – DM n° 10

Un devoir maison sur les suites numérique et la démonstration par récurrence en terminale S.

Ce DM est à télécharger au format PDF pour les enseignants et pour les élèves de lycée en classe de terminale S.

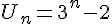Nous étudierons la suite (Un) définie par   et la suite (U_n) définie par .

Démontrer par récurrence une propriété puis calculer la limite d’une suite.

L’élève sera, également, amené à écrire un algorithme permettant de déterminer à partir de quel rang le terme un est strictement supérieur à un nombre réel A choisit par l’utilisateur.

Déterminer le sens de variation de la suite (un) puis conjecturer une expression de Un en fonction de n et démontrer par récurrence que cette expression est valable pour tout entier naturel n.

Le corrigé de ce devoir maison en terminale S peut être imprimé et téléchargé en PDF.

DM devoir maison sur les suites et le raisonnement par récurrence

Corrigé du DM devoir maison sur les suites et le raisonnement par récurrence

Une série de DM (devoir maison) en seconde afin d’effectuer ses devoirs à domicile.De nombreux DM sur tout le programme de mathématiques en classe de seconde.

Etoile sur l’écran d’une calculatrice

DM de l’étoile sur un écran de calculatrice

Corrigé du DM de l’étoile sur un écran de calculatrice

Fonctions et inéquations

DM sur les fonctions et inéquations en seconde

Corrigé du DM sur les fonctions et inéquations en 2de

Le prix moyen et les formules

DM sur le prix moyen et les volumes en 2de

Corrrigé du DM sur le prix moyen et les volumes en 2de

Fractions et formules

DM sur les fractions et formules en 2de

Corrigé du DM sur les fractions et formules et 2de

Volume d’une boîte et les fonctions

Dm sur le volume d’une boîte et les fonctions

Les fonctions et les coordonnées dans le plan

DM sur les fonctions et coordonnées en seconde

Un devoir maison de maths en troisième sur les équations et inéquations, le calcul littéral et l’arithmétique ainsi que le calcul avec les fractions et les puissances.

Ce Dm contient les savoirs faire suivants :

• Développe puis réduis D.
• Factorise D.
• Résous l’équation :  .
• ABCDEFGH est un cube d’arête [AB] avec AB = 12 cm.
  I est le milieu du segment [AB].
  J est le milieu du segment [AE].
  K est le milieu du segment [AD].
  a Calcule l’aire du triangle AKI.
  b Quel est le volume de la pyramide JAIK de base AIK ?
  c Quelle fraction du volume du cube représente le volume de la pyramide JAIK ?
• Résous les équations suivantes.
• Résous les inéquations suivantes.
• Les nombres 682 et 496 sont–ils premiers entre eux ? Justifie.
  Calcule le Plus Grand Commun Diviseur (PGCD) de 682 et 496.
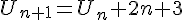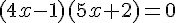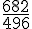  Simplifie la fraction   pour la rendre irréductible, en indiquant la méthode.
• Calcule A et B en donnant les étapes du calcul et écrire le résultat sous forme de fraction
  simplifiée.
• Donne l’écriture scientifique de C et D en détaillant les étapes du calcul conduisant au
  résultat.

Ce devoir maison de mathématiques en troisième est à télécharger en PDF pour les élèves et enseignants du collège en classe de troisième.

DM sur le calcul littéral, équations et inéquations et calculs en troisième