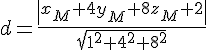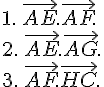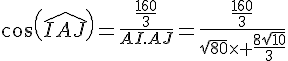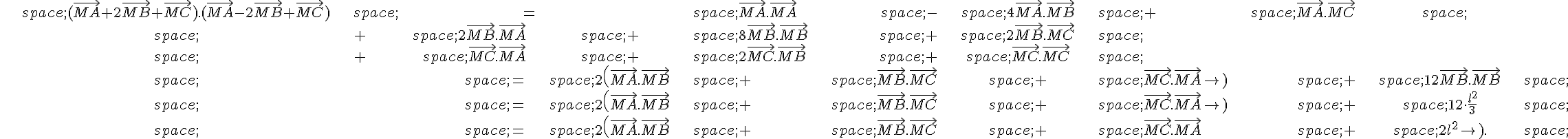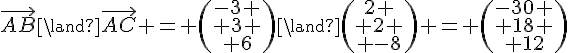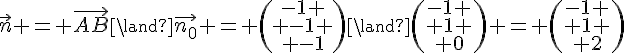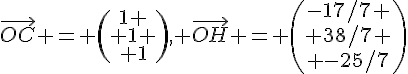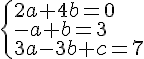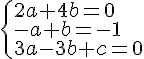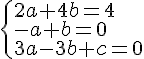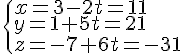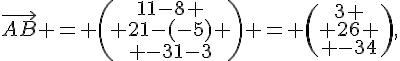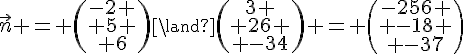Produit scalaire : corrigé des exercices de maths en terminale en PDF.

Mis à jour le 29 mai 2025

🔍Corrigés Détaillés

Terminale • Lycée

Produit scalaire

🔎 Analyse : 18 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en terminale sur le produit scalaire dans l’espace. Vecteurs colinéaires et orthogonaux et savoir déterminer l’équation d’une droite et d’un plan ainsi que, appliquer la relation de Chasles sur les vecteurs.

Exercice 1 :

Calculer la distance du point M(5; 2; −3) au plan d’équation x + 4y + 8z = −2.

La distance du point M au plan est donné par :

$d=\frac{ | x_M+4y_M+8z_M+2 |}{\sqrt{1^2+4^2+8^2}}$

$d=\frac{ | 5+4\times 2+8\times (-3)+2 |}{81}$

$d=\frac{ | 5+8-24+2 |}{81}$

$d=\frac{ | -9 |}{81}$

$d=\frac{9}{81}$

${\color{DarkRed} d=\frac{1}{9}}$

Exercice 2 :

Soient A(1; −1; 1), B(0; 2; −1) et C(−1; 1; 0).

Montrer que A, B et C forment un plan puis déterminer x aﬁn que $\vec{u}$ (x; 3; 4) soit normal à (ABC).

$\vec{AB}(-1;3;-2)$ et $\vec{AC}(-2;2;-1)$

Ces deux vecteurs ne sont pas colinéaires donc les points A,B et C forment un plan.

Un vecteur normal est

$\vec{AC}v \vec{AC}(1;3;4)$

il faut qu’il soit colinéaire à $\vec{u}$ , pour cela il suffit de prendre x = 1 .

Exercice 3 :

Les plans $P\,:\,2x\,-\,y\,+\,z\,+\,9\,=\,0$ et $Q\,:\,x\,+\,y\,-\,z\,-\,7\,=\,0$ sont-ils orthogonaux ?

Si les plans sont orthogonaux alors les vecteurs normaux sont orthogonaux.

$\vec{u}(2;-1;1)$ est un vecteur normal à (P).

$\vec{v}(1;1;-1)$ est un vecteur normal à (Q) .

$\vec{u}.\vec{v}=2\times 1-1\times 1+1\times (-1)=2-1-1=0$

Conclusion :

Le produit scalaire est nul donc ces deux plans sont orthogonaux.

Exercice 4 :

Déterminer une équation cartésienne du plan P passant par A(−2; 1; 3) et orthogonal
à (BC) où B(1; −2; 2) et C(4; 1; −1).

$\vec{BC}(3;3;-3)$ est un vecteur normal au plan (P).

Une équation cartésienne au plan (P) est du type :

or le point A appartient au plan (P) donc :

$3\times (-2)+3\times 1-3\times 3+d=0$

-12+d=0

d=12

Conclusion : une équation cartésienne de (P) est

Exercice 5 :

Déterminer une équation cartésienne du plan contenant A(2; −1; 1) et orthogonal au

vecteur $\vec{n}$ (3; −4; 2)

L’équation cartésienne est du type avec $\vec{n}$ un vecteur normal

donc nous avons déjà :

or A appartient à ce plan donc :

$3\times 2-4\times (-1)+2\times 1+d=0$

${\color{DarkRed} d=-12}$

Conclusion : l’équation cartésienne de ce plan est

Exercice 6 :

Le vecteur $\vec{n}$ (6; −2; 4) est-il normal au plan d’équation −3x + y − 3z = 1 ?

un vecteur normal au plan est $\vec{u}(-3;1;-3)$ or $\vec{u}$ et $\vec{n}$ ne sont pas colinéaires

donc $\vec{n}$ n’est pas un vecteur normal du plan.

Exercice 7 :

Déterminer un vecteur normal au plan d’équation 31x + 37y + 41z + 43 = 0.

D’après le cours un vecteur normal au plan est $\vec{u}(31;37;41)$ .

Exercice 8 :

On se place dans un repère orthonormal.

Soient A(−1; 1; 2), B(0; 1; 0) et C(2; 0; 3).

Calculer une mesure approchée de l’angle $\widehat{BAC}.$ .

$\vec{AB}(1;0;-2)$ et $\vec{AC}(3;-1;1)$ et $AB=\sqrt{1^2+0^2+(-2)^2}=\sqrt{5}$

et $AC=\sqrt{3^2+(-1)^2+1^2}=\sqrt{11}$

$\vec{AB}.\vec{AC}=1\times 3+0\times (-1)+(-2)\times 1=1$

$cos(\widehat{BAC})=\frac{\vec{AB}.\vec{AC}}{AB\times AC}=\frac{1}{\sqrt{5}\times \sqrt{11}}=\frac{1}{\sqrt{55}}$

${\color{DarkRed} \widehat{BAC}\simeq 82^{\circ}}$

Exercice 9 :

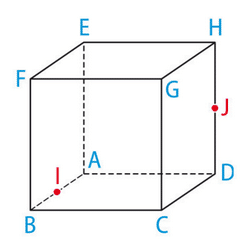
Soit ABCDEFGH un cube d’arête a.

Calculer :

$1.\,\vec{AE}.\vec{AF}.\\2.\,\vec{AE}.\vec{AG}.\\3.\,\vec{AF}.\vec{HC}.$

$\vec{AE}.\vec{AF}=a\times a\times cos \,\frac{ \pi } {4}=\frac{a^2\sqrt{2}}{2}$

Exercice 10 :

Soit ABCD un tétraèdre régulier d’arête a.

Calculer $\vec{AB}.\vec{AC}.$

$a^2\times cos (\frac{ \pi }{3} )$

Exercice 11 :

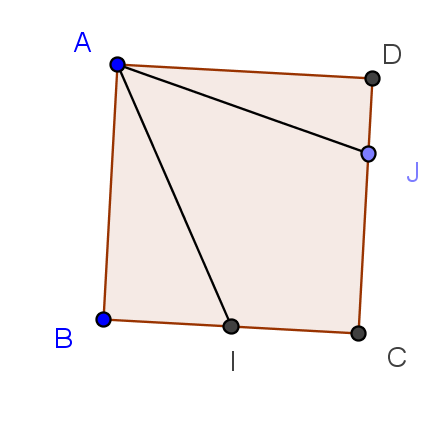
ABCD est un carré de coté 8 unités.

Les points I et J sont définis pas $\vec{BI}=\frac{1}{2}\vec{BC}$ et $\vec{DJ}=\frac{1}{3}\vec{DC}$ .

1. Exprimer le produit scalaire $\vec{AI}.\vec{AJ}$ de deux façons différentes .

$\vec{AI}.\vec{AJ}=(\vec{AB}+\vec{BI}). ( \vec{AD} +\vec{DJ} )$

$\vec{AI}.\vec{AJ}=\vec{AB}.\vec{AD}+\vec{AB}.\vec{DJ}+\vec{BI}.\vec{AD}+\vec{BI}.\vec{DJ}$

$\vec{AI}.\vec{AJ}=0+\vec{AB}.\vec{DJ}+\vec{BI}.\vec{AD}+0$

$\vec{AI}.\vec{AJ}=AB\times DJ+BI\times AD$

$\vec{AI}.\vec{AJ}=8\times \frac{8}{3}+4\times 8$

$\vec{AI}.\vec{AJ}=\frac{64}{3}+32$

$\vec{AI}.\vec{AJ}=\frac{64+96}{3}$

$\vec{AI}.\vec{AJ}=\frac{160}{3}$

2. Déterminer $cos(\widehat{IAJ})$ , puis la mesure de cet angle en radians .

$cos(\widehat{IAJ})=\frac{\vec{AI}.\vec{AJ}}{AI.AJ}=\frac{\frac{160}{3}}{AI.AJ}$

En utilisant le théorème de Pythagore :

$AI=\sqrt{8^2+4^2}=\sqrt{80}$ et $AJ=\sqrt{8^2+{(\frac{8}{3})}^2}=\sqrt{64+\frac{64}{9}}=\sqrt{\frac{640}{9}}=\frac{8\sqrt{10}}{3}$

$cos(\widehat{IAJ})=\frac{\frac{160}{3}}{AI.AJ}=\frac{\frac{160}{3}}{\sqrt{80}\times \frac{8\sqrt{10}}{3}}$

$cos(\widehat{IAJ})=\frac{\frac{160}{3}}{AI.AJ}=\frac{160}{8\sqrt{800}}$

$cos(\widehat{IAJ})=\frac{\frac{160}{3}}{AI.AJ}=\frac{160}{80\sqrt{8}}$

$cos(\widehat{IAJ})=\frac{\frac{160}{3}}{AI.AJ}=\frac{2}{\sqrt{8}}$

$cos(\widehat{IAJ})=\frac{\frac{160}{3}}{AI.AJ}=\frac{2\sqrt{8}}{8}$

$cos(\widehat{IAJ})=\frac{2\sqrt{2}}{4}$

$cos(\widehat{IAJ})=\frac{\sqrt{2}}{2}$

Conclusion :
${\color{DarkRed} \widehat{IAJ}=45^{\circ}}$

Exercice 12 :

On utilise la relation de Chasles : pour tout point , $\vec{AB} = \vec{AP} + \vec{PB}$ .

On a :
$\begin{align*}\,(\vec{MA}+2\vec{MB}+\vec{MC}).(\vec{MA}-2\vec{MB}+\vec{MC})\,=\,\vec{MA}.\vec{MA}\,-\,4\vec{MA}.\vec{MB}\,+\,\vec{MA}.\vec{MC}\,\\\,+\,2\vec{MB}.\vec{MA}\,+\,8\vec{MB}.\vec{MB}\,+\,2\vec{MB}.\vec{MC}\,\\\,+\,\vec{MC}.\vec{MA}\,+\,2\vec{MC}.\vec{MB}\,+\,\vec{MC}.\vec{MC}\,\\\,\,=\,2(\vec{MA}.\vec{MB}\,+\,\vec{MB}.\vec{MC}\,+\,\vec{MC}.\vec{MA})\,+\,12\vec{MB}.\vec{MB}\,\\\,\,=\,2(\vec{MA}.\vec{MB}\,+\,\vec{MB}.\vec{MC}\,+\,\vec{MC}.\vec{MA})\,+\,12\cdot\frac{l^2}{3}\,\\\,\,=\,2(\vec{MA}.\vec{MB}\,+\,\vec{MB}.\vec{MC}\,+\,\vec{MC}.\vec{MA}\,+\,2l^2).\,\end{align*}$

On pose $x = \vec{MA}.\vec{MB} + \vec{MB}.\vec{MC} + \vec{MC}.\vec{MA}$ . Alors l’équation devient soit : .

L’ensemble des points tels que cette équation est vérifiée est donc l’ensemble des points tels que $\vec{MA}.\vec{MB} + \vec{MB}.\vec{MC} + \vec{MC}.\vec{MA} = -l^2$ .

On note le centre du triangle équilatéral ABC . Alors pour tout point du plan, on peut écrire :

$\vec{MA}.\vec{MB}\,+\,\vec{MB}.\vec{MC}\,+\,\vec{MC}.\vec{MA}\,=\,\vec{OA}.\vec{OM}\,+\,\vec{OB}.\vec{OM}\,+\,\vec{OC}.\vec{OM}$

Si est à l’intérieur du triangle ABC , alors les produits scalaires sont positifs et on ne peut pas avoir $\vec{MA}.\vec{MB} + \vec{MB}.\vec{MC} + \vec{MC}.\vec{MA} = -l^2$ .

Si est sur le cercle circonscrit à ABC , on a $\vec{OA} + \vec{OB} + \vec{OC} = \vec{0}$ et en multipliant cette relation scalaire par $\vec{OM}$ , on obtient $\vec{OA}.\vec{OM} + \vec{OB}.\vec{OM} + \vec{OC}.\vec{OM} = 0$ ,

donc on peut avoir $\vec{MA}.\vec{MB} + \vec{MB}.\vec{MC} + \vec{MC}.\vec{MA} = -l^2$ .

Finalement, l’ensemble des points tels que $(\vec{MA}+2\vec{MB}+\vec{MC}).(\vec{MA}-2\vec{MB}+\vec{MC})=2l^2$ est précisément le cercle circonscrit à ABC ,

c’est-à-dire l’ensemble des points à distance du centre .

Exercice 21 :

Le module de $\vec{u}$ est donné par :

$||\vec{u}||=\sqrt{1^2+2^2+4^2}=\sqrt{21}$

Exercice 22 :

Le vecteur $\vec{AB}$ est donné par :

$\vec{AB}=(5-3;0-1;1-0)=(2;-1;1)$

Le module de $\vec{AB}$ est donc :

$||\vec{AB}||=\sqrt{2^2+(-1)^2+1^2}=\sqrt{6}$

Exercice 23 :

D’après la formule du parallélogramme, on a :

$4||\vec{u}||^2+||\vec{v}||^2-2||\vec{u}||\times ||\vec{v}||\times cos(\theta)=||\vec{v}-\vec{u}||^2 =\sqrt{5}^2=5$

En utilisant || $\vec{u}$ ||=1 et || $\vec{v}$ ||=2, on peut simplifier l’équation précédente :

$4+4-4cos(\theta)=5$

$\Rightarrow\,\,\,cos(\theta)=\frac{3}{4}$

En utilisant la définition du produit scalaire, on a :

$\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}||\times cos(\theta)=1\times 2\times \frac{3}{4}=\frac{3}{2}$

Exercice 24 :

On utilise la relation de la projection dans un triangle rectangle :

$\vec{AB}.\vec{AC}=AB.AC\times cos(\vec{BAC})$

$AB=\sqrt{5}$ et AC=8. De plus, on sait que le triangle BAC est rectangle en A et que $\widehat{ BAC} =60\,^{\circ}$ .

Donc, $cos(\widehat{ BAC} )=\frac{1}{2}$ .

On a donc :

$\vec{AB}.\vec{AC}=\sqrt{5}\times 8\times \frac{1}{2}=2\sqrt{5}$

Exercice 25 :

a) Le vecteur $\vec{AM}$ est la somme des vecteurs $\vec{AB}$ et $\vec{BM}$ , donc :

$\vec{AM}=\vec{AB}+\vec{BM}=\frac{a}{2}\vec{i}-\frac{a}{2}\vec{j}-\frac{a}{2}\vec{k}+\frac{a}{2}\vec{j}+\frac{a}{2}\vec{k}=\frac{a}{2}\vec{i}+\frac{a}{2}\vec{j}+\frac{a}{2}\vec{k}$

Donc, $||\vec{AM}||^2=(\frac{a}{2})^2+(\frac{a}{2})^2+(\frac{a}{2})^2=\frac{3}{2}a^2$ .

b) Le vecteur $\vec{AN}$ est la somme des vecteurs $\vec{AM}$ et $\vec{MN}$ , donc :

$\vec{AN}=\vec{AM}+\vec{MN}=\frac{a}{2}\vec{i}+\frac{a}{2}\vec{j}+\frac{a}{2}\vec{k}+\frac{a}{2}\vec{i}+\vec{k}=\frac{a}{2}\vec{i}+\frac{a}{2}\vec{j}+\frac{3}{2}a\vec{k}$

Donc, $||\vec{AN}||^2=(\frac{a}{2})^2+(\frac{a}{2})^2+(\frac{3}{2}a)^2=\frac{13}{4}a^2$ .

Le vecteur $\vec{MN}$ est la différence entre les vecteurs $\vec{BM}$ et $\vec{BN}$ , donc :

$\vec{MN}=\vec{BM}-\vec{BN}=\frac{a}{2}\vec{i}-\frac{a}{2}\vec{j}-\frac{a}{2}\vec{k}-(\frac{a}{2}\vec{i}+\frac{a}{2}\vec{j}+\frac{3}{2}a\vec{k})=-a\vec{j}-2a\vec{k}$

Donc, $||\vec{MN}||^2=a^2\times 0^2+(-a)^2+(-2a)^2=5a^2$ .

c) On sait que $\vec{AM}$ et $\vec{AN}$ sont orthogonaux car la diagonale AC d’un cube est perpendiculaire à chaque face, donc $\vec{AM}.\vec{AN}=0$ .

En développant cette expression, on a :

$\vec{AM}.\vec{AN}=(\frac{a}{2})^2+(\frac{a}{2})^2+(\frac{a}{2})^2+\frac{3}{2}a(\frac{a}{2})-\frac{a}{2}\times \frac{a}{2}-\frac{3}{2}a^2$

Exercice 26 :
a) $\vec{u}.\vec{v} = 2\times 1 + 3\times 0 + (-1)\times 2 = 0$
b) $\vec{u}.\vec{v} = 0 \times 6 + (-2)\times 1 + 5\times 1 = 3$
c) $\vec{u}.\vec{v} = 1\times 3 + (-1)\times (-1) + 2\times 1 = 6$

Exercice 27 :
1. Calculons les vecteurs $\vec{AB}$ et $\vec{AC}$ :
$\vec{AB} = (-2-1, 2-(-1), 6-0) = (-3,3,6)$
$\vec{AC} = (3-1,1-(-1),-8-0) = (2,2,-8)$
Ces vecteurs ne sont pas colinéaires, donc les points A,B,C ne sont pas alignés.
2.a) Calculons le produit scalaire de $\vec{n}$ avec $\vec{AB}$ et $\vec{AC}$ :
$\vec{n}.\vec{AB} = 3\times (-3) + 1\times 3 + 1\times 6 = 0$
$\vec{n}.\vec{AC} = 3\times 2 + 1\times 2 + 1\times (-8) = 0$

Les vecteurs $\vec{AB}$ et $\vec{AC}$ sont tous les deux orthogonaux à $\vec{n}$ , donc $\vec{n}$ est normal au plan (ABC).
b) Équation cartésienne du plan (ABC) :
Un vecteur normal au plan est donné par le produit vectoriel de $\vec{AB}$ et $\vec{AC}$ :
$\vec{AB}\land\vec{AC} = \begin{pmatrix}-3 \\ 3 \\ 6\end{pmatrix}\land\begin{pmatrix}2 \\ 2 \\ -8\end{pmatrix} = \begin{pmatrix}-30 \\ 18 \\ 12\end{pmatrix}$
Une équation cartésienne du plan est donc : avec d un réel quelconque.

Exercice 28 :
a) Un vecteur normal au plan \rho est donné par le produit vectoriel de $\vec{AB}$ et un vecteur normal à la droite (AB). Un vecteur directeur de (AB) est $\vec{AB} = (2-3, 1-2, -1-0) = (-1,-1,-1)$ , donc un vecteur normal à (AB) est par exemple $\vec{n_0} = (-1,1,0)$ (on pourrait aussi prendre $\vec{n_0} = (-1,0,1)$ ou (0,-1,1), en choisissant des coordonnées différentes pour $\vec{n_0}$ on obtiendra des équations de plans différentes mais toutes équivalentes). On a donc :
$\vec{n} = \vec{AB}\land\vec{n_0} = \begin{pmatrix}-1 \\ -1 \\ -1\end{pmatrix}\land\begin{pmatrix}-1 \\ 1 \\ 0\end{pmatrix} = \begin{pmatrix}-1 \\ 1 \\ 2\end{pmatrix}$
b) Équation cartésienne du plan $\rho$ :
Un point du plan $\rho$ est A, donc une équation cartésienne de $\rho$ est :

avec d un réel quelconque.

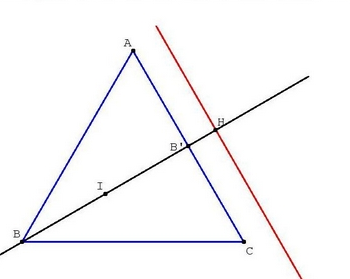
Exercice 29 :
1. Une représentation paramétrique de la droite (AB) est :
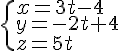
$\begin{cases}x = 3t-4 \\ y = -2t+4 \\ z = 5t\end{cases}$ avec $t\in\mathbb{R}$ .
2. On cherche à déterminer le point H de la droite (AB) qui minimise la distance CH.

Ce point est le projeté orthogonal de C sur (AB).

Soit H un point de (AB).

On a le triplet $(\vec{CH}).\vec{H} = 0$ , donc $((\vec{CH}.\vec{AB})/\|\vec{AB}\|^2)\vec{AB}.\vec{H} = \vec{CH}.\vec{H} = 0$ , d’où $\vec{CH}\land\vec{AB} = \vec{0}$ (les vecteurs $\vec{CH}$ et $\vec{AB}$ sont alors colinéaires).

On en déduit que H est le point d’intersection de (AB) et du plan passant par C et orthogonal à $\vec{AB}$ .
Une équation cartésienne de ce plan est :

, soit .

On résout le système d’équations suivant pour trouver H :

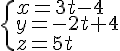
$\begin{cases}x=3t-4 \\ y=-2t+4 \\ z=5t\end{cases}$ et .

On trouve $t=-\frac{5}{7}$ puis $H = (-\frac{17}{7},\frac{38}{7},-\frac{25}{7})$ .
La distance CH est donnée par la norme du vecteur $\vec{CH} = \vec{OH}-\vec{OC}$ où O est l’origine du repère.

On a donc :
$\vec{OC} = \begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}, \vec{OH} = \begin{pmatrix}-17/7 \\ 38/7 \\ -25/7\end{pmatrix}$
et

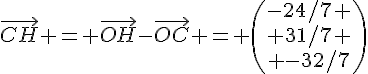
$\vec{CH} = \vec{OH}-\vec{OC} = \begin{pmatrix}-24/7 \\ 31/7 \\ -32/7\end{pmatrix}$ .
La distance CH est donc

$\|\vec{CH}\| = \sqrt{(-24/7)^2 + (31/7)^2 + (-32/7)^2} = \sqrt{1700}/7$ .

Exercice 30 :
1. Le vecteur $\vec{n}$ est orthogonal à toute combinaison linéaire de $\vec{u}$ et $\vec{v}$ , donc en particulier à leur produit vectoriel :
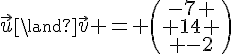
$\vec{u}\land\vec{v} = \begin{pmatrix}-7 \\ 14 \\ -2\end{pmatrix}$ .
$\vec{u}$ et $\vec{v}$ sont tous deux non nuls donc $\vec{u}\land\vec{v}$ est non nul, donc $\vec{n}$ est non nul.

De plus, on a $\vec{u}.\vec{v} = 2\times 4 -1\times 1 + 3\times (-3) = -6$ , donc le vecteur $\vec{n}$ est effectivement normal au plan P.
2. On cherche un vecteur normal $\vec{n_1}$ du plan P tel que la troisième coordonnée soit égale à 7.

On résout donc le système d’équations suivant :
$\begin{cases} 2a+4b = 0 \\ -a+b = 3 \\ 3a-3b+c = 7\end{cases}$
On trouve a=-2, b=1 et c=16, donc un vecteur normal $\vec{n_1}$ est $\vec{n_1} = (-2,1,16)$ .
3. On cherche un vecteur normal $\vec{n_2}$ du plan P tel que la deuxième coordonnée soit égale à -1. On résout donc le système d’équations suivant :
$\begin{cases} 2a+4b = 0 \\ -a+b = -1 \\ 3a-3b+c = 0\end{cases}$
On trouve a=1/2, b=3/2 et c=3, donc un vecteur normal $\vec{n_2}$ est $\vec{n_2} = (\frac{1}{2},-1,3)$ .
4. Pour qu’un vecteur normal ait sa première coordonnée égale à 4, il faudrait que le système d’équations suivant soit satisfait :
$\begin{cases} 2a+4b = 4 \\ -a+b = 0 \\ 3a-3b+c = 0\end{cases}$
En résolvant ce système, on trouve que la troisième équation implique que a=b, donc 2a+4b=6 .

Le système n’a donc pas de solution et il n’est pas possible de trouver un vecteur normal au plan P dont la première coordonnée est égale à 4.

Exercice 31 :
Le vecteur directeur de (d) est $\vec{u} = (-2,5,6)$ .

Un vecteur normal au plan P est donc colinéaire à $\vec{u}$ (car le plan est perpendiculaire à la droite) et à un vecteur reliant A à un point de (d) (car le plan passe par A).

Un point de (d) est par exemple B(1,6,-19), pour t=-4 :
$\begin{cases} x = 3-2t = 11 \\ y = 1+5t = 21 \\ z = -7+6t = -31 \end{cases}$
On a donc :
$\vec{AB} = \begin{pmatrix}11-8 \\ 21-(-5) \\ -31-3\end{pmatrix} = \begin{pmatrix}3 \\ 26 \\ -34\end{pmatrix},$
et un vecteur normal au plan P est donc $\vec{n} = \alpha\vec{u}\land\vec{AB}$

avec \alpha un réel quelconque. Par exemple, on peut prendre $\alpha=1$ pour simplifier les calculs :
$\vec{n} = \begin{pmatrix}-2 \\ 5 \\ 6\end{pmatrix}\land\begin{pmatrix}3 \\ 26 \\ -34\end{pmatrix} = \begin{pmatrix}-256 \\ -18 \\ -37\end{pmatrix}$
Une équation cartésienne de P est donc :

, ou encore .

Exercice 32 :

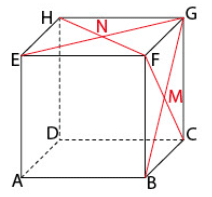
1. Les coordonnées de I et J sont respectivement :
$I = (\frac{1 }{2},0,0)$ (milieu de AB) et $J = (0,0,-\frac{1}{2})$ (milieu de DH).
Les coordonnées de G sont $(\frac{1}{2},\frac{1}{2},-\frac{1}{2})$ car G est le milieu de [EF] qui est parallèle à [AD].

2. Les points I, J et G sont sur les faces ABFE, DHCG et BCAD du cube respectivement, et ces faces sont toutes coplanaires.

On peut également remarquer que IJ est parallèle à BF et que IG est parallèle à BC, donc le plan IJG est parallèle à la face BCGF, qui est coplanaire avec les autres faces du cube.
3. a. Pour trouver un vecteur normal au plan IJG, on peut prendre le produit vectoriel des vecteurs $\vec{GI}$ et $\vec{GJ}$ :
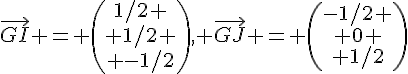
$\vec{GI} = \begin{pmatrix}1/2 \\ 1/2 \\ -1/2\end{pmatrix}, \vec{GJ} = \begin{pmatrix}-1/2 \\ 0 \\ 1/2\end{pmatrix}$ ,
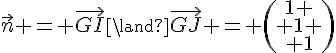
$\vec{n} = \vec{GI}\land\vec{GJ} = \begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}$ .
On peut vérifier que ce vecteur est bien normal au plan IJG en calculant le produit scalaire de $\vec{n}$ avec un vecteur appartenant au plan, par exemple $\vec{GI}$ ou $\vec{GJ}$ .
b. Une équation cartésienne du plan IJG est donc : avec d un réel quelconque.

Exercice 33 :
1. La droite (d1) a pour vecteur directeur $\vec{u_1} = (4,1,-1)$ et la direction normale au plan P est $\vec{n} = (2,-5,3)$ , donc pour savoir si (d1) est sécante avec P, il suffit de vérifier si $\vec{u_1}$ est orthogonal à $\vec{n}$ , c’est-à-dire si leur produit scalaire est nul :
$\vec{u_1}.\vec{n} = 4\times 2 + 1\times (-5) + (-1)\times 3 = 3$ , donc la droite (d1) n’est pas orthogonale au plan P et donc ils sont sécants.
2. On cherche l’intersection de la droite (d2) et du plan P, donc un point M commun aux deux. On a donc :
et x=2+3t, y=2t, z=1+5t.
On remplace x,y,z dans l’équation de P :
$2(2+3t)-5\times 2t +3(1+5t) = 7$ , soit 8t+8=0 , d’où t=-1.
L’intersection de (d2) et de P est donc le point M de coordonnées (5,-2,4).

Exercice 34 :
1. Pour vérifier que les points A, B et C ne sont pas alignés, on peut calculer le vecteur $\vec{AB}$ et le vecteur $\vec{AC}$ et vérifier qu’ils ne sont pas colinéaires :
$\vec{AB} = (1-0,3-4,0-1) = (1,-7,-1)$
$\vec{AC} = (2-0,-1-4,-2-1) = (2,-5,-3)$
Le déterminant de la matrice formée par ces deux vecteurs est non nul :
$\begin{vmatrix} 1 -7 -1 \\ 2 -5 -3 \end{vmatrix} = 14-2-35 = -23$ , donc $\vec{AB}$ et $\vec{AC}$ ne sont pas colinéaires et les points A, B et C ne sont pas alignés.
2. a. On doit vérifier que $\vec{u}$ est orthogonal à $\vec{n} = \vec{AB}\land\vec{AC}$ :
$\vec{u}.\vec{n} = 2\times (-7) + (-1)\times 2 + 3\times (-1) = -19$ , donc la droite $\Delta$ est bien orthogonale au plan ABC.
b. Un vecteur normal au plan ABC est $\vec{n} = \vec{AB}\land\vec{AC} = (-23,-5,1)$ .

Une équation cartésienne du plan ABC est donc .
c. Une représentation paramétrique de la droite $\Delta$ est :

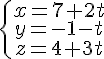
$\{\begin{matrix} x=7+2t \\ y=-1-t \\ z=4+3t \end{matrix}$ .
d. Le point H est l’intersection de la droite $\Delta$ et du plan ABC, donc H doit vérifier l’équation du plan et l’équation de la droite :
, soit .
En remplaçant d dans l’équation de la droite, on a les coordonnées de H :

3. a. P_1 a pour direction normale $\vec{n_1} = (1,1,1)$ et P_2 a pour direction normale $\vec{n_2} = (1,4,0)$ . Pour vérifier que P_1 et P_2 sont sécants, il suffit de vérifier que $\vec{n_1}$ et $\vec{n_2}$ ne sont pas colinéaires, c’est-à-dire de vérifier que leur produit vectoriel est non nul :
$\vec{n_1}\land\vec{n_2} = \begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}\land\begin{pmatrix}1 \\ 4 \\ 0\end{pmatrix} = \begin{pmatrix}-4 \\ 1 \\ 3\end{pmatrix}$ .
Ce vecteur est non nul, donc P_1 et P_2 sont sécants.
b. La droite (d) est l’intersection de P_1 et P_2 , donc elle est orthogonale à leurs directions normales $\vec{n_1}$ et $\vec{n_2}$ .

Un vecteur directeur de (d) peut donc être obtenu comme produit vectoriel de $\vec{n_1}$ et $\vec{n_2}$ :
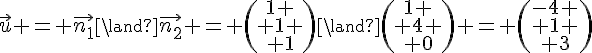
$\vec{u} = \vec{n_1}\land\vec{n_2} = \begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}\land\begin{pmatrix}1 \\ 4 \\ 0\end{pmatrix} = \begin{pmatrix}-4 \\ 1 \\ 3\end{pmatrix}$ .
La représentation paramétrique de (d) est donc :

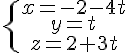
$\{\begin{matrix} x=-2-4t \\ y=t \\ z=2+3t \end{matrix}$ .
c. La droite (d) et le plan ABC ne sont ni sécants ni parallèles car le vecteur directeur de (d) n’est pas orthogonal au vecteur normal de ABC.

4.4/5 - (25322 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «produit scalaire : corrigé des exercices de maths en terminale en PDF.» au format PDF.

Ressources de terminale

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Produit scalaire : corrigé des exercices de maths en terminale en PDF.

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques