Continuité d’une fonction : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 18 septembre 2025
Exercice 1 :
soit f la fonction définie sur par
.
Indication : voici la courbe de cette fonction.
1. Etudier les variations de f sur .
2. Résoudre l’équation sur l’intervalle
.
On note cette solution .
Exercice 2 :
Montrer qu’une fonction continue sur R qui ne s’annule jamais est de signe constant.
Effectuons un raisonnement par l’absurde.
Considérons que cette fonction f continue sur R et qui ne s’annule jamais change de signe.
soit a<b alors imaginons le cas f(a)<0 et f(b)>0.
or comme f est continue sur R et que f(a)f(b)<0 d’après le théorème des valeurs intermédiaires
alors cela signifie qu’il existe tel que
cela signifierait que f s’annule or ce n’est pas le cas.
Conclusion : une fonction continue sur R qui ne s’annule jamais est de signe constant.
Exercice 3 :
Montrer que l’équation tan x = x possède une unique solution dans
Notons elle est définie et dérivable sur
donc f est strictement croissante et continue sur et change de signe sur
donc elle s’annule une seule fois sur
Exercice 4 :
Soit une application continue. On va montrer par récurrence que
admet un point fixe, c’est-à-dire qu’il existe
tel que
.
Pour , le théorème de la valeur intermédiaire assure que si
et
, alors
et
ou bien
et
(par exemple si
et
, alors l’image de
par
est contenue dans l’intervalle
qui ne contient pas
, ce qui contredit le fait que
). Par conséquent, il existe un
tel que
.
Supposons maintenant que le résultat est vrai pour tout entier inférieur ou égal à , et considérons une application continue
.
Si ou
, alors on a un point fixe et on a terminé.
Sinon, on peut appliquer le raisonnement précédent à la restriction de à l’intervalle
ou à l’intervalle
. Dans les deux cas, on obtient l’existence d’un point fixe
de cette restriction. Si
, alors on a terminé. Sinon, on a
ou
, donc on peut appliquer l’hypothèse de récurrence à la restriction de
à l’intervalle
ou à l’intervalle
. Dans les deux cas, on obtient l’existence d’un point fixe de cette restriction, qui est aussi un point fixe de
.
Exercice 5:
Soit f la fonction définie sur par
Montrer que f possède une unique racine puis en donner un encadrement d’amplitude 0, 01.
La fonctionf est dérivable sur
donc sur
donc f est strictement croissante sur .
et
f est strictement croissante et continue et passe d’une valeur négative à une valeur positive sur
donc
f possède une unique racine sur d’après le théorème de bijection.
Exercice 6 :
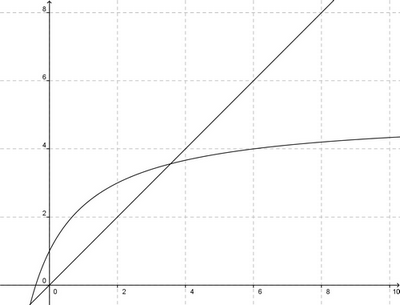
Soit P la fonction définie sur par
1. Dresser le tableau de variations de P.
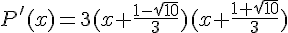
2. En déduire le nombre de racines de P.
P admet trois racines distinctes.
3. Retrouver directement ces racines en factorisant P(x)..
1 est une racine évidente
donc
Par identification des coefficients :
donc
ainsi
Conclusion : les trois racines distinctes sont .
Exercice 7 :
Montrer que tout polynôme de degré impair possède au moins une racine réelle.
Soit p un polynôme de degré impair
alors et
de plus P est un polynôme donc continue sur R.
P passe donc d’une valeur négative à une valeur positive donc d’après le théorème des valeurs intermédiaires,
il existe au moins une racine réelle.
Exercice 8 :
Soit f la fonction définie sur R par
Montrer que f possède une unique racine.
donc f est strictement croissante et continue sur R
de plus et
donc f passe d’une valeur égative à une valeur positive
on peut en déduire, d’après le théorème des valeurs intermédiaires, que f admet une unique racine sur R.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «continuité d’une fonction : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



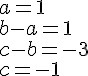
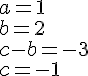
![f'(x)=5x^4+3x^2+1=5(x^4+\frac{3}{5}x^2+\frac{1}{5})\=5[(x^2+\frac{3}{10})^2-\frac{9}{100}+\frac{1}{5}] \=5[(x^2+\frac{3}{10})^2+\frac{11}{100}]>0](https://mathovore.fr/latex-images/b11865e324452cff3ada8d7bc8b620de.png)







