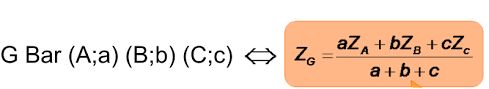Nombres complexes : cours de maths en terminale en PDF.
Mis à jour le 29 juin 2025
I. Notion de nombre complexe :
1. Théorème :
Il existe un ensemble noté 
, appelé ensemble des nombres complexes qui possède les propriétés suivantes :
- contient l’ensemble des nombres réels;
- L’addition et la multiplication des nombres réels se prolongent aux nombres complexes et les règles de calcul restent les mêmes.
- Il existe un nombre complexe noté i tel que ;
- Tout nombre complexe s’écrit de manière unique avec et réels.
Exemple :
z =3 + 5i ; z = – 3,7i ; z = – 7i sont des nombres complexes.
Un peu d’histoire :
En 1777, Euler introduit la lettre i, Gauss en généralisera l’emploi à partir de 1830.
2. Définition :
L’écriture z = x+iy avec x et y réels est appelée forme algébrique du nombre complexe z .
x est la partie réelle de z, notée Re(z).
y est la partie imaginaire de z, notée Im(z) .
Exemple :
z = -3 +5i alors Re(z) = -3 et Im(z) = 5
Remarque :
- Les parties réelles et imaginaires sont des nombres réels.
- Lorsque y=0, z est un réel et lorsque x=0, z= iy (y réel) est appelé imaginaire pur.
3. Propriété 1 :
Deux nombres complexes sont égaux si et seulement si, ils ont même partie réelle et même partie imaginaire.
Remarque :
- Cette propriété découle de l’unicité de l’écriture d’un nombre complexe sous forme algébrique.
- En particulier, x et y étant des réels, si et seulement si et .
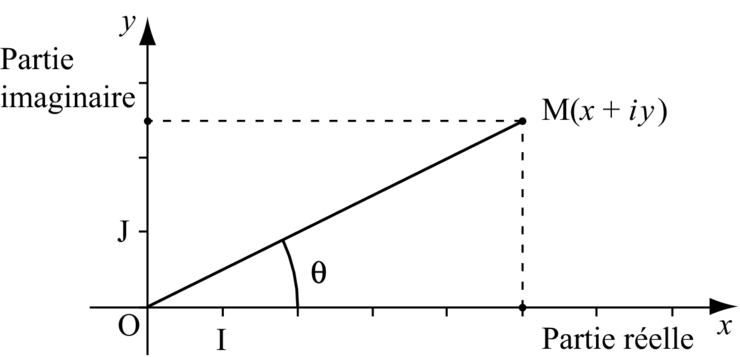
II. Représentation géométrique des nombres complexes.
Soit un repère orthonormé du plan .
1. Définition.
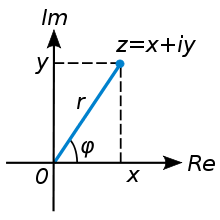
A tout nombre complexe avec et réels, on associe le point M de coordonnées .
On dit que
- M est le point image de z
- OM est le vecteur image de z.
- z est l’affixe du point M on note M(z)
Le plan est alors appelé plan complexe, noté P.
Remarque et vocabulaire :
- Les nombres réels sont les affixes des points de l’axe des abscisses appelé axe des réels .
- Les imaginaires purs sont les affixes des points de l’axe des ordonnées appelé aussi axe des imaginaires purs.
[2pi], on dit que est un repère direct .
III. Opérations sur les nombres complexes :
1. Addition et multiplication dans C :
1.1. Règles de calculs :
L’addition et la multiplication des nombres réels se prolonge aux nombres complexes et les règles de calcul restent les mêmes.
Exemple :
(car i² = – 1) .
Remarque :
- Les identités remarquables abordées en classe de 3° restent valables dans .
- Soit z et z’ éléments de C, équivaut à ou .
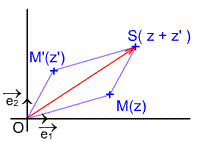
1.2. Représentations géométrique de la somme.
Deux nombres complexes et ont pour images respectives M et M’ dans le plan complexe .
a pour image le point S quatrième sommet du parallélogramme OMSM’ .
2. Inverse et quotient :
2.1. Propriété 2 :
Tout nombre complexe non nul z admet un inverse noté .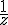
Pour obtenir la forme algébrique de :
((x,y) différent du couple (0;0)).
On multiplie numériquement le numérateur et le dénominateur par car est un nombre réel.
L’avantage est de faire disparaître le i au dénominateur.
Exemples :
Ecrire sous forme algébrique et .
3. Affixe d’un vecteur, d’un barycentre :
3.1. Propriété 3 :
Deux points A et B du plan complexe ont pour affixes respectives et .
L’affixe du vecteur est .
Remarques :
- Deux vecteurs sont égaux si et seulement si leurs affixes sont égales.
- Si k est un réel, l’affixe du vecteur est où z est l’affixe de .
3.2. Propriété 4 :
Deux points A et B du plan complexe ont pour affixes respectives et .
L’affixe du barycentre G des points pondérés et (avec non nul) est :
.
Remarque :
Ce résultat se généralise à plus de deux points.
Vous avez assimilé ce cours sur les nombres complexes en terminale ?
Effectuez ce QCM sur les nombres complexes en classe de terminale.
Un QCM sur les nombres complexes
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «nombres complexes : cours de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
