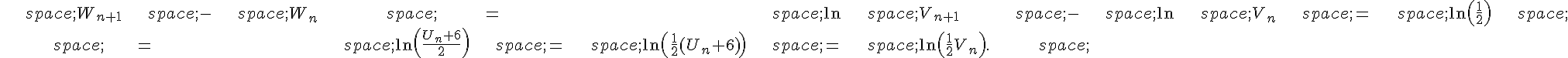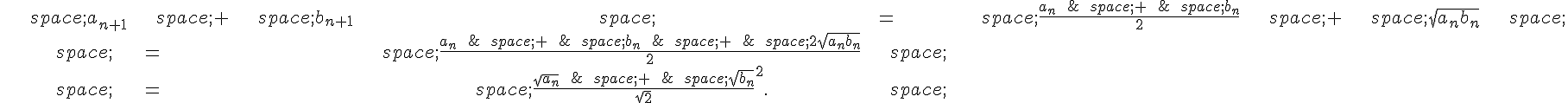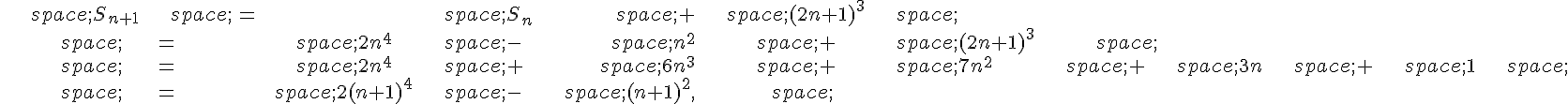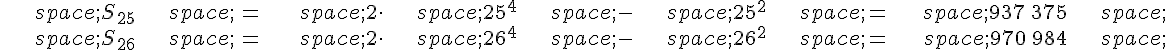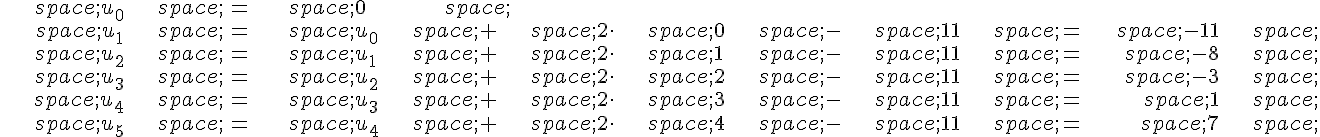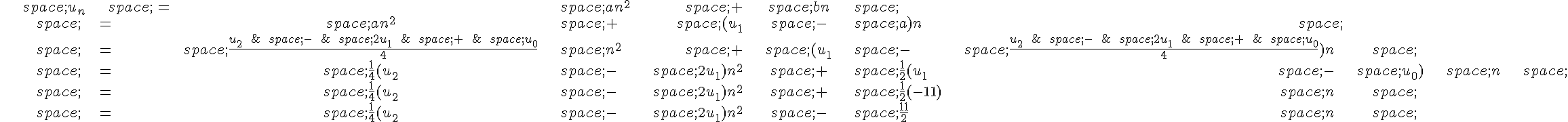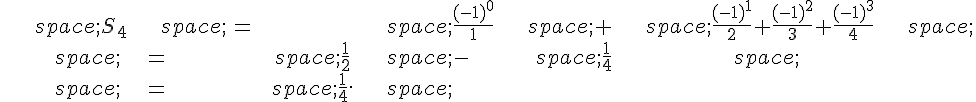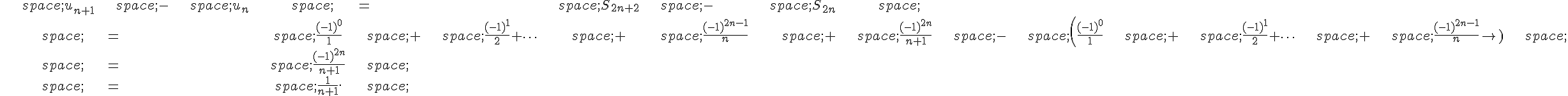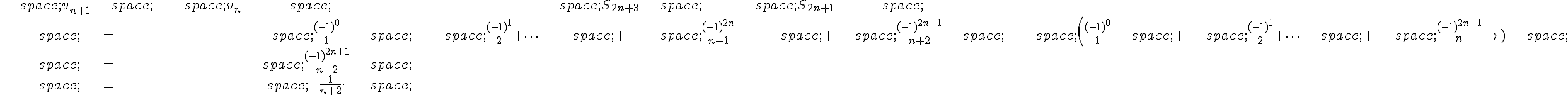Suite numériques : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 17 septembre 2025
Exercice 1 :
1. Soit la suite arithmétique de raison r=-2 et telle que
.
a. Calculer .
b. Calculer
Or .
2. Soit la suite géométrique de raison
et telle que
.
a. Calculer .
b. Calculer 
Or
Donc
Exercice 2 :
Calculer les limites des suites suivantes :
a.
b.
c.
d.
e. : sans limite
Exercice 3 :
Calculer les limites des suites suivantes :
a.
b.
Exercice 4 :
Calculer les limites des suites suivantes en utilisant le théorème des croissances comparées.
a.
b.
c.
Exercice 5 :
Etudier le sens de variation des suites suivantes :
a.
soit
donc est strictement croissante sur
b.
soit
La suite définie par est croissante et tend vers 0
donc il existe
A partir de , la suite étudiée est croissante.
c.
Pour
Nous pouvons donc calculer le rapport :
Pour
Donc la suite est décroissante sur
.
Exercice 6 :
Vérifions que la proposition est vraie au rang . On a
, donc c’est vrai.
Supposons maintenant que la proposition est vraie pour un certain entier , c’est-à-dire
. Montrons qu’elle est vraie aussi au rang
, c’est-à-dire
. On a :
Ainsi, on a prouvé par récurrence que .
Exercice 7 :
Vérifions que la proposition est vraie au rang . On a
et
, donc c’est vrai.
Supposons maintenant que la proposition est vraie pour un certain entier , c’est-à-dire
. Montrons qu’elle est vraie aussi au rang
, c’est-à-dire
. On a :
\[U_{n+1} = 2U_n – 3 = 2(3-2^n) – 3 = 6 – 2^{n+1} – 3 = 3 – 2^{n+1}.\]
Ainsi, on a prouvé par récurrence que .
Exercice 8 :
a. On a ,
,
et
.
b. On a :
Ainsi, on a la formule de récurrence .
c. On vérifie que . Supposons que
pour un certain entier naturel
. Alors :
ce qui prouve que la formule est vraie au rang .
D’après le principe de récurrence, cela prouve que la formule est vraie pour tout .
Exercice 9 :
Exercice 10 :
1.a. On a , donc
Ainsi, la suite est une suite géométrique de raison
et de terme initial
.
1.b. On a :
En utilisant que , on a
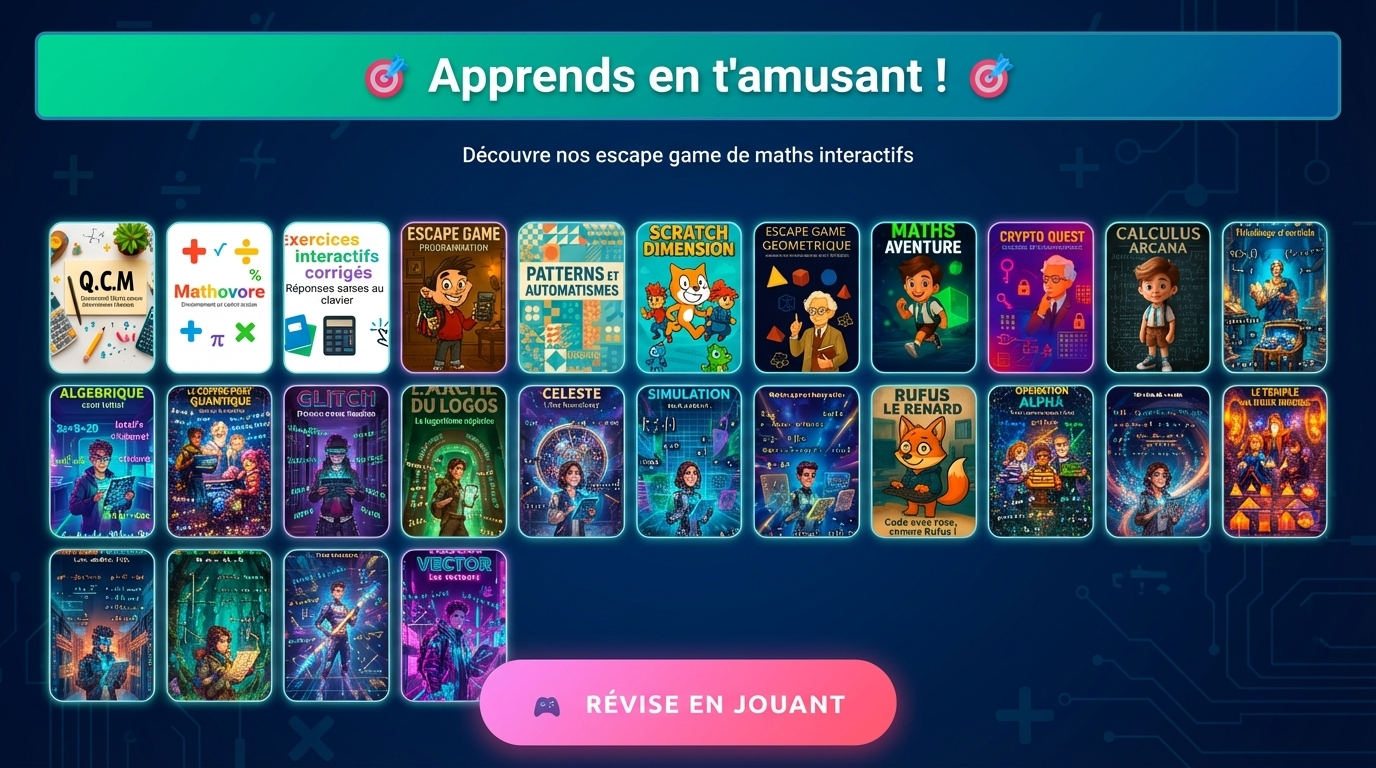
1.c. Comme , on a
. Ainsi, d’après la formule pour la somme d’une suite géométrique, on a :
De même, car
.
2. On a . On calcule :
Ainsi, la suite est une suite arithmétique de raison
.
On a :
On a , donc
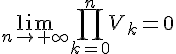
Ainsi, on a :
3. On a .
En utilisant que pour tout
, on a :
Exercice 11 :
1. Soit une suite convergente de limite
.
Par définition, cela signifie que pour tout , il existe un entier naturel
tel que pour tout
,
.
En particulier, pour , il existe un entier naturel
tel que pour tout
,
Cela signifie que
dès que
.
Donc la suite est bornée.
2. Soit une suite croissante et non majorée.
On montre que diverge vers
. En effet, pour tout
, comme
n’est pas majorée, il existe un indice
tel que
.
De plus, comme est croissante, pour tout
, on a
.
Donc la suite est
-supérieure à partir d’un certain rang indépendant de
, ce qui signifie que
tend vers
.
3. Supposons qu’une suite converge vers deux limites distinctes
et
.
Alors, pour tout , il existe
tel que pour tout
, on ait
et il existe
tel que pour tout
, on ait
. Soit
.
Alors, pour tout , on a à la fois :
et
En ajoutant ces deux inégalités, on obtient :
Mais ce n’est possible que si , ce qui contredit notre hypothèse de départ. Ainsi, la limite d’une suite est unique.
4. La suite n’a pas de limite.
En effet, si elle avait une limite , alors pour tout
, il existerait un entier
tel que pour tout
, on aurait
.
Mais la suite n’est pas convergente par oscillation : si
est pair,
et pour
impair,
.
Ainsi, pour tout , on peut trouver
et
pairs tels que
et
et
et
, et donc
(
) ce qui contredit la convergence de
.
5. Soit une suite bornée et
une suite convergeant vers
.
Il existe donc une constante telle que
pour tout
. Par ailleurs, puisque
converge vers
, pour tout
, il existe un entier
tel que pour tout
, on ait
.
En combinant ces deux inégalités, on en déduit que :
pour . Cela signifie que
converge également vers
.
6. Soit une suite d’entiers relatifs convergeant vers un réel
.
Soit . Puisque
converge vers
, il existe un entier
tel que pour tout
, on ait
. Mais ceci implique que pour tout
:
puisque .
Donc, à partir de l’indice , tous les termes de la suite sont à une distance strictement inférieure à

est stationnaire à partir de l’indice
et donc converge vers l’entier relatif
égal à cette valeur commune.
7. Soit une suite divergente vers
.
Pour tout , on a
, donc la suite est minorée par
. En effet, si elle ne l’était pas, il existerait un entier
tel que
, ce qui serait en contradiction avec l’hypothèse de divergence. Ainsi, la suite
est minorée par
.
Exercice 12 :
1. Pour tout entier , on a :
Or, puisque , on a
pour tout
.
Ainsi, on en déduit que pour tout
.
Donc est une suite croissante majorée par
, et donc elle converge vers une limite
. Par ailleurs, la suite
est décroissante, minorée par
et converge donc vers une limite
. De même, la suite
est décroissante, minorée par
, et converge donc vers une limite
. Nous allons montrer que
.
Pour tout entier , on a :
Ainsi, est une suite bornée et converge vers une limite
. Mais on a aussi, pour tout
,
Donc, en passant à la limite quand , on a
. Cela montre que
, donc on a
, donc
.
Ainsi, les deux suites convergent vers la même limite.
2. La suite ne converge pas car elle prend des valeurs aussi proches que l’on veut de
et en alternance. Plus précisément, pour tout
, on a
. La suite
ne converge pas non plus, car sinon on aurait par la formule trigonométrique
, ce qui est impossible sous l’hypothèse de convergence infinie de
.
Exercice 13 :
1. Nous allons procéder par récurrence sur .
Pour , on a
.
Supposons maintenant que l’inégalité est vraie pour un certain entier naturel , c’est-à-dire
. En multipliant par
des deux côtés de l’inégalité, on obtient
.
Puisque est positif, on a
, donc
, ce qui achève la démonstration par récurrence.
2. Si , alors
est une suite strictement croissante de réels positifs, donc elle diverge vers
. Si
, alors
est constante et converge vers 1. Si
, alors
(puisque
) et donc
lorsque
.
Enfin, si , alors
n’a pas de limite car lorsque
est pair,
est positif et lorsque
est impair,
est négatif. Donc la suite
ne peut pas converger vers une limite.
Exercice 14 :
1. Nous allons procéder par récurrence forte. Pour , on a
, donc la propriété est vraie pour
. Supposons maintenant que la propriété est vraie pour
, c’est-à-dire
Nous allons montrer que la propriété est alors vraie pour . Pour cela, on a
ce qui montre la propriété pour .
Par récurrence forte, la propriété est donc vraie pour tout .
2. On cherche donc le plus petit entier tel que
. On sait que
Il suffit donc de chercher le plus petit entier tel que
. On remarque que
, donc
.
On calcule ensuite les valeurs de et
:
On voit donc que est bien entre ces deux valeurs, donc la solution cherchée est
.
Exercice 15 :
Soient une suite croissante et majorée
et une suite décroissante et minorée.
Les suites et
ont-elles nécessairement la même limite ?
Il y a aucune raison pour qu’elles aient la même limite.
Si elles avaient la même limite ce serait des suites adjacentes .
la suite est décroissante et minorée par 3 .
la suite et croissante et majorée par 0 .
or et
.
Exercice 16 :
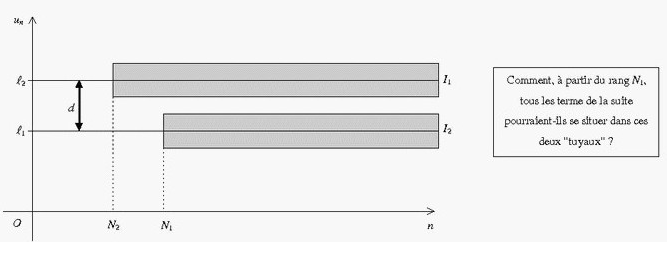
Indication : utiliser le théorème de comparaison.
On suppose connu le résultat suivant :
La suite tend vers
lorsque n tend vers
si tout
intervalle de la forme contient toutes les valeurs de
à partir d’un certain rang.
Soient et
deux suites telles que :
* est inférieur ou égal à
à partir d’un certain rang ;
* tend vers
lorsque n tend vers
.
Démontrer que la suite tend vers
lorsque n tend vers
.
Exercice 17 :
Soit telle que
et pour tout entier naturel n,
.
Soit telle que , pour tout entier naturel n,
.
1. Démontrer que la suite est arithmétique de raison
.
Indication : calculer et montrer que cette différence ne dépend pas de n.
2. Exprimer en fonction de n et en déduire que pour tout entier naturel n,
.
3. Calculer la limite de la suite et celle de la suite
.
Exercice 18 :
Soit la suite définie par son premier terme
et pour tout entier naturel n, .
1. Démontrer par récurrence que pour tout entier naturel n,
2. Etudier le sens de variation de la suite
3. Etudier la convergence de la suite
Exercice 19 :
1. On calcule les six premiers termes de la suite :
2. La courbe semble être une parabole.
On peut conjecturer que la fonction représentée par cette courbe est une fonction quadratique de la forme .
Par ailleurs, on pourrait conjecturer que la suite a pour terme général
, où
,
et
sont des constantes à déterminer.
3. Pour démontrer cette conjecture, on va utiliser la méthode des différences finies. On calcule d’abord la première différence :
On calcule ensuite la deuxième différence :
On remarque que la deuxième différence est constante et égale à .
Cela nous indique que la fonction représentée par la courbe est bien une fonction quadratique. On peut donc écrire .
Par ailleurs, on sait que , donc
. On a également
, donc
. Enfin, on sait que
, donc
.
On peut maintenant exprimer le terme général de la suite :
On a donc bien vérifié la conjecture annoncée à la question précédente.
Exercice 20 :
1. On calcule les six premiers termes de la suite :
2. La courbe semble être une parabole. On peut conjecturer que la fonction représentée par cette courbe est une fonction quadratique de la forme .
Par ailleurs, on pourrait conjecturer que la suite a pour terme général
, où
,
et
sont des constantes à déterminer.
3. Pour démontrer cette conjecture, on va utiliser la méthode des différences finies. On calcule d’abord la première différence :
On calcule ensuite la deuxième différence :
On remarque que la deuxième différence est constante et égale à .
Cela nous indique que la fonction représentée par la courbe est bien une fonction quadratique. On peut donc écrire .
Par ailleurs, on sait que , donc
. On a également
, donc
. Enfin, on sait que
, donc
.
On peut maintenant exprimer le terme général de la suite :
On a donc bien vérifié la conjecture annoncée à la question précédente.
Exercice 21 :
Nous allons prouver par récurrence que pour tout entier
.
Pour et
, on a respectivement
et
, donc la propriété est vraie pour
et
.
Supposons maintenant que la propriété est vraie pour et
, c’est-à-dire que
et
.
On va montrer que la propriété est alors vraie pour , c’est-à-dire que
.
En utilisant la relation de récurrence, on a
ce qui montre la propriété pour .
Par récurrence, la propriété est donc vraie pour tout entier , c’est-à-dire que pour tout entier
, on a
.
Exercice 22 :
1. On calcule les quatre premiers termes de la suite :
2. D’après leur définition, on a et
.
On veut montrer que est croissante,
est décroissante et que
tend vers
quand
tend vers l’infini.
Pour montrer que est croissante, on considère
, on a
Ainsi, est une suite croissante.
De même, pour montrer que est décroissante, on considère
, on a
Ainsi, est une suite décroissante.
Enfin, pour montrer que tend vers
quand
tend vers l’infini, on a
et donc
La suite tend donc vers
quand
tend vers l’infini, ce qui montre que
et
sont adjacentes.
En conclusion, les suites et
sont adjacentes et convergent vers une même limite, qui est
.
Exercice 23 :
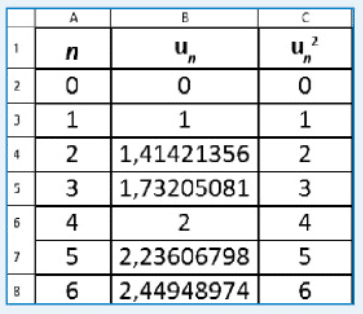
En observant les premières valeurs de et
, on peut conjecturer que
pour tout
.
On peut le démontrer par récurrence.
Initialisation :
Pour n=0, on a . L’hypothèse est vérifiée au rang 0.
Hérédité :
Supposons que vraie pour un certain entier n.
Alors,
.
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :
On en déduit que pour tout
.
Exercice 24 :
Initialisation :
Pour n=0, on a . L’hypothèse est vérifiée au rang 0.
Hérédité :
Supposons que soit vraie pour un certain entier n.
Alors,
.
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :
On en déduit que pour tout .
Exercice 25 :
Initialisation :
Pour n=0, on a .
L’hypothèse est vérifiée au rang 0.
Hérédité :
Supposons pour un certain entier n.
On a alors :
.
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :
On en déduit que pour tout entier naturel n.
Exercice 26 :
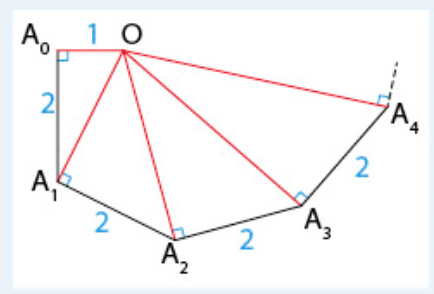
Initialisation :
Pour n=0, on a .
L’hypothèse est vérifiée au rang 0.
Hérédité :
Supposons que pour un certain entier n.
On a alors :
.
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :
On en déduit que pour tout
.
Exercice 27 :
1) a) On a et donc
.
b) On a et donc
.
c) On a et
, donc
.
d) On peut réécrire sous la forme \frac{4^n}{3^n}+\frac{5}{3^n}. On a
et
, donc
.
2) a) Le premier terme de la suite est -3.
On peut écrire .
En effet,
.
b) La suite est convergente car
, et sa limite est
.
Exercice 28 :
On a .
Ainsi, .
On en déduit que la limite de la suite est
.
Exercice 29 :
1) a) La fonction f est dérivable sur et on a
pour tout
.
Donc, f est strictement croissante sur .
b) Si , alors
.
2) Initialisation :
Pour n=0, on a .
L’hypothèse est vérifiée au rang 0.
Hérédité :
Supposons que pour un certain entier n soit vraie.
Alors, et
, donc
et
.
Ainsi, l’hypothèse est vérifiée au rang.
Conclusion :
On en déduit que pour tout .
3) La suite est décroissante et minorée par 0, donc elle converge.
Soit l sa limite.
En passant à la limite dans la relation de récurrence, on a .
Cette équation admet comme solution, qui est la seule solution possible car f est strictement croissante sur [0;1].
Ainsi, la suite converge vers 0.
Exercice 30 :
1) Les dix premiers termes de la suite sont :
1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
2) a) On peut conjecturer que u_n=n^2.
b) Initialisation :
Pour n=1, on a . L’hypothèse est vérifiée au rang 1.
Hérédité :
Supposons que pour un certain entier n.
Alors,
.
Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :
On en déduit que pour tout .
Exercice 31 :
Initialisation :
Pour n=1, on a .
L’hypothèse est vérifiée au rang 1.
Hérédité :
Supposons 
Alors,
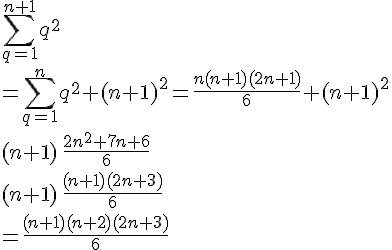
Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :
On en déduit que pour tout entier naturel n non nul,
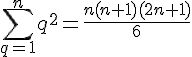
Exercice 32 :
1) a) On a car
qui tend vers 0 quand n tend vers l’infini.
b) On a .
c) On a 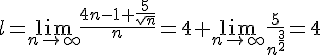
d) On a .
2) a) La suite est géométrique de raison 0,8 et de premier terme -3.
Ainsi, .
b) On a .
3) Les trois dernières suites tendent toutes vers 0, donc elles sont bornées.
Exercice 33 :
1) On a .
Ainsi, la suite est géométrique de raison
, et son premier terme est
.
2) On peut écrire .
Ainsi, .
3) La suite tend vers
.
Exercice 34 :
1) On a .
Comme , on a
lorsque
.
Donc lorsque
.
Par conséquent, la suite est bornée.
2) On a pour tout entier naturel $n$.
Donc .
Ainsi, est bornée.
3) La fonction est continue et décroissante sur
.
On a pour tout entier naturel
, donc
pour tout entier naturel $n$.
Ainsi, est bornée.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «suite numériques : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



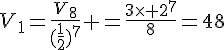
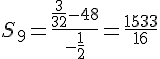
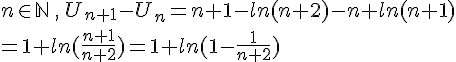
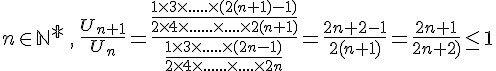
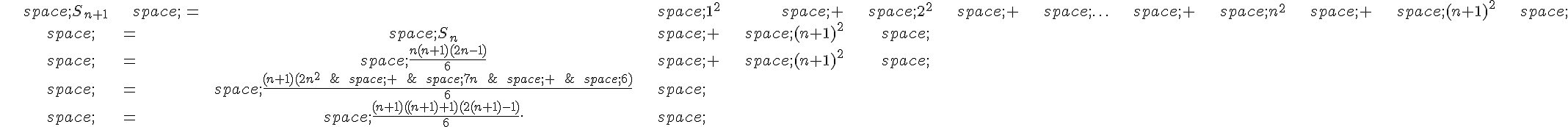
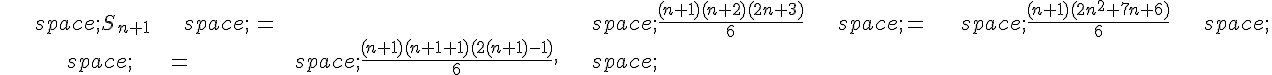
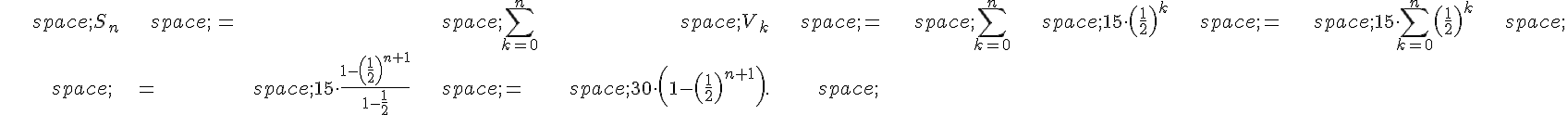
![\[S_n'\,=\,\sum_{k=0}^n\,U_k\,=\,\sum_{k=0}^n\,(V_k\,-\,6)\,=\,S_n\,-\,6(n+1).\]](https://mathovore.fr/latex-images/b18331f091d07718bebb189404ea403b.png)