Bac maths 2024 aux centres étrangers : sujet et corrigé

Bac de maths 2024 aux centres étrangers avec le sujet n° 1 et son corrigé. Ce sujet porte sur une fonction rationnelle et son sens de variation. Des probabilités sur la lutte contre le dopage. Une fonction exponentielle à étudier avec une suite récurrente et un programme réalisé avec Python. Une équation différentielle et une intégrale à calculer. Des équations paramétriques et cartésiennes dans l’espace.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
Centres Etrangers – SESSION 2024
MATHÉMATIQUES
Jour 1
Durée de l’épreuve : 4 heures

L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire « type collège » est autorisé.

La qualité de la rédaction, la clarté et la précision des raisonnements seront prises en
compte dans l’appréciation de la copie. Les traces de recherche, même incomplètes
ou infructueuses, seront valorisées.

Exercice 1 (5 points)
Partie A
On définit la fonction sur l’intervalle [0 ; 1] par :
$f(x)\,=\frac{0,96x}{0,93x\,+\,0,03}$

1. Démontrer que, pour tout appartenant à l’intervalle [0 ; 1],

$f'(x)\,=\frac{0,0288}{(0,93x\,+\,0,03)^2}$

2. Déterminer le sens de variation de la fonction sur l’intervalle [0 ; 1].

Partie B
La lutte contre le dopage passe notamment par la réalisation de contrôles antidopage
qui visent à déterminer si un sportif a fait usage de substances interdites.
Lors d’une compétition rassemblant 1000 sportifs, une équipe médicale teste tous les
concurrents. On propose d’étudier la fiabilité de ce test.

On appelle le réel compris entre 0 et 1 qui désigne la proportion de sportifs dopés.

Lors de l’élaboration de ce test, on a pu déterminer que :

la probabilité qu’un sportif soit déclaré positif sachant qu’il est dopé est égale
à 0,96 ;
la probabilité qu’un sportif soit déclaré positif sachant qu’il n’est pas dopé est
égale à 0,03.

On note :

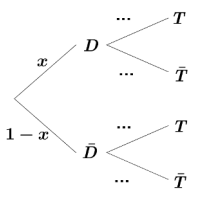
D l’événement : « le sportif est dopé ».
T l’événement : « le test est positif ».

1. Recopier et compléter l’arbre de probabilité ci-dessous :

2. Déterminer, en fonction de , la probabilité qu’un sportif soit dopé et ait un test
positif.
3. Démontrer que la probabilité de l’événement est égale à $0,93x\,+\,0,03$ .
4. Pour cette question uniquement, on suppose qu’il y a 50 sportifs dopés parmi les
1000 testés.
La fonction désigne la fonction définie à la partie A.
Démontrer que la probabilité qu’un sportif soit dopé sachant que son test est positif est
égale à .

En donner une valeur arrondie au centième.
5. On appelle valeur prédictive positive d’un test la probabilité que le sportif soit
réellement dopé lorsque le résultat du test est positif.

a. Déterminer à partir de quelle valeur de la valeur prédictive positive du test étudié
sera supérieure ou égale à 0,9. Arrondir le résultat au centième.

b. Un responsable de la compétition décide de ne plus tester l’ensemble des
sportifs, mais de cibler les sportifs les plus performants supposés être plus
fréquemment dopés.
Quelle est la conséquence de cette décision sur la valeur prédictive positive du
test ? Argumenter en utilisant un résultat de la partie A.

Exercice 2 (5 points)
On considère la fonction définie sur l’intervalle [0; 1] par $f(x)=2xe^{-x}$ .
On admet que la fonction est dérivable sur l’intervalle [0; 1].

1. a. Résoudre sur l’intervalle [0; 1] l’équation .
b. Démontrer que, pour tout appartenant à l’intervalle [0; 1], $f'(x)\,=\,2(1\,-\,x)e^{-x}$ .
c. Donner le tableau de variations de la fonction sur l’intervalle [0 ; 1].
On considère la suite définie par $u_0=\,0,1$ et pour tout entier naturel , $u_{n+1\,}=\,f(u_n)$ .
2. a. Démontrer par récurrence que, pour tout entier naturel, $0\,\leq\,\,u_n\,<\,u_{n+1}\,\leq\,\,1.$
b. En déduire que la suite est convergente.
3. Démontrer que la limite de la suite est .
4. a. Justifier que pour tout entier naturel , $ln(2)\,-\,u_n$ est positif.
b. On souhaite écrire un script Python qui renvoie une valeur approchée de ln(2)
par défaut à $10^{^-4}$ près, ainsi que le nombre d’étapes pour y parvenir.
Recopier et compléter le script ci-dessous afin qu’il réponde au problème posé.

c. Donner la valeur de la variable n renvoyée par la fonction seuil().

Exercice 3 (5 points)
On considère l’équation différentielle $(E_0)\,:\,y'\,=\,y$ où est une fonction dérivable
de la variable réelle .
1. Démontrer que l’unique fonction constante solution de l’équation différentielle
est la fonction nulle.
2. Déterminer toutes les solutions de l’équation différentielle .

On considère l’équation différentielle $(E)\,:\,y'\,=\,y-\,cos(x)\,-\,3sin(x)$ où est une
fonction dérivable de la variable réelle .

3. La fonction est définie sur $\mathbb{R}$ par $h(x)\,=\,2\,cos(x)\,+\,sin\,(x)$ .
On admet qu’elle est dérivable sur $\mathbb{R}$ .
Démontrer que la fonction est solution de l’équation différentielle .

4. On considère une fonction définie et dérivable sur $\mathbb{R}$ .
Démontrer que : « est solution de » est équivalent à « est solution de ».
5. En déduire toutes les solutions de l’équation différentielle .
6. Déterminer l’unique solution de l’équation différentielle telle que $g(0)\,=\,0$ .

7. Calculer :

$\int_{0}^{\frac{\pi}{2}}(-2e^x+sin(x)+2cos(x))dx$ .

Exercice 4 (5 points)
L’espace est muni d’un repère orthonormé $(O,\vec{i},\vec{j},\vec{k})$ .
On considère :
les points (−2; 0; 2), (−1 ; 3; 0), (1 ; −1; 2) et (0; 0; 3).

la droite dont une représentation paramétrique est :

$\{\begin{matrix}\,x\,=\,t\,\\\,y\,=\,3t\,\\\,z\,=\,3\,+\,5t\,\end{matrix}.$ avec $t\in\,\mathbb{R}$ .

la droite dont une représentation paramétrique est :

$\{\begin{matrix}\,x\,=\,1+3s\,\\\,y\,=\,-1-5s\,\\\,z\,=\,2-6s\end{matrix}.$ avec $s\in\,\mathbb{R}$ .

1. Démontrer que les points et ne sont pas alignés.

2. a. Démontrer que le vecteur $\vec{n}\begin{pmatrix}\,1\,\\\,3\,\\\,5\,\end{pmatrix}$ est orthogonal au plan .
b. Justifier qu’une équation cartésienne du plan est :

$x\,+\,3y+\,5z\,-\,8\,=\,0$

c. En déduire que les points $A,\,B,\,C$ et ne sont pas coplanaires.
3. a. Justifier que la droite est la hauteur du tétraèdre issue de .
On admet que la droite est la hauteur du tétraèdre issue de .
b. Démontrer que les droites et sont sécantes et déterminer les coordonnées
de leur point d’intersection.
4. a. Déterminer les coordonnées du projeté orthogonal du point sur le plan .
b. Calculer la distance du point au plan . Arrondir le résultat au centième.

Consulter le corrigé

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac maths 2024 aux centres étrangers : sujet n° 1 corrigé» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.