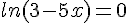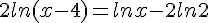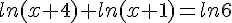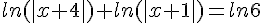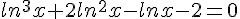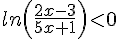Logarithmes : exercices de maths en terminale corrigés en PDF.
Mis à jour le 21 décembre 2025
Exercice 1
• Exprimer en fonction de ln 2 et ln 3 :
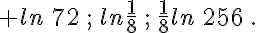
• Exprimer en fonction de ln 2 et ln 5 :
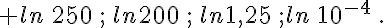
Exercice 2
Simplifier les expressions suivantes :
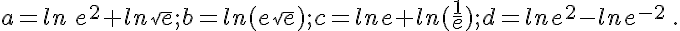
Exercice 3
Soit n un entier naturel non nul et a un nombre réel strictement positif.
Calculer la somme :
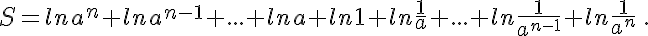
Exercice 4
Etudier les limites suivantes :
a. 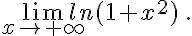
b. 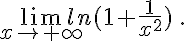
c. 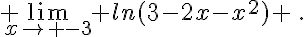
d. 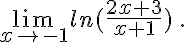
d. 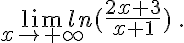
e. 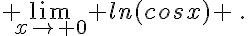
f. 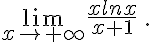
Exercice 5 : recherche d’asymptotes.
Indiquer l’ensemble de définition de la fonction f, puis étudier les limites aux bornes de cet ensemble.
Préciser les asymptotes à la courbe représentant f.
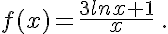
Exercice 6
Résoudre dans 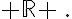 chacune des équations suivantes :
chacune des équations suivantes :
a. 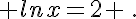
b. 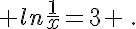
c. 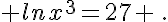
d. 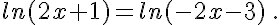
e. 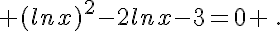
Exercice 7
Résoudre le système suivant :
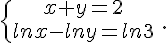
Exercice 8
Déterminer la fonction dérivée de la fonction f sur l’ensemble 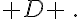
a. ![f(x)=ln(-x)\,\,D=]-\infty\,;\,0[ \,.](https://mathovore.fr/latex-images/a331965b1abcb8feda9853fb981549d8.png)
b. ![f(x)=ln(\sqrt{x})\,\,D=]0\,;\,+\infty\,[ \,.](https://mathovore.fr/latex-images/fb25fea67cdcb7c69be1b3baab30319a.png)
c. ![f(x)=ln(\frac{x+1}{x-1})\,\,D=]-\infty\,;\,-1[ \,.](https://mathovore.fr/latex-images/5ab0fe83a479ee5644c1112ea241126c.png)
Exercice 9 – Equation du troisième degré dans le corps des complexes
On considère dans l’ensemble des complexes le polynôme :
P(z) = z³ + (2i-5)z² +7(1-i)z -2 +6i
1- Sachant que a étant un réel, on a P(a) = 0. Déterminez a.
2- Trouvez toutes les solutions de P(z) =0. En déduire une factorisation de P(z).
Exercice 10 – Inéquations
Résoudre les inéquations suivantes :
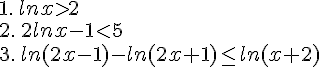
Exercice 11 – Equations et logarithmes népériens
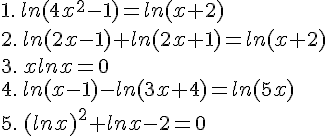
Exercice 12 – Résoudre des équations logarithmiques
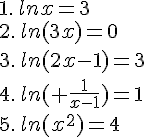
Exercice 13 – Simplifier des logarithmes népériens
Simplifier :
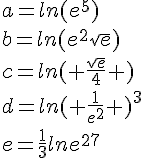
Exercice 14 – Exprimer en fonction de ln 2 et ln 3
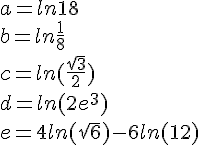
Exercice 15 -Logarithme népérien (ln)
Résoudre les équations et inéquations suivantes :
Exercice 16 -Prise d’initiative et nombres complexes
Lequel de ces deux nombres est le plus grand ?
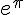 ou
ou 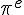 .
.
Indication :
On peut faire une conjecture à la calculatrice mais on donnera une vraie démonstration.
Exercice 17 -Signe d’une fonction
soit g définie sur ]0;+infini[ par g(x)= 2x²+1-ln(x)
quel est le signe de g pour x>0?.
Exercice 18 -Dérivée
Soit g la fonction définie sur ]0;+ [ par: g(x) = 1-x2– ln(x)
[ par: g(x) = 1-x2– ln(x)
1.calculer la dérivée de la fonction g et étudier son signe. En déduire les variations de la fonction g
2. Calculer g(1). En déduire le signe de g(x) pour x appartenant à l’intervalle ]0;+ [ .
[ .
Exercice 19 -Logarithme népérien et simplifications
1) simplifier 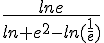
2) Déterminer le plus petit entier n tel que 1,05n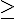 1,5
1,5
3) Chaque année, la population d’une ville diminue de 3%. Au bout de combien d’année, la population de cette ville aura-t-elle diminué de plus de 30%.
Exercice 20 – Bac et logarithmes
Partie A :
Soit g la fonction définie pour tout nombre réel x de l’intervalle ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par  .
.
1.Déterminer les limites de la fonction g en 0 et  .
.
2.Montrer que g est dérivable sur l’intervalle ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et que
et que 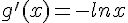 .
.
3.Dresser le tableau de variations de la fonction g.
Partie B :
soit 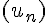 la suite définie pour tout
la suite définie pour tout 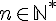 par
par 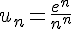 .
.
1.Conjecturer, à l’aide de la calculatrice ;
a. le sens de variation de la suite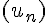 ;
;
b. la limite éventuelle de la suite 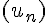 .
.
2.Soit 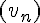 la suite définie pour tout
la suite définie pour tout 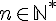 par
par 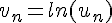 .
.
a. Montrer que 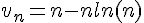 .
.
b. En utilisant la partie A, déterminer le sens de variation de la suite 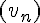 .
.
3.Montrer que la suite 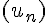 est bornée.
est bornée.
4.Montrer que la suite 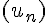 est convergente et déterminer sa limite.
est convergente et déterminer sa limite.
Exercice 21 – comparaison entre 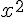 et
et 
Soit f la fonction définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par 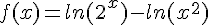 .
.
1. Démontrer que 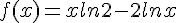 .
.
2. Calculer f(2) et f(4).
3. Calculer la dérivée f ‘ de f.
En déduire les variations de f.
4. A l’aide des questions 2 et 3, préciser le signe de f.
5. Déterminer l’ensemble des entiers n pour lesquels on a 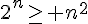 .
.
Exercice 22 :
Résoudre les équations suivantes :
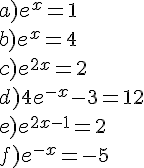
Exercice 23 :
Résoudre les équations suivantes :
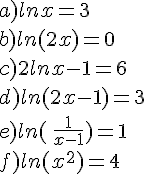
Exercice 24 :
Simplifier l’écriture des nombres suivants :
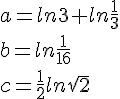
Exercice 25 :
Après avoir préciser l’ensemble de définition des solutions de l’équation, la résoudre.
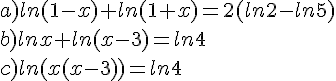
Exercice 26 :
Soit la fonction f définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par :
par : 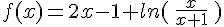 .
.
On note  sa représentation graphique dans un repère orthonormé
sa représentation graphique dans un repère orthonormé 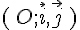 du plan (unité graphique : 2 cm).
du plan (unité graphique : 2 cm).
1. Étudier la limite de f en 0. Interpréter graphiquement ce résultat.
2. a. Étudier la limite de f en  .
.
b. Démontrer que la droite 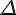 d’équation
d’équation 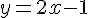 est une asymptote à
est une asymptote à  en
en  .
.
Étudier la position de  par rapport à
par rapport à 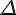 .
.
3. Étudier les variations de f. Dresser son tableau de variations.
4. Démontrer que l’équation f(x) = 0 admet une unique solution  dans l’intervalle
dans l’intervalle ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) et déterminer un encadrement de
et déterminer un encadrement de  d’amplitude
d’amplitude 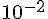 .
.
5. Tracer la droite 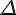 et la courbe
et la courbe  .
.
Exercice 27 :
Utile aussi pour le bac… en Chimie !
On sait, en Chimie, que le pH d’une solution permet d’exprimer son caractère acide ou basique.
Ce nombre est un décimal compris entre 1 et 14 de sorte que :
● Si pH < 7, alors la solution est dite acide.
● Si pH > 7, alors la solution est dite basique.
● Si pH = 7, elle est dite neutre.
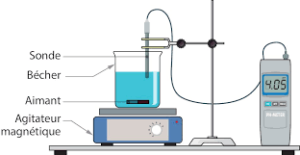
On sait alors que le pH est associé à la relation ![pH\,=\,-\,log[H_3O^{+}]](https://mathovore.fr/latex-images/285fdae8d605d4bc2daa1b0855bae6b7.png) où
où ![[H_3O^+]](https://mathovore.fr/latex-images/3f04897ab017b0f86a076f1e6e3ac68d.png) est la concentration en ions
est la concentration en ions 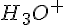 , exprimée en mol/L.
, exprimée en mol/L.
1. Une solution possède une concentration en ions 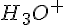 égale à
égale à 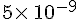 .
.
Quel est son pH ? Que peut-on dire d’une solution dont la concentration en ions 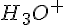 est
est
égale à 0,1 ?
2. Quelle est la concentration en ions 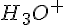 d’une solution neutre ?
d’une solution neutre ?
3. Si l’on augmente la concentration en ions 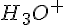 dans une solution, diminue-t-on ou augmente-t-on le pH de cette solution ?
dans une solution, diminue-t-on ou augmente-t-on le pH de cette solution ?
4. Que faut-il faire à une solution pour incrémenter ou décrémenter son pH ?
Vocabulaire : Incrémenter, c’est ajouter 1. Donc décrémenter, c’est… ?
Exercice 28 :
f est la fonction définie sur  par :
par :
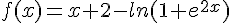 .
.
C est sa courbe dans un repère orthogonal 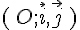 .
.
1. a. Déterminer la limite de 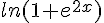 en
en 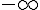 .
.
b. En déduire l’existence d’une asymptote oblique 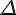 dont on précisera une équation.
dont on précisera une équation.
c. Montrer que pour tout réel x :
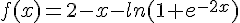
d. Déterminer la limite de f en  , ainsi que l’existence d’une seconde asymptote oblique
, ainsi que l’existence d’une seconde asymptote oblique
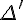 .
.
2. Montrer que l’axe des ordonnées est un axe de symétrie pour C.
3. Résoudre l’inéquation 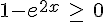 .
.
4. Étudier les variations de la fonction f.
5. Représenter 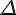 ,
, 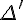 et C, après avoir indiqué la position de
et C, après avoir indiqué la position de  et C.
et C.
Exercice 29 :
La température 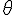 (en °C) d’un liquide peut être modélisée en fonction du temps t, en min, par :
(en °C) d’un liquide peut être modélisée en fonction du temps t, en min, par :
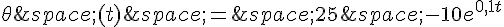
Donner les réponses arrondies au dixième.
a) Au bout de combien de temps la température atteindra-t-elle 12,5 °C ?
b) Au bout de combien de temps la température atteindra-t-elle 0°C ?
Exercice 30 :
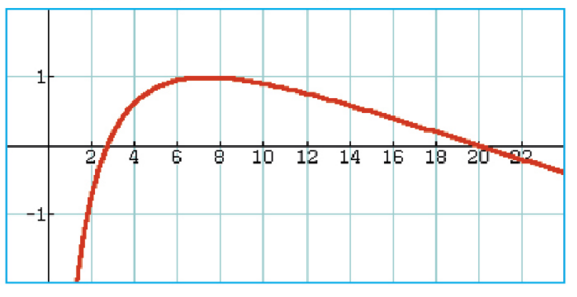
A l’aide de la calculatrice, on a affiché la courbe représentative de la fonction f définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par
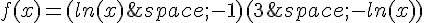
a) Déterminer l’abscisse de chacun des points d’intersection de cette courbe avec l’axe des abscisses.
b) Étudier le signe de la fonction f sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) .
.
Exercice 31 :
Résoudre les équations suivantes :
a) 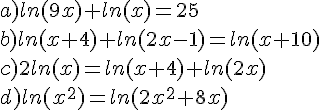
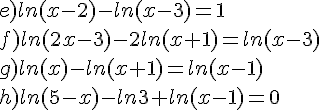
Exercice 32 :
f est la fonction définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par :
par :
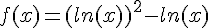
1.Étudier la limite de f en 0.
2.a) Vérifier que l’étude de la limite de f en  conduit à une forme indéterminée.
conduit à une forme indéterminée.
b) Pour tout 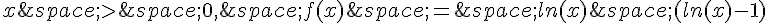
En déduire la limite de f en  .
.
Exercice 33 :
g est la fonction définie sur ![]1;+\infty[](https://mathovore.fr/latex-images/6231b6fcbed632976df3d0f3e8f461bb.png) par :
par :
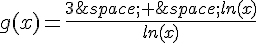
a) Quel est le signe de ln(x) lorsque 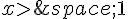 ?
?
b) En déduire la limite de g en 1.
2. Expliquer pourquoi pour tout réel 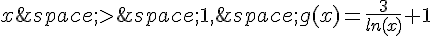
En déduire la limite de g en  .
.
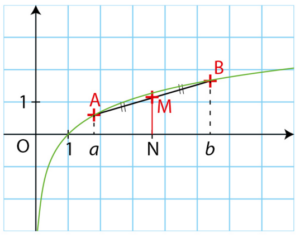
Exercice 34 :
Dans un repère orthonormé, A et B sont deux points de la courbe représentative de la
fonction 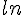 d’abscisses respectives a et b.
d’abscisses respectives a et b.
M est le milieu du segment [AB] et N est le projeté orthogonal de M sur l’axe des
abscisses.
Démontrer que 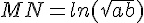 .
.
Exercice 35 :
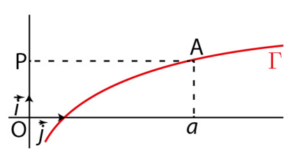
a désigne un nombre réel strictement positif. On note A le point d’abscisse a
de la courbe représentative de la fonction logarithme népérien dans un repère orthonormé 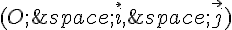 .
.
P est le projeté orthogonal du point A sur l’axe des ordonnées.
a) Q est le point d’intersection de la tangente T au point A à la courbe 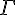 ‘ et de l’axe des ordonnées.
‘ et de l’axe des ordonnées.
Calculer la longueur PQ.
b) En déduire une construction simple de la tangente T.
Exercice 36 :
1.f est une fonction définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par 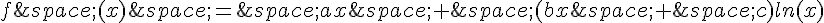
où a, b, c sont des réels.
La courbe représentative 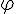 de f est donnée ci-dessous.
de f est donnée ci-dessous.
Utiliser les informations données sur le graphique pour déterminer a, b, c.
2. g est la fonction définie sur ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) par
par 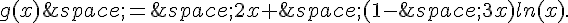
a) Étudier la limite de g en 0, puis en  .
.
b) Déterminer la fonction dérivée de g et étudier son signe en remarquant que 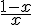
et  ont le même signe sur ]0 ; 1 [et sur
ont le même signe sur ]0 ; 1 [et sur ![]1;+\infty[](https://mathovore.fr/latex-images/6231b6fcbed632976df3d0f3e8f461bb.png) .
.
c) Dresser le tableau de variations de g.
Exercice 37 :
Le gain, en décibel (dB), d’une antenne parabolique de 1 m de diamètre peut se calculer par la formule :
G = 20 x 10 90
où f est la fréquence d’utilisation, en hertz (Hz).
a) Calculer le gain de l’antenne pour une fréquence d’utilisation de 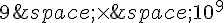 Hz.
Hz.
Arrondir au centième.
b) A partir de quelle fréquence peut-on utiliser une telle antenne sachant que le gain doit être supérieur
ou égal à 20 dB ? Arrondir à 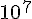 Hz.
Hz.
Exercice 38 :
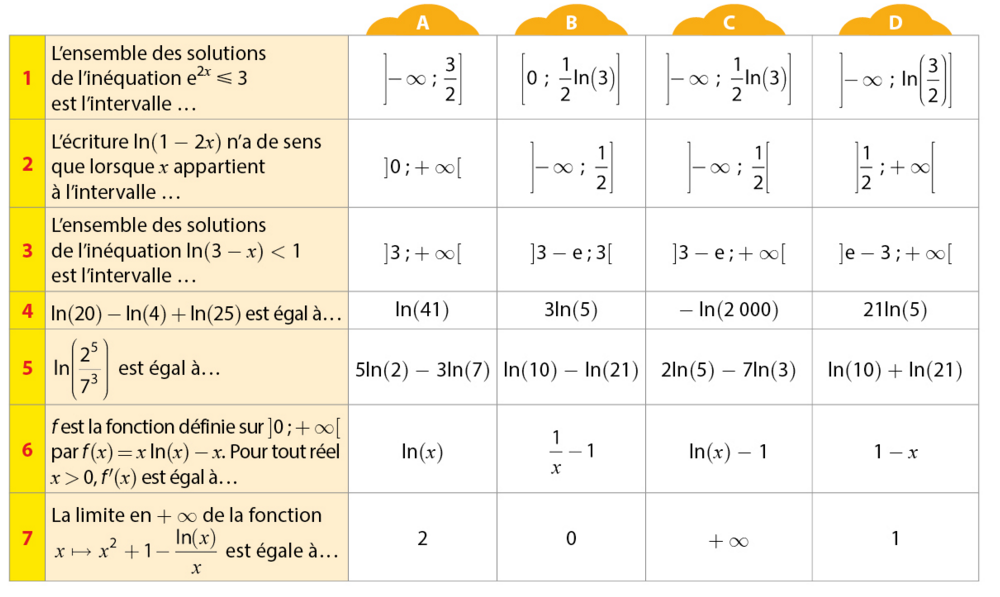
Effectuer les QCM sur les fonctions logarithmes suivants :
Exercice 39 :
Dans chaque cas, donner la (ou les) réponse(s) exacte(s) sans justifier.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «logarithmes : exercices de maths en terminale corrigés en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.