Les équations différentielles : exercices de maths en terminale.

Les équations différentielles à travers des exercices de maths en terminale corrigés.

Exercice 1 – Equations différentielles et condition initiale

Résoudre les équations différentielles suivantes :

1. $y'+5y=3\,et\,y(0)=0.$

2. $y'=-3y+4e^x\,et\,y(0)=-2.$

3. $y'+y=xe^{-x}+1\,et\,y(1)=0.$

4. $2y'+4y=6x^3+4x+2\,et\,y(0)=-\frac{9}{4}.$

Exercice 2 – Problème sur les équations différentielles
Soit (E) l’équation différentielle et $(E_0)\,\,y'-2y=0.$

1. Vérifier que la fonction définie par est solution de (E) .

2. Résoudre l’équation différentielle (Eo) .

3. Montrer que u est solution de (E) $\Leftrightarrow u-u_0$ est solution de (Eo) .

4. En déduire les solutions de (E) .

5. Déterminer la solution f de (E) qui s’annule en 1 .

Exercice 3 – Déterminer la solution d’une équation différentielle
Déterminer la solution de 2y ‘ + y = 1 telle que y(1) = 2 .

Exercice 4 – Résoudre cette équation différentielle

Résoudre l’équation différentielle 2y ‘ + y = 1

Exercice 5 – Premier ordre
1. Résoudre l’équation différentielle(E) : y ‘ = – 2y .

2. En déduire la solution de (E) dont la courbe représentative admet, au point d’abscisse 0,
une tangente parallèle à la droite d’équation y = – 4x + 1.

Exercice 6 – Equation différentielle du premier ordre

1. Résoudre l’équation différentielle (E) : y ‘ = 3y .

2. Déterminer la solution de (E) dont la courbe représentative passe par le point de coordonnées (2; 3).

Exercice 7 – Second membre variable

On considère l’équation différentielle .

1.Résoudre sur $\mathbb{R}$ l’équation sans second membre associé : .

2. Déterminer des réels a et b de sorte que la fonction p définie sur $\mathbb{R}$ par soit solution de (E) sur $\mathbb{R}$ .

3.Démontrer que f est une solution de (E) sur $\mathbb{R}$ si et seulement si est une solution de sur $\mathbb{R}$ .

4.En déduire les solutions de (E) sur R.

Exercice 8 – Application du cours

1.Résoudre sur $\mathbb{R}$ chacune des équations différentielles suivantes :

$y'=y\\4y'+y=0\\y'-3y=2$

2.On considère l’équation différentielle : .

Déterminer la solution de (E) sur $\mathbb{R}$ dont la courbe passe par le point A(0;3) dans un repère du plan.

Exercice 9 – Extraits du baccalauréat s

On considère l’équation différentielle $y'-2y=e^{2x} (E)$ .

1. Démontrer que la fonction u définie sur $\mathbb{R}$ par $u(x)=xe^{2x}$ est une solution de (E) .

2. Résoudre l’équation différentielle $y'-2y=0 \,\,(E_0)$ .

3. Démontrer qu’une fonction v définie sur $\mathbb{R}$ est solution de (E) si et seulement si v-u est solution de .

4. En déduire toutes les solutions de l’équation (E) .

5. Déterminer la fonction, solution de (E), qui prend la valeur 1 en 0 .

6. Le plan est muni d’un repère orthonormé $(O,\vec{i},\vec{j}).$

Soit la fonction f définie sur $\mathbb{R}$ par $f(x)=(x+1)e^{2x}$ .

On note C la courbe représentative de f dans le repère $(O,\vec{i},\vec{j}).$

a. Etudier les variations de f puis dresser son tableau de variation .

b. Tracer C .

Exercice 10 – Etude d’une température
On désigne par q(t) la température (exprimée en degré Celsius) d’un corps à l’instant t (exprimé
en heure).

A l’instant t = 0 , ce corps dont la température est de 100 °C est placé dans une salle à 20 °C.

D’après la loi de refroidissement de Newton, la vitesse de refroidissement q ‘ (t) est
proportionnelle à la différence entre la température du corps et celle de la salle.

On suppose que le coefficient de refroidissement est – 2, 08 .

1. Justifier que q ‘ (t) = – 2 , 08q(t) + 41,6 .

2. En déduire l’expression de q(t) .

3. Déterminer le sens de variation de la fonction q sur $[0;+\infty[.$

4. Calculer la limite de q en $+\infty.$
Interpréter ce résultat.

5. Déterminer la température du corps, arrondie au degré, au bout de 20 minutes puis au
bout de 30 minutes.

6. Déterminer la valeur exacte du temps au bout duquel le corps tombera à 30 °C.

En donner une valeur approchée.

Exercice 11 :

(E) est l’équation différentielle $y'\,-\,7y=\,0$ .
a) Résoudre l’équation différentielle (E).
b) Déterminer la solution f de (E) vérifiant la condition f(0) = 2.

Exercice 12 :

(E) est l’équation différentielle $y'\,=5y\,+\,2$ .
a) Déterminer la fonction constante f solution particulière de (E).
b) Démontrer qu’une fonction g est solution de (E) si, et seulement si, $g\,-\,f$ est solution de $y'\,=\,5y$ .
c) En déduire l’ensemble des solutions sur $\mathbb{R}$ de (E).
d) Déterminer la solution h de (E) dont la courbe représentative $(\,\varphi\,)$ dans un repère orthonormé admet une tangente au point d’abscisse de coefficient directeur 2.

Exercice 13 :

F et G sont deux fonctions définies sur $\mathbb{R}$ par :
$F(x)=\frac{8-e^x}{e^x+2}$ et $G(x)=\frac{-5e^x}{e^x+2}+3$ .

a) Déterminer $F(x)-\,G(x)$ pour tout réel x.
b) Dans une phrase utilisant le mot « primitive », tirer une conséquence de a) pour F et G.

Exercice 14 :

f est la solution sur $\mathbb{R}$ de l’équation différentielle $y'=\,3y$ telle que $f'(1)=\,2$ .

Justifier que $f(1)=\frac{2}{3}$ ,puis déterminer la fonction f.

Exercice 15 :

Déterminer la solution g sur $\mathbb{R}$ de l’équation différentielle $2y'+5y=\,0$ telle que $g\,'(2)\,=0$ .

Exercice 16 :

f est la fonction définie sur $\mathbb{R}$ par $f(x)\,=5e^{-4x}$ .
Déterminer l’équation différentielle de la forme $y'=\,ay$ dont f est une solution sur $\mathbb{R}$ .

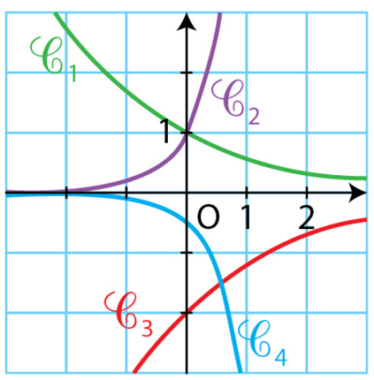
Exercice 17 :

Dans ce repère, les courbes représentent des solutions d’équations différentielles du type .
Associer chacune de ces courbes à l’équation différentielle $(E_1)\,:\,y'=2y$ ou $(E_2)\,:\,y'+0,5y=0$ .

Exercice 18 :

Pour déterminer l’âge de résidus organiques, on utilise la méthode basée sur la désintégration radioactive.

Les êtres vivants absorbent et assimilent du carbone de l’atmosphère.

On considère que leur organisme comporte une proportion constante de carbone 14.
Après leur mort, cette proportion de carbone 14 diminue lentement.
m est la fonction qui donne la masse résiduelle m(t), en g, de carbone 14 dans un échantillon à la date t, en siècle.

La vitesse de désintégration du carbone 14 à la date t est proportionnelle à la masse à cet instant.
Ainsi, il existe un réel C tel que $m'(t)\,=\,C\,\times \,m(t)$ .
Un corps organique contenait une masse mo de carbone 14 à l’instant $t\,=0$ de sa mort.
a) Exprimer m(t) en fonction de C et .
b) On sait que la masse de carbone 14 dans un échantillon diminue de 1,24 % par siècle.
En déduire la valeur de C.
c) Aujourd’hui, ce corps organique ne contient plus que 14 % de sa masse de carbone 14.
Déterminer l’âge de ce corps. Arrondir au centième.

Exercice 19 :

Un chariot de masse 200 kg se déplace à partir d’une origine O sur une voie rectiligne et horizontale.
est la distance, en mètre, qui le sépare de l’origine en fonction du temps t, en seconde ( $t\,\geq\,\,0$ ).
D’après les lois de Newton, la fonction x vérifie $200x''+\,25x'\,=\,50$ où $x\,''$ est la dérivée de la fonction
dérivée par rapport au temps t.

1. Déterminer x(0).
2. v(t) est la vitesse du chariot à l’instant t et vérifie $v(t)\,=\,x'(t)$ .

a) Démontrer que x vérifie $200x''+\,25x'\,=\,50$ si, et seulement si, la fonction v vérifie $v'\,=\,-\,0,125v\,+\,0,25$ .

b) Résoudre sur $[0\,;\,+\infty[$ l’équation différentielle :
$y'=\,-\,0,125y\,+\,0,25$ .

c) La vitesse initiale du chariot est supposée nulle, ainsi .
Déterminer alors la vitesse pour tout réel t.

d) Étudier la limite de v en $+\infty$ et interpréter le résultat.
3. a) Démontrer alors que la fonction x est définie sur l’intervalle $[0\,;\,+\infty[$ par :

$x(t)=\,2t-\,16+\,16e^{-0,125t}$

b) Quelle est la distance, en m, parcourue par le chariot au bout de 30 secondes ?

Arrondir au dixième.

4.2/5 - (23 votes)

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les équations différentielles : exercices de maths en terminale corrigés en PDF.» au format PDF.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Les équations différentielles : exercices de maths en terminale corrigés en PDF.

Télécharger et imprimer ce document en PDF gratuitement :

D'autres cours et exercices à consulter

Télécharger et imprimer ce document en PDF gratuitement :

D'autres cours et exercices à consulter

Cours de terminale

Exercices de terminale

Baccalauréat

Nos applications