Suite de matrices : cours de maths en terminale spécialité en PDF.

Mis à jour le 4 avril 2025

Sommaire

🧮Cours de Mathématiques

Terminale • Lycée

Suite de matrices

📖 Temps de lecture : 5 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les suites de matrices à travers un cours de maths en terminale spécialité où nous étudierons des suites convergentes vers une autre matrice.

I.Suite de nombres (Un) vérifiant 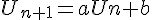$U_{n+1}=aUn+b$ .

Une telle suite est dite arithmético-géométrique (ou à récurrence affine).

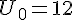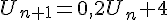Etudions un exemple.La suite (Un) est définie par et pour tout entier naturel n, $U_{n+1}=0,2U_n+4$ .

1. De la formule de récurrence à la formule explicite.

Observons que si la suite (Un) converge, alors sa limite x est solution de l’équation x=0,2x+4.

Cette équation a pour solution x=5.Cela suggère de poser : pour tout entier naturel n, .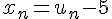

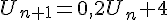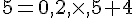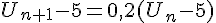De $U_{n+1}=0,2U_n+4$ et $5=0,2,\times ,5+4$ , on déduit par soustraction : $U_{n+1}-5=0,2(U_n-5)$ .

Soit 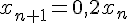$x_{n+1}=0,2x_n$ .La suite 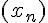est géométrique de raison a = 0,2 et de premier terme .

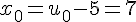D’où pour tout entier naturel n, 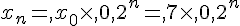$x_{n}=,x_0\times ,0,2^n=,7\times ,0,2^n$ .

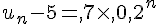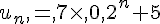Ainsi $u_n-5=,7\times ,0,2^n$ donc $u_n,=,7\times ,0,2^n+5$ .

2.Méthode générale : détermination d’une formule explicite.

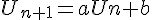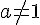On considère une suite de nombre (Un) qui vérifie $U_{n+1}=aUn+b$ , avec $a\neq1$ .

On résoud l’équation 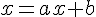: elle a une solution unique c.
On introduit la suite auxiliaire 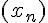définie par 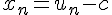.On prouve qu’elle est géométrique de raison a.; il en résulte que pour tout naturel n, .
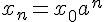On revient à la suite initiale : pour tout entier naturel n, 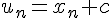.D’où l’expression :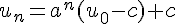

3.Etude de la convergence

Sur notre exemple, la raison a=0,2 est telle que – 1<a<1 donc 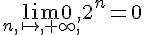$\lim_{n,\mapsto ,+\infty,}0,2^n=0$ .

Ainsi, 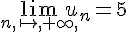$\lim_{n,\mapsto ,+\infty,}u_n=5$ .

Si on applique cette méthode dans le cas général, on obtient le résultat suivant :

Théorème :

Une suite de nombres (Un) vérifie 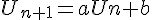$U_{n+1}=aUn+b$ , avec -1<a<1.

Alors la suite (Un) converge vers le nombre c vérifiant c = ac+b.

Ce résultat découle de la formule explicite et de la condition -1<a<1, car alors, 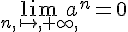$\lim_{n,\mapsto ,+\infty,}a^n=0$ .

Remarque :

On démontre que, si 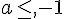$a\leq\,,-1$ ou a>1, la suite est divergente (hormis le cas particuliers où 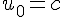, auquel cas elle est constante.

II.Suite de matrices colonnes (Un) vérifiant 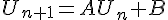$U_{n+1}=AU_n+B$ .

Etudions un exemple.La suite de matrices colonne (Un) de format (2,1) est définie par :

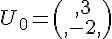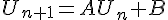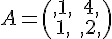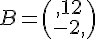$U_0=\begin{pmatrix},3\\,-2,\end{pmatrix}$ et pour tout entier naturel n, $U_{n+1}=AU_n+B$ où $A=\begin{pmatrix},1,4,\\1,,2,\end{pmatrix}$ et $B=\begin{pmatrix},12\\-2,\end{pmatrix}$ .

1.De la formule de récurrence à la formule explicite.

Inspirons-nous de la méthode précédente.Cherchons une matrice colonne C de format (2,1), telle que C=AC+B.Cette équation d’inconnue C s’écrit C-AC=B, c’est-à-dire (I-A)C=B.

Si I-A est inversible, multiplions à gauche les deux membres par 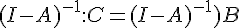$(I-A)^{-1}:C=(I-A)^{-1})B$ .

Or 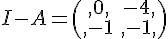$I-A=\begin{pmatrix},0,-4,\\,-1,-1,\end{pmatrix}$ ,cette matrice est inversible et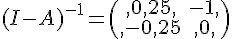 $(I-A)^{-1}=\begin{pmatrix},0,25,-1,\\,-0,25,0,\end{pmatrix}$

donc 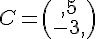$C=\begin{pmatrix},5\\-3,\end{pmatrix}$ .

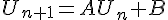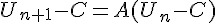De $U_{n+1}=AU_n+B$ et C=AC+B, on déduit par soustraction : $U_{n+1}-C=A(U_n-C)$ .

Poson alors, pour tout entier naturel n, 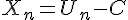; on obient 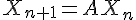$X_{n+1}=AX_n$ (1).

Démontrons par récurrence que l’égalité 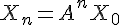$X_{n}=A^nX_0$ (2) est vraie pour tout entier naturel n.

Pour n=0, l’égalité (2) est vraie car .
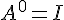Si 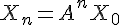$X_{n}=A^nX_0$ alors en multipliant à gauche les deux membres par 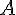, on obtient 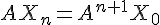$AX_{n}=A^{n+1}X_0$ , c’est-à-dire d’après (1), 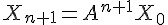$X_{n+1}=A^{n+1}X_0$ .Ainsi, l’égalité (2) est héréditaire.
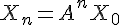On conclut que pour tout entier naturel n, $X_{n}=A^nX_0$ .

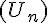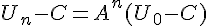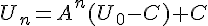Revenons à la suite : pour tout entier naturel n, $U_{n}-C=A^n(U_0-C)$ d’où $U_{n}=A^n(U_0-C)+C$ .

2. Méthode générale : détermination d’une formule explicite.

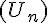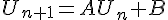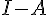Une suite de matrices colonnes (U_n) vérifie $U_{n+1}=AU_n+B$ où I-A est inversible.

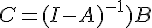On résout l’équation l’équation C=AC+B; elle admet une unique solution $C=(I-A)^{-1})B$ .
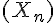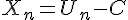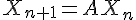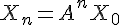On introduit la suite auxiliaire définie par .On prouve qu’elle vérifie, pour tout entier naturel n, $X_{n+1}=AX_n$ puis par récurrence que $X_{n}=A^nX_0$ .
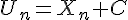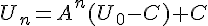On revient à la suite initiale: pour tout entier naturel n, .D’où l’expression $U_{n}=A^n(U_0-C)+C$ .

3. Suites de matrices lignes

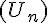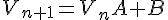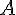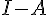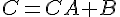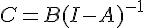Si est une suite de matrices lignes de même format telle que $V_{n+1}=V_nA+B$ , où est une matrice carrée et une matrice ligne, on obtient des résultats analogues : si est inversible, l’équation a une solution unique $C=B(I-A)^{-1}$ .

Alors pour tout naturel n, 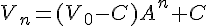$V_{n}=(V_0-C)A^n+C$ .

III. Convergence d’une suite de matrice

Définition :

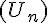(U_n) est une suite de matrices de format donné, L est une matrice de même format.Dire que la suite 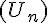(U_n) a pour limite L, signifie que, pour chaque emplacement, la suite des coefficients de 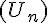(U_n) a pour limite le coefficient de L.

On dit aussi que 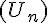converge vers L.

Exemple :

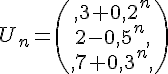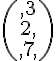$U_n=\begin{pmatrix},3+0,2^n\\2-0,5^n,\\,7+0,3^n,\end{pmatrix}$ converge vers la matrice $\begin{pmatrix},3\\2,\\,7,\end{pmatrix}$ .

4.2/5 - (23908 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «suite de matrices : cours de maths en terminale spécialité en PDF.» au format PDF.

Ressources de terminale

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Suite de matrices : cours de maths en terminale spécialité en PDF.

I.Suite de nombres (Un) vérifiant <img decoding="async" class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi?U_{n+1}=aUn+b" alt="U_{n+1}=aUn+b" />.