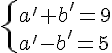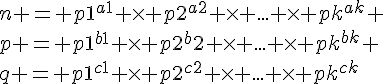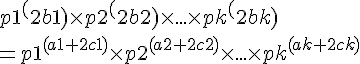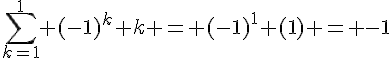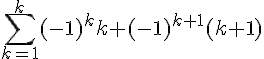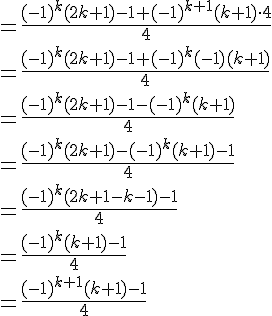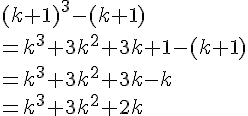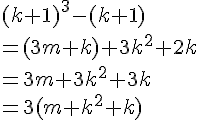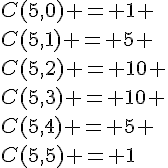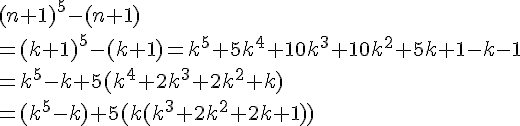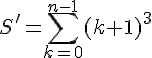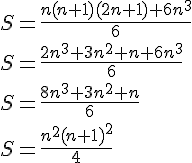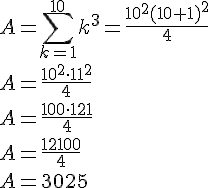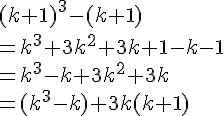Arithmétique : corrigé des exercices en terminale spécialité en PDF.

Exercice 1 :
1-Posons d = pgcd(a,b)
On a si d divise a et d divise b alors d divise b et d divise (a-bq)
Réciproquement : si d divise b et d divise (a-bq) alors d divise ( a – bq ) +bq = a
2- c’est la relation précédente avec .

Exercice 2 :

Pour démontrer que n(n+2)(n+4) est divisible par 3, on peut utiliser le principe de récurrence.

1. Vérification initiale :
Pour n = 1, on a , qui est divisible par 3.

2. Hypothèse de récurrence :
Supposons que pour un certain entier naturel k, est divisible par 3.

3. Étape de récurrence :
Nous devons démontrer que est aussi divisible par 3.

Développons cette expression littérale :

Nous pouvons remarquer que est divisible par 3 car chaque terme est divisible par 3.

De plus, 15 est également divisible par 3.

Donc, est divisible par 3.

4. Conclusion :
En utilisant le principe de récurrence, nous avons montré que pour tout entier naturel n, n(n+2)(n+4) est divisible par 3.

Exercice 3 :
Soit δ = PGCD(a ;b) et µ = PPCM(a ;b).

On a alors a= δa’ et b = δb’ avec a’ et b’ premiers entre eux.

On a donc PPCM(a’ ;b’) = a’b’

µ = PPCM(δa’ ; δb’) = δ×PPCM(a’ ; b’) = δ×a’×b’

Ainsi δµ = δ²×a’×b’ = δ×a’× δ×b’ = ab
Système d’équations et arithmétique.
De la relation PPCM(a;b)×PGCD(a;b) = ab,
on déduit à partir de la deuxième équation du système :

3×PPCM(a ;b) = PGCD(a ;b)×PPCM(a ;b)

Donc PGCD(a;b) = 3

Il existe alors des entiers a’ et b’ (premiers entre eux) tels que a = 3a’ et b = 3b’.

En reportant dans la première équation, on obtient :

9a’² – 9b’² = 405
Soit (a’ + b’)(a’ – b’) = 45
Or 45 = 3²×5
On peut donc avoir les 3 systèmes suivants :

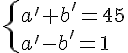
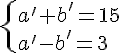
$\{ a' + b' = 45\\ a' -b' = 1 .$ $\{ a' + b' = 15\\ a' -b' = 3 .$ $\{ a' + b' = 9\\ a' -b' = 5 .$

a’ = 23 et b’ = 22 a’ = 9 et b’ = 6 a’ = 7 et b’ = 2

D’où (a ;b) = (66 ;69) ne convient pas car d’où (a ;b) = (42 ;6)
9 et 6 ne sont pas premiers entre eux

Les couples solutions du système sont donc (42 ;6) et (66 ;69).

Exercice 4 :

Pour résoudre le système d’équations donné, nous allons utiliser une approche par factorisation.

Équation 1:
Cette équation est une différence de carrés, donc nous pouvons factoriser le côté gauche en utilisant l’identité :

Équation 2: $3 \times ppcm(a,b) = ab$
La ppcm (plus petit commun multiple) de deux entiers a et b est le plus petit multiple commun à ces deux nombres.

Maintenant, nous allons résoudre le système d’équations en utilisant la factorisation de l’équation 1.

(a + b)(a – b) = 405

Pour simplifier les choses, nous allons noter (a + b) comme x et (a – b) comme y:
xy = 405

Ensuite, nous pouvons exprimer la deuxième équation en termes de x et y:
$3 \times ppcm((x + y)/2, (x - y)/2) = ((x + y)/2) \times ((x - y)/2)$

Simplifions cette équation en mettant tout sur un seul côté:
$(x + y) / 2 \times (x - y) / 2 - 3 \times ((x + y) / 2) \times ((x - y) / 2) = 0$

Donc, nous avons maintenant le système d’équations suivant:
xy = 405
$(x + y)/2 \times (x - y)/2 - 3 \times ((x + y)/2) \times ((x - y)/2) = 0$

En résolvant ce système d’équations, nous obtiendrons les valeurs possibles pour x (a + b) et y (a – b).

Comme 405 = 3 * 3 * 3 * 5 * 9, nous pouvons essayer différentes combinaisons de diviseurs de 405 qui multiplient pour donner 405. Les paires possibles de diviseurs comprennent: (1, 405), (3, 135), (5, 81), (9, 45).
Nous pouvons utiliser ces paires pour résoudre les équations.

1. Lorsque x = 405 et y = 1 :
(a + b) = 405 et (a – b) = 1
En résolvant ce système, nous obtenons a = 203 et b = 202.

2. Lorsque x = 135 et y = 3 :
(a + b) = 135 et (a – b) = 3
En résolvant ce système, nous obtenons a = 69 et b = 66.

3. Lorsque x = 81 et y = 5 :
(a + b) = 81 et (a – b) = 5
En résolvant ce système, nous obtenons a = 43 et b = 38.

4. Lorsque x = 45 et y = 9 :
(a + b) = 45 et (a – b) = 9
En résolvant ce système, nous obtenons a = 27 et b = 18.

Donc, les solutions dans ℕ pour le système d’équations sont :
(a, b) = (203, 202), (69, 66), (43, 38), (27, 18).

Exercice 5 :
1)

$(a + b)^2 + b^2\geq\, 4\,et\,(a - b)^2 + b^2\geq\, 4.$ car a et b sont supérieurs ou égaux à 2.

est le produit de deux entiers supérieurs strictement à 1.

Donc n’est pas un nombre premier.

Exercice 7 :

1. Démonstration de :

Nous pouvons utiliser l’identité factorielle pour les cubes parfaits, qui dit que .

Posons a = x et b = y.

Alors:
.

Donc, l’identité est démontrée.

2. Résolution de l’équation x^3 – y^3 = 127 où les inconnues sont des entiers naturels :

Nous voulons trouver des entiers naturels x et y qui satisfont l’équation x^3 – y^3 = 127.

En utilisant l’identité factorielle démontrée précédemment, nous pouvons réécrire l’équation comme suit :
(x – y)(x^2 + xy + y^2) = 127.

Puisque 127 est un nombre premier, cela signifie que les seules façons d’exprimer 127 comme produit de deux facteurs est 1 * 127 ou -1 * -127.

Nous devons alors trouver des valeurs possibles pour x – y et x^2 + xy + y^2 qui donnent 127 lorsque multipliées.

En testant différentes valeurs possibles pour x – y, nous pouvons trouver des paires (x, y) qui satisfont l’équation. Voici quelques-unes des paires possibles qui donnent 127 :

Dans ce cas, nous pouvons résoudre les équations :

En résolvant ces équations, nous obtenons les solutions suivantes :
(x, y) = (6, 5) et (x, y) = (-20, -21)

Dans ce cas, nous pouvons résoudre les équations :

Cependant, nous recherchons des solutions dans les entiers naturels, donc ces paires ne sont pas valables.

Donc, les solutions entières naturelles de l’équation sont :

Exercice 8 :

Pour démontrer que le couple (q, r) est unique, nous allons utiliser la méthode de contradiction.

Supposons qu’il existe deux couples (q1, r1) et (q2, r2) qui satisfont les conditions du théorème de la division euclidienne pour a et b.
Cela signifie que nous avons :
a = bq1 + r1 et 0 ≤ r1 ≤ |b|,
a = bq2 + r2 et 0 ≤ r2 ≤ |b|.

Nous allons montrer que q1 = q2 et r1 = r2.

1. Montrons que q1 = q2 :
En soustrayant l’équation (a = bq1 + r1) de l’équation (a = bq2 + r2), nous obtenons :
0 = b(q2 – q1) + (r2 – r1).

Puisque 0 ≤ r1, r2 ≤ |b|, cela signifie que |r2 – r1| ≤ |b|.
De plus, puisque b(q2 – q1) est un multiple de b, |b(q2 – q1)| est également inférieur ou égal à |b|.

Donc, nous avons $|b(q2 - q1) + (r2 - r1)| \leq\, |b| + |b| = 2|b|.$
Cela signifie que la différence (q2 – q1) est un entier dont la valeur absolue est inférieure ou égale à 2.

Mais comme q1 et q2 sont tous les deux des entiers, il n’y a que trois possibilités pour leur différence (q2 – q1) : -2, 0, ou 2.
Cela implique que q2 – q1 = 0, ce qui signifie que q1 = q2.

2. Montrons que r1 = r2 :
En utilisant l’égalité q1 = q2, nous pouvons réécrire l’équation (a = bq1 + r1) comme suit :
a = bq2 + r1.

En soustrayant l’équation (a = bq2 + r2) de cette nouvelle équation, nous obtenons :
0 = (r1 – r2).

Puisque r1 et r2 sont tous les deux des nombres naturels, cela signifie que r1 – r2 = 0 et donc r1 = r2.

Ainsi, nous avons montré que si deux couples (q1, r1) et (q2, r2) satisfont les conditions du théorème de la division euclidienne pour a et b, alors q1 = q2 et r1 = r2.

Cela implique que le couple (q, r) est unique.

Exercice 9 :

1. Pour exprimer p^2 en fonction de n et q, nous élevons au carré les deux côtés de l’équation sqrt(n) = p/q :
$( \sqrt{n} )^2 = (\frac{p}{q})^2$

Cela donne $n = \frac{p^2 }{ q^2}$ .

En multipliant les deux côtés de cette équation par q^2, nous obtenons :
$n \times q^2 = p^2$ .

Donc, $p^2 = n \times q^2$ .

2. En utilisant la décomposition en facteurs premiers, nous pouvons écrire n, p et q de la manière suivante :
$n = p1^{a1} \times p2^{a2} \times ... \times pk^{ak} \\\\p = p1^{b1} \times p2^b2 \times ... \times pk^{bk} \\\\q = p1^{c1} \times p2^{c2} \times ... \times pk^{ck}$

où les pi sont des nombres premiers distincts et les ai, bi, ci sont des entiers positifs.

En substituant ces expressions dans l’équation p^2 = n * q^2, nous obtenons :
$(p1^{b1} \times p2^{b2} \times ... \times pk^{bk})^2 = (p1^{a1} \times p2^{a2} \times ... \times pk^{ak}) \times (p1^{c1} \times p2^{c2} \times ... \times pk^{ck})^2$

En simplifiant cette équation, nous obtenons :
$p1^({2b1}) \times p2^({2b2}) \times ... \times pk^({2bk})\\\\ = p1^{(a1 + 2c1)} \times p2^{(a2 + 2c2) }\times ... \times pk^{(ak + 2ck)}$

Cela signifie que pour chaque pi, les exposants des facteurs premiers correspondants doivent être égaux.

Maintenant, supposons qu’il existe un pi, par exemple p1, dont l’exposant de p dans p^2 est différent de l’exposant correspondant de pi dans n * q^2.

Ce serait une contradiction avec le fait que tout entier naturel admet une décomposition unique en produit de facteurs premiers.

Par conséquent, les exposants des facteurs premiers dans la décomposition de n sont les mêmes que les exposants des facteurs premiers dans la décomposition de p^2.

3. En conclusion, si $\sqrt{ n }$ est un nombre rationnel, alors nous pouvons l’exprimer sous la forme p/q, où p et q sont des entiers avec .

En utilisant cette expression, nous avons montré que $p^2 = n \times q^2$ et que les exposants des facteurs premiers dans la décomposition de n sont les mêmes que les exposants des facteurs premiers dans la décomposition de .

Cela signifie que si n est le carré d’aucun entier, alors les exposants des facteurs premiers dans la décomposition de n doivent tous être pairs.

4. Pour démontrer que sqrt(2) + sqrt(3) n’est pas un nombre rationnel, nous allons utiliser la méthode de l’absurde.

Supposons que $\sqrt(2) + \sqrt(3)$ est un nombre rationnel, c’est-à-dire qu’il peut être exprimé sous la forme p/q où p et q sont des entiers avec pgcd(p,q)=1.

En élevant au carré les deux côtés de l’équation, nous obtenons :
$( \sqrt{2} + \sqrt{3})^2 = (\frac{p}{ q})^2$

Cela donne $2 + 2 \sqrt{6} + 3 = p^2/q^2$

En simplifiant cette équation, nous obtenons :
$5 + 2 \sqrt{6} = p^2/q^2$

Cela impliquerait que √6 est un nombre rationnel, ce qui est une contradiction avec le fait que √6 ne peut pas être exprimé sous la forme p/q où p et q sont des entiers avec pgcd(p,q)=1.

Par conséquent, nous avons montré que $\sqrt{ 2} + \sqrt{3}$ n’est pas un nombre rationnel.

Exercice 11 :

Nous allons démontrer cette égalité par récurrence.

Pour n = 1, l’équation devient :

$\sum_{k=1}^{1} (-1)^k k = (-1)^1 (1) = -1$

De plus, $\frac{(-1)^1(2(1)+1)-1}{4} = \frac{-1}{4}$ , ce qui est égal à -1.

Donc la formule est vérifiée pour n = 1.

Supposons maintenant que la formule soit vraie pour un certain entier k, c’est-à-dire :

$\sum_{k=1}^{k} (-1)^k k = \frac{(-1)^k(2k+1)-1}{4}$

Nous allons montrer que la formule est également vraie pour n = k+1.

Considérons l’expression 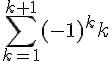$\sum_{k=1}^{k+1} (-1)^k k$ . On peut la réécrire comme :

$\sum_{k=1}^{k} (-1)^k k + (-1)^{k+1} (k+1)$

D’après notre hypothèse de récurrence, nous savons que 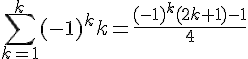$\sum_{k=1}^{k} (-1)^k k = \frac{(-1)^k(2k+1)-1}{4}$ , nous pouvons donc réécrire l’expression :

$\frac{(-1)^k(2k+1)-1}{4} + (-1)^{k+1} (k+1)$

Simplifions cette expression :

$\\\\= \frac{(-1)^k(2k+1)-1+(-1)^{k+1} (k+1)\cdot 4}{4} \\\\= \frac{(-1)^k(2k+1)-1+(-1)^k (-1)(k+1)}{4} \\\\= \frac{(-1)^k(2k+1)-1-(-1)^k (k+1)}{4} \\\\= \frac{(-1)^k(2k+1)-(-1)^k (k+1)-1}{4} \\\\= \frac{(-1)^k(2k+1 - k - 1)-1}{4} \\\\= \frac{(-1)^k(k+1)-1}{4} \\\\= \frac{(-1)^{k+1}(k+1)-1}{4}$

On a donc montré que si la formule est vraie pour n = k, alors elle est également vraie pour n = k+1.

Ainsi, la formule est vérifiée pour tous les entiers n \geq\, 1, par récurrence.

Exercice 12 :

Nous allons démontrer cette inégalité par récurrence.

Pour n = 0, l’inégalité devient $(1+x)^0 \geq\, 1 + 0x = 1$ .

L’inégalité est vraie pour n = 0 car est égal à 1.

Supposons maintenant que l’inégalité soit vraie pour un certain entier k, c’est-à-dire :

$(1+x)^k \geq\, 1 + kx$

Nous allons montrer que l’inégalité est également vraie pour n = k+1.

Considérons l’expression $(1+x)^{k+1}$ . On peut la réécrire en utilisant la formule du binôme de Newton :

$(1+x)^{k+1} = (1+x)^k \times (1+x)$

D’après notre hypothèse de récurrence, nous savons que $(1+x)^k \geq\, 1 + kx$ . Nous pouvons donc réécrire l’expression :

$(1+x)^{k+1} \geq\, (1 + kx) \times (1+x)$

Simplifions cette expression :

$(1+x)^{k+1} \geq\, 1 + x + kx + kx^2$
$(1+x)^{k+1} \geq\, 1 + (k+1)x + kx^2$

Puisque x est un réel positif, kx^2 est également positif. On peut donc écrire :

$(1+x)^{k+1} \geq\, 1 + (k+1)x$

On a donc montré que si l’inégalité est vraie pour n = k, alors elle est également vraie pour n = k+1.

Ainsi, l’inégalité est vérifiée pour tous les entiers $n \geq\, 0$ , par récurrence.

Exercice 13 :

1. La contraposée de la proposition précédente est :

Si n est impair, alors est divisible par 8.

2. Pour prouver la contraposée, nous supposons que n est impair, c’est-à-dire n = 2k + 1 pour un certain entier k.

Nous devons maintenant montrer que est divisible par 8. Nous remplaçons n dans l’expression n^2-1 pour obtenir :

Nous voyons que est un multiple de 8, car k^2 est un entier. De plus, 4k est également un multiple de 8, car 4k = 2(2k), où 2k est un entier.

Ainsi, nous pouvons écrire comme 8m, où m est l’entier .

Cela montre que si n est impair, alors est divisible par 8.

3. À partir de cette démonstration par contraposée, nous pouvons en déduire que si n’est pas divisible par 8, alors n n’est pas impair.

Autrement dit, si n est impair, alors est divisible par 8.

Cela signifie que si l’entier n’est pas divisible par 8, alors l’entier n est pair.

Exercice 14 :

Nous allons démontrer cette affirmation par récurrence.

Pour n = 0, nous avons .

Comme 0 est un multiple de 3, l’affirmation est vraie pour n = 0.

Supposons maintenant que l’affirmation soit vraie pour un certain entier k, c’est-à-dire que est un multiple de 3.

Nous allons montrer que l’affirmation est également vraie pour .

Considérons l’expression . En développant cette expression, nous obtenons :

$(k+1)^3 - (k+1) \\\\= k^3 + 3k^2 + 3k + 1 - (k+1) \\\\= k^3 + 3k^2 + 3k - k \\\\= k^3 + 3k^2 + 2k$

Par hypothèse de récurrence, nous savons que est un multiple de 3.

Nous pouvons donc écrire :

, où m est un entier.

En remplaçant cette expression dans , nous avons :

$(k+1)^3 - (k+1)\\\\ = (3m + k) + 3k^2 + 2k \\\\= 3m + 3k^2 + 3k \\\\= 3(m + k^2 + k)$

Nous voyons que est un multiple de 3, car il peut être écrit sous la forme 3(n), où n est l’entier .

Ainsi, nous avons montré que si l’affirmation est vraie pour n = k, alors elle est également vraie pour n = k+1.

Par conséquent, l’affirmation est vérifiée pour tous les entiers n ≥ 0, par récurrence.

Exercice 15 :

1. Pour développer l’expression , nous utilisons la formule du binôme de Newton :

$(n+1)^5 = C(5,0) \times n^5 + C(5,1)\times n^4\times (1^1) + C(5,2)\times n^3\times (1^2) + C(5,3)\times n^2\times (1^3) + C(5,4)\times n^1\times (1^4) + C(5,5)\times (1^5)$

Les coefficients binomiaux C(5,k) sont donnés par les coefficients du développement du binôme :

$C(5,0) = 1 \\C(5,1) = 5 \\C(5,2) = 10 \\C(5,3) = 10 \\C(5,4) = 5 \\C(5,5) = 1$

En substituant ces coefficients, nous obtenons :

2. Maintenant, pour démontrer que pour tout entier $n \geq\, 0, n^5 - n$ est un multiple de 5, nous devons factoriser l’expression :

Il suffit maintenant de montrer que l’un des facteurs (n-1), n ou est divisible par 5.

Pour n = 0, nous avons n = 0 et n^5 – n = 0 qui est divisible par 5.

Supposons maintenant que pour un certain entier k ≥ 0, k^5 – k est divisible par 5.

Considérons le cas de :

$(n+1)^5 - (n+1) \\\\= (k+1)^5 - (k+1) = k^5 + 5k^4 + 10k^3 + 10k^2 + 5k + 1 - k - 1 \\\\= k^5 - k + 5(k^4 + 2k^3 + 2k^2 + k) \\\\= (k^5 - k) + 5(k(k^3 + 2k^2 + 2k + 1))$

Par hypothèse de récurrence, nous savons que est divisible par 5.

De plus, le second terme est également divisible par 5, car k est un entier.

Ainsi, nous avons montré que est divisible par 5, ce qui implique que est également divisible par 5 pour tout entier n ≥ 0.

Par conséquent, est un multiple de 5 pour tout entier n ≥ 0.

Exercice 16 :

1. Pour montrer que 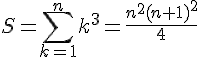$S = \sum_{k=1}^{n}k^3 = \frac{n^2(n+1)^2}{4}$ , nous pouvons utiliser la méthode de la somme télescopique.

Considérons la différence où S’ est la somme suivante :

$S' = \sum_{k=0}^{n-1}(k+1)^3$

Nous pouvons développer comme suit :

Remarquons que chaque terme de cette expression est présent dans la somme S. Cependant, le dernier terme (1) n’est pas présent dans S. Pour compenser cela, nous pouvons soustraire la somme S’ de S et obtenir :

Ainsi, nous avons .

Maintenant, réorganisons cette équation pour trouver S en fonction de S’ :

La somme S’ peut être simplifiée en utilisant la formule de la somme des premiers carrés :

La formule pour la somme des premiers carrés est donnée par :

$1 + 2^2 + 3^2 + ... + n^2 = \frac{n(n+1)(2n+1)}{6}$

Nous pouvons donc écrire :

$S' = \frac{n(n+1)(2n+1)}{6}$

En remplaçant cette expression dans la formule pour S, nous obtenons :

$S = \frac{n(n+1)(2n+1)}{6} + n^3$

Simplifions cette expression :

$S = \frac{n(n+1)(2n+1) + 6n^3}{6} \\\\S = \frac{2n^3 + 3n^2 + n + 6n^3}{6} \\\\S = \frac{8n^3 + 3n^2 + n}{6} \\\\S = \frac{n^2(n+1)^2}{4}$

Nous avons donc démontré que $\forall n \in \mathbb{N}^*, S = \sum_{k=1}^{n}k^3 = \frac{n^2(n+1)^2}{4}$ .

2. Pour trouver la valeur de , nous pouvons utiliser la formule que nous avons démontrée dans la question précédente :

$A = \sum_{k=1}^{10}k^3 = \frac{10^2(10+1)^2}{4} \\\\A = \frac{10^2 \cdot 11^2}{4} \\\\A = \frac{100 \cdot 121}{4} \\\\A = \frac{12100}{4} \\\\A = 3025$

Donc, A = 3025.

Exercice 17 :

Pour montrer que pour tout entier n ≥ 0, est un multiple de 3, nous pouvons utiliser une démonstration par récurrence.

1. Vérification de la propriété pour n = 0 :
Pour n = 0, on a , qui est un multiple de 3.

2. Supposons que la propriété est vraie pour un certain entier k ≥ 0, c’est-à-dire que est un multiple de 3.

3. Montrons que la propriété est également vraie pour k+1 :
$(k+1)^3 - (k+1)\\\\ = k^3 + 3k^2 + 3k + 1 - k - 1 \\\\= k^3 - k + 3k^2 + 3k \\\\= (k^3 - k) + 3k(k+1)$

Par hypothèse de récurrence, est un multiple de 3.

De plus, 3k(k+1) est également un multiple de 3, car k et k+1 sont tous deux des entiers.

Ainsi, nous avons montré que est un multiple de 3.

Par conséquent, par le principe de récurrence, nous pouvons conclure que pour tout entier $n \geq\, 0, n^3 - n$ est un multiple de 3.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «arithmétique : corrigé des exercices en terminale spécialité en PDF.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.