Conjugué, module et argument d’un nombre complexe : cours de maths en terminale en PDF.

Mis à jour le 1 octobre 2025

Sommaire

🧮Cours de Mathématiques

Terminale • Lycée

Conjugué, module et argument d’un nombre complexe

📖 Temps de lecture : 5 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les nombres complexes avec un cours de maths en terminale faisant intervenir la notion de conjugué et d’argument.

I. Conjugué d’un nombre complexe.

1. Définition du conjugué.

Définition :

Soit un nombre complexe de forme algébrique $z\,=\,x+iy$ (x, y réels).

Le nombre complexe $x\,-\,iy$ , noté $\,\overline{z}$ , est appelé conjugué du nombre complexe .

Exemples :

$\,\overline{2+3i}=2-3i$ ; $\,\overline{3}=3$ ; $\,\overline{-7}=-7$ ; $\,\overline{2i}=-2i$ ; $\,\overline{-5i}={5i}$ .

Conséquences :

$\,\overline{\,\overline{z}}=z$
$z\,\overline{z}=x^2+y^2$
$z+\,\overline{z}=2\times Re(z)=2x$
$z-\,\overline{z}=2\times Im(z)=2y$

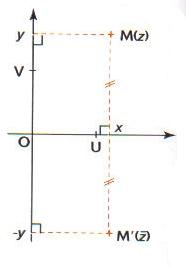
2. Interprétation géométrique.

Dans le plan complexe, considérons un point M d’affixe z alors le pont M’ d’affixe z est l’image de M par la symétrie par rapport à l’axe des réels (abscisses).

Propriétés :

Soit z un nombre complexe.

1. z est réel $\Longleftrightarrow z=\,\overline{z}$ .
2. z est imaginaire pur $\Longleftrightarrow z\,=\,-\,\,\overline{z}$ .

3. Conjugué et opérations.

Propriétés :

Soient z et z’ deux nombres complexes et n un entier naturel non nul.

$\,\overline{z+z\,#039;}=\,\overline{z}+\,\overline{z\,#039;}$

$\,\overline{zz\,#039;}=\,\overline{z}\,\overline{z\,#039;}$

$\,\overline{z^n}^n=\,\overline{z}^n$

$Si\, z\neq\,0 ,\, \,\,\overline{\frac{1}{z}}=\frac{1}{\,\overline{z}}$

$Si\, z\,#039;\neq\,0 ,\, \,\,\overline{\frac{z}{z\,#039;}}=\frac{\,\overline{z}}{\,\overline{z\,#039;}}$

II. Module et argument d’un nombre complexe.

1. Module d’un nombre complexe.

Définition :

Soit z un nombre complexe de forme algébrique x+iy (x et y réels).

Le module de z est le nombre réel positif noté $lzl=sqrt{x^2+y2}$ .

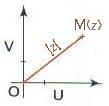
Interprétation géométrique :
Dans le plan complexe, si M a pour affixe z alors OM=lzl.

Remarque :

Si est un réel, le module de est égal à la valeur absolue de x.
$|z\,|=0$ si et seulement ( car équivaut à O=M)
$z\overline{z}=\,|\,z\,|^2$ .

2. Arguments d’un nombres complexe non nul.

Définition :

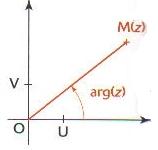
Soit un nombre complexe non nul, de point image M.

On appelle argument de et on note arg(z) , toute mesure en radian de l’angle orienté $(\vec{OU},\vec{OM})$ .

Remarque:
Un nombre complexe non nul z a une infinité d’argument; si $\theta$ est l’un d’entre eux alors tous les autres sont de la forme $\theta\,+\,2k\pi \,\,(k \in \mathbb{Z})$ .

On note $arg(z)=\,\theta\,[2\pi]$ ou plus simplement arg(z)= $\theta$

3. Forme trigonométrique d’un nombre complexe non nul.

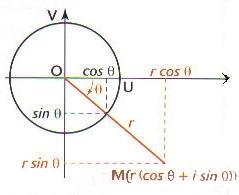
3.1. Repérages cartésien et polaire :

Dans le plan complexe un point M distinct de O peut être repéré par ses coordonnées cartésienne (x;y) ou par un couple $(r\,,\, \theta)$ de coordonnées polaires avec OM=r et $(\vec{OU}\,,\,\vec{OM})$ ,

on a alors :
$\fbox{\{{x\,=\,rcos\theta\atop y\,=\,rsin\theta}}$

3.2 Forme trigonométrique :

Définition :

Soit un nombre complexe non nul.

L’écriture $z\,=\,r(cos\theta\,+\,isin\theta)$ avec $r=\,|\,z\,|$ et $\theta\,\,=arg(z)$ est appelée forme trigonométrique de z.

Propriété :

Deux nombres complexes non nuls sont égaux si et seulement si, ils ont même module et même argument à un multiple de 2pi près.

Propriété :

Si $z\,=\,r(cos\theta\,+\,isin\theta)$ avec r>0 alors $r=\,|\,z\,|$ et $\theta\,\,=arg(z)$ .

4.3/5 - (20979 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «conjugué, module et argument d’un nombre complexe : cours de maths en terminale en PDF.» au format PDF.

Ressources de terminale

D'autres cours et exercices à consulter

Suite de matrices : cours de maths en terminale spécialité en PDF.

Fonctions sinus et cosinus : cours de maths en terminale en PDF.

Les probabilités conditionnelles : cours de maths en terminale en PDF.

Le raisonnement par récurrence : cours de maths en terminale en PDF.

Le théorème de Gauss : cours de maths en terminale spécialité en PDF.

Matrices et opérations : cours de maths en terminale spécialité en PDF.

Les suites numériques : cours de maths en terminale en PDF.

Le produit scalaire : cours de maths en terminale en PDF.

Exercices de maths interactifs avec saisie au clavier des réponses.

Maths et programmation dans un escape game.

Exercices de maths avec des patterns pour travailler les automatismes.

SCRATCH Dimension ; exercices de maths et de programmation avec scratch.

Exercices de géométrie sous forme d'escape game.

Calculus Arcana : escape game de calcul littéral.

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Conjugué, module et argument d’un nombre complexe : cours de maths en terminale en PDF.

I. Conjugué d’un nombre complexe.

1. Définition du conjugué.

2. Interprétation géométrique.

3. Conjugué et opérations.

II. Module et argument d’un nombre complexe.

1. Module d’un nombre complexe.

2. Arguments d’un nombres complexe non nul.

3. Forme trigonométrique d’un nombre complexe non nul.

3.1. Repérages cartésien et polaire :

3.2 Forme trigonométrique :

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

D'autres cours et exercices à consulter

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques