Bac maths 2024 aux centres étrangers : sujet n°2 corrigé

Bac de maths 2024 aux centres étrangers avec le sujet n° 2 et son corrigé. Ce sujet porte sur des probabilités et un sac opaque qui contient 8 jetons. Une étude d’une fonction rationnelle contenant une exponentielle avec étude de la dérivée, du sens de variation et de l’équation réduite d’une tangente en un point de sa courbe. De la géométrie dans l’espace avec l’étude de coordonnées de vecteurs et l’équation cartésienne d’un plan et l’équation paramétrique d’une droite. L’étude d’une fonction contenant une racine carrée et une suite récurrente. Vous devrez déterminer la limite de la suite et étudier un programme réalisé avec Python.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
Centres étrangers – SESSION 2024
MATHÉMATIQUES
Jour 2
Durée de l’épreuve : 4 heures

L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire « type collège » est autorisé.
La qualité de la rédaction, la clarté et la précision des raisonnements seront prises en
compte dans l’appréciation de la copie.

Les traces de recherche, même incomplètes ou infructueuses, seront valorisées.

Exercice 1 (5 points)
Un sac opaque contient huit jetons numérotés de 1 à 8, indiscernables au toucher.
À trois reprises, un joueur pioche un jeton dans ce sac, note son numéro, puis le remet dans
le sac.
Dans ce contexte, on appelle « tirage » la liste ordonnée des trois numéros obtenus.
Par exemple, si le joueur pioche le jeton numéro 4, puis le jeton numéro 5, puis le jeton
numéro 1, alors le tirage correspondant est (4 ; 5 ; 1).

1. Déterminer le nombre de tirages possibles.
2. a. Déterminer le nombre de tirages sans répétition de numéro.
b. En déduire le nombre de tirages contenant au moins une répétition de numéro.

On note la variable aléatoire égale au numéro du premier jeton pioché, celle égale au
numéro du deuxième jeton pioché et celle égale au numéro du troisième jeton pioché.
Puisqu’il s’agit d’un tirage avec remise, les variables aléatoires , et sont
indépendantes et suivent la même loi de probabilité.

3. Établir la loi de probabilité de la variable aléatoire .

4. Déterminer l’espérance de la variable aléatoire .

On note $S=\,X_1\,+\,X_2\,+\,X_3$ la variable aléatoire égale à la somme des numéros des trois
jetons piochés.
5. Déterminer l’espérance de la variable aléatoire .
6. Déterminer $P(S\,=\,24)$ .
7. Si un joueur obtient une somme supérieure ou égale à 22, alors il gagne un lot.
a. Justifier qu’il existe exactement 10 tirages permettant de gagner un lot.
b. En déduire la probabilité de gagner un lot.

Exercice 2 (6 points)
On considère la fonction définie sur l’intervalle $]-\infty;\,1[$ par $f(x)\,=\,\frac{e^x\,}{x-1}$ .
On admet que la fonction est dérivable sur l’intervalle $]-\infty;\,1[$ .
On appelle sa courbe représentative dans un repère.

1. a. Déterminer la limite de la fonction en 1.
b. En déduire une interprétation graphique.
2. Déterminer la limite de la fonction en $-\infty$ .
3. a. Montrer que pour tout réel de l’intervalle $]-\infty;\,1[$ , on a $f'(x)\,=\frac{(x-2)e^x}{(x-1)^2}$ .

b. Dresser, en justifiant, le tableau de variations de la fonction sur l’intervalle $]-\infty;\,1[$ .

4. On admet que pour tout réel de l’intervalle $]-\infty;\,1[$ , on a $f''(x)\,=\frac{(x^2-4x+5)e^x}{(x-1)^3}$ .

a. Étudier la convexité de la fonction sur l’intervalle $]-\infty;\,1[$ .

b. Déterminer l’équation réduite de la tangente T à la courbe au point d’abscisse 0.
c. En déduire que, pour tout réel de l’intervalle $]-\infty;\,1[$ , on a :
$e^x\,\geq\,\,(-2x\,-\,1)(x\,-\,1)$ .

5. a. Justifier que l’équation admet une unique solution $\alpha$ sur l’intervalle $]-\infty;\,1[$ .
b. À l’aide de la calculatrice, déterminer un encadrement de $\alpha$ d’amplitude $10^{-2}$ .

Exercice 3 (5 points)
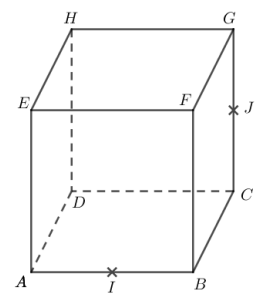
Le cube a pour arête 1 cm.
Le point est le milieu du segment [] et le point est le milieu du segment [].

On se place dans le repère orthonormé $(A\,;\vec{AB},\,\vec{AD}\,,\vec{AE})\,.$
1. Donner les coordonnées des points et .
2. Montrer que le vecteur $\vec{EJ}$ est normal au plan .
3. Montrer qu’une équation cartésienne du plan est $-\,2x-\,2y\,+\,z\,+\,1\,=\,0$ .
4. Déterminer une représentation paramétrique de la droite .
5. a. On note le projeté orthogonal du point sur le plan .
Calculer ses coordonnées.
b. Montrer que le volume de la pyramide est $\frac{1}{6}\,\,\,cm^3$ .

On pourra utiliser le point , milieu du segment . On admet que ce point est le
projeté orthogonal du point sur le plan .

c. Déduire des deux questions précédentes l’aire du triangle .

Exercice 4 (4 points)
Partie A
On considère la fonction définie sur l’intervalle $[0\,;\,+\infty[$ par $f(x)=\sqrt{x+1}$ .
On admet que cette fonction est dérivable sur ce même intervalle.

1. Démontrer que la fonction est croissante sur l’intervalle $[0\,;\,+\infty[$ .
2. Démontrer que pour tout nombre réel appartenant à l’intervalle $[0\,;\,+\infty[$ :
$f(x)-x=\frac{-x^2+x+1}{\sqrt{x+1}+x}$

3. En déduire que sur l’intervalle $[0\,;\,+\infty[$ l’équation admet pour unique solution :

$l=\frac{1+\sqrt{5}}{2}$ .

Partie B
On considère la suite définie par $u_0\,=\,5$ et pour tout entier naturel $n,\,u_{n+1}\,=\,f(u_n)$ où
est la fonction étudiée dans la partie A.

On admet que la suite de terme général est bien définie pour tout entier naturel .

1. Démontrer par récurrence que pour tout entier naturel , on a $1\,\leq\,\,u_{n+1}\,\leq\,\,u_n$ .
2. En déduire que la suite converge.
3. Démontrer que la suite converge vers $l=\frac{1+\sqrt{5}}{2}$ .
4. On considère le script Python ci-dessous :

On rappelle que la commande abs(x) renvoie la valeur absolue de x.

a. Donner la valeur renvoyée par seuil(2).
b. La valeur renvoyée par seuil(4)est 9.
Interpréter cette valeur dans le contexte de l’exercice

Consulter le corrigé

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac maths 2024 aux centres étrangers : sujet n°2 corrigé» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.