Les équations différentielles : cours de maths en terminale en PDF.
Mis à jour le 8 juillet 2025
Introduction
• Une équation différentielle est une équation dans laquelle l’inconnue est une fonction f.
De plus, cette équation fait intervenir la fonction f ainsi que ses dérivées successives, d’où le terme différentiel.
• Les équations différentielles apparaissent naturellement dans de nombreux domaines : physique, électricité, biologie,chimie, évolution des populations, modélisation informatique….
• En électricité , l’équilibre stationnaire d’un circuit électrique RLC(Résistance-Bobine) est traduit par l’équation : E = Ri(t) + L i'(t) où i est l’intensité du courant et t la variable temps.
• En sciences physiques encore, si N(t) désigne le nombre de noyaux désintégrés à l’instant t, l’expérience montre que N ‘(t) = -kN (t ) où k est une constante.
• La résolution de ces équations est donc fondamentale dans de nombreux domaines déjà rencontrées lors de la construction de la fonction exponentielle, nous étudierons en priorité les équations différentielles du type y’ = ay + b, où la fonction y est l’inconnue, et a et b sont deux réels.
I . Vocabulaire et généralités.
Dans une équation différentielle l’inconnue est une fonction, notée y en général.
L’équation est dite différentielle car elle fait intervenir les dérivées successives de la fonction y.
Rappelons en effet que la dérivée est associé à un taux de variation (ou croissance), qui est lui-même une différence (quotient des variations de y sur variation de x) : d’où le terme différentiel.
Résoudre l’équation différentielle y’ = ay + b c’est trouver toutes les fonctions f dérivables sur IR telles que pour tout x, f ’(x) = af(x) + b où a et b sont deux constantes (indépendant de x).
Précisons aussi que l’équation y’ = ay + b est dite du premier ordre car elle fait intervenir seulement la dérivée première.
Evidemment, il y des équations différentielles du 2ème ordre, du 3ème …
II . Résolution de y’ = ay, a constante réelle :
1. Les fonctions solutions de l’équation y’ = ay sont les fonctions définies su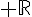r 
par .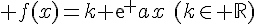
2. Il existe une unique fonction dérivable f telle que y’ = ay et 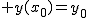: k est alors fixé par cette condition initiale.
Exercice :
a. Résoudre l’équation différentielle (E) : y’ = 3y.
b. Déterminer la solution de (E) dont la courbe représentative passe par le point de coordonnées A(2,3).
III .Résolution de y’ = ay + b, a (non nul) et b constantes réelles
Soit a un réel non nul.
• Les fonctions solutions de l’équation y’ = ay + b sont les fonctions définies su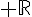r par .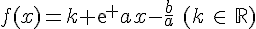
• Il existe une unique fonction dérivable f telle que y’ = ay + b et 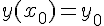( k est alors fixé par cette condition initiale).
Exercice sur les équations différentielles
Résoudre dans 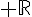, l’équation 2y’ + y = 1.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les équations différentielles : cours de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
