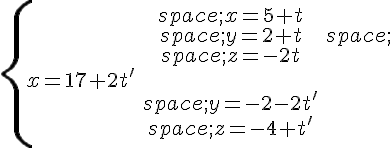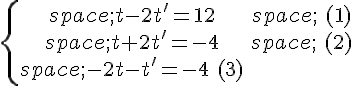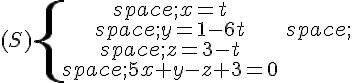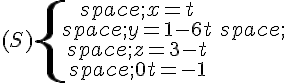Représentation paramétrique et équation cartésienne : cours de maths en terminale.

Les représentations paramétriques de droites et plans de l’espace, ainsi que, les équations cartésiennes à travers un cours de maths en terminale à télécharger en PDF.

Avec l’introduction des coordonnées dans un repère du plan. René Descartes fait basculer
des objets jusque-là purement géométriques (points, droites, segments, etc.) dans le domaine algébrique.

Ces objets peuvent désormais être décrits par leurs coordonnées ou leurs équations.
Mais la méthode de Descartes reste limitée au plan, c’est-à-dire à deux coordonnées.
Plus d’un siècle plus tard, vers 1760, Euler et Lagrange développent ces notions dans l’espace
et établissent les équations de droites et de plans de l’espace, en utilisant des repères à trois axes
de coordonnées.
Durant cette période, la géométrie analytique continue de se développer, notamment avec
Gaspard Monge, qui propose plusieurs mémoires à l’Académie des Sciences.

Il résout ainsi divers problèmes géométriques de manière analytique.

I. Représentations paramétriques d’une droite.

$(O\,;\,\vec{i},\,\vec{j},\,\vec{k})$ est un repère orthonormé de l’espace.

1.Principe.

Définition :

Soit (d) la droite qui passe par le point A de coordonnées $(x_A\,;\,y_A\,;\,z_A)$ et qui
admet pour vecteur directeur le vecteur $\vec{u}$ de coordonnées (a ; b ; c).

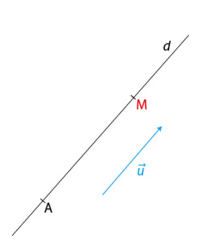
cours sur les représentations paramétriques et les équations cartésiennes

Dire qu’un point M de coordonnées $(x\,;y;\,z)$ appartient à (d), équivaut à dire
que les vecteurs $\vec{AM}$ et $\vec{u}$ sont colinéaires, c’est-à-dire qu’il existe un réel t tel
que $\vec{AM}\,=\,t\vec{u}$ , autrement dit tel que :

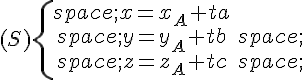
$(S)\{\begin{matrix}\,x=x_A+ta\\\,y=y_A+tb\,\\\,z=z_A+tc\,\end{matrix}.$

Définition :

Le système (S) est une représentation paramétrique de la droite (d).
t est le paramètre de cette représentation.

Exemple :

(d) est la droite qui passe par le point $A(2\,;\,-\,3\,;\,1)$ et de vecteur directeur $\vec{u}(3\,;\,4\,;\,2)$ ;
Une représentation paramétrique de d est

2. Utiliser une représentation paramétrique.

Définition :

Une droite (d) admet une infinité de représentations paramétriques.En effet, on peut choisir un point de (d) autre que A ou choisir un vecteur non nul colinéaire à $\vec{u}$ et autre que $\vec{u}$ .

Exemple :

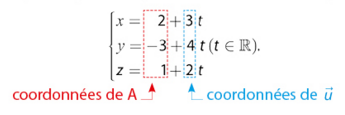
On reprend l’exemple du paragraphe 1 .
• Le point $B(5\,;\,1\,;\,3)$ (obtenu pour $t\,=\,1$ ) appartient à (d), donc une autre représentation paramétrique de (d) est :

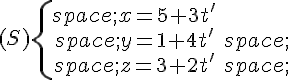
$(S)\{\begin{matrix}\,x=5+3t'\\\,y=1+4t'\,\\\,z=3+2t'\,\end{matrix}.$ $(t'\,\in\mathbb{R}\,)$ .

• Le vecteur $\vec{v}(-6\,;\,-\,8\,;\,-\,4)$ est un autre vecteur directeur de (d), donc une autre représentation paramétrique de (d) est :

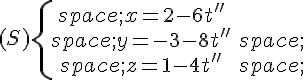
$(S)\{\begin{matrix}\,x=2-6t''\\\,y=-3-8t''\,\\\,z=1-4t''\,\end{matrix}.$ $(t''\,\in\mathbb{R}\,)$ .

Remarque :

Par un raisonnement analogue à celui du paragraphe 1, on obtient une représentation paramétrique d’un plan à partir d’un de ses points et d’un couple de vecteurs non colinéaires de ce plan.

II. Équations cartésiennes d’un plan.

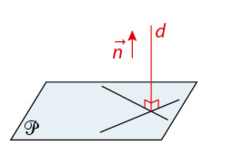
1. Vecteur normal à un plan.

Définition :

Dire qu’un vecteur non nul $\vec{n}$ est normal à un plan

signifie que
toute droite de vecteur directeur $\vec{n}$ est orthogonale au plan

Propriété :

A est un point de l’espace et $\vec{n}$ est un vecteur non nul.
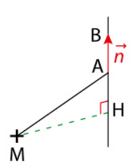
L’ensemble des points M de l’espace tels que $\vec{AM}.\vec{n}=0$ est le plan

passant par A et de vecteur normal $\vec{n}$ .

Preuve :

On note B le point distinct de A tel que $\vec{n}=\vec{AB}$ et H le projeté orthogonal d’un point M sur la droite (AB).

Avec ces notations :

$\vec{AM}.\vec{n}=\,\vec{AM}.\vec{AB}=\vec{AH}.\vec{AB}.$

Ainsi $\vec{AM}.\vec{n}=0$ si, et seulement si, $\vec{AH}.\,\vec{AB\,}=\,0$ , c’est-à-dire A = H car les vecteurs $\vec{AH}$

et $\vec{AB}$ sont colinéaires.

Autrement dit, $\vec{AM}.\vec{n}=0$ si, et seulement si, A est le projeté orthogonal de M sur la droite (AB).
L’ensemble cherché est donc le plan passant par A et orthogonal à (AB).

2. Équations cartésiennes d’un plan.

Propriétés et définition :

L’espace est muni d’un repère orthonormé.
1. Un plan de vecteur normal $\vec{n}(a\,;\,b\,;\,c)$ a une équation de la forme $ax+\,by\,+\,cz\,+\,d\,=0$ , où d désigne
un nombre réel.On dit que c’est une équation cartésienne de ce plan.
2. Réciproquement, a, b, c et d étant quatre nombres réels donnés avec a, b et c non tous nuls, l’ensemble des points $M(x\,;\,y\,;\,z)$ tels que $ax+\,by\,+\,cz\,+\,d\,=0$ est un plan de vecteur normal $\vec{n}(a\,;\,b\,;\,c)$ .

Preuve :

1. Un point $M(x\,;\,y\,;\,z)$ appartient au plan passant par $A(x_A\,;\,y_A\,;\,z_A)$ et de

vecteur normal $\vec{n}$ si, et seulement si, $\vec{AM}.\vec{n}=0$ , c’est-à-dire ;

En posant $d\,=\,-(ax_A\,+\,by_A\,+\,cz_A)$ , on obtient $ax\,+\,by\,+\,cz\,+\,d\,=\,0$ .

2. $(\varphi\,)$ est l’ensemble des points $M(x\,;\,y\,;\,z)$ qui vérifie $ax+\,by\,+\,cz\,+\,d\,=0$

où a, b et c sont des nombres réels non tous nuls.

On peut supposer, par exemple, $a\neq\,0$ .

Le point $A(-\frac{d}{a};0;0)$ est alors un point de $(\varphi\,)$ et l’équation équivaut à $a(x+\frac{d}{a})+by+cz=0$ ,

c’est-à-dire

$\vec{AM}.\vec{n}=0$ avec $\vec{n}(a\,;\,b\,;\,c)$ .

$(\varphi\,)$ est donc le plan passant par A et de vecteur normal $\vec{n}(a\,;\,b\,;\,c)$ .

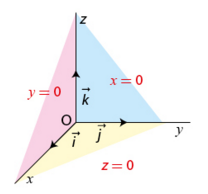
3. Cas particuliers des plans (xOy), (yOz) et (xOz).

• Le plan passe par l’origine $O(0\,;\,0\,;\,0)$ du repère et le vecteur $\vec{k}(0;\,0\,;\,1)$ est un vecteur normal à ce plan.
Ainsi, une équation cartésienne du plan est de la forme $0x\,+\,0y\,+\,1z\,+\,d=0$ .
Or, $O(0\,;\,0\,;\,0)$ appartient à donc $1\,\times \,0+\,d\,=\,0$ et $d\,=\,0$ .
Ainsi, une équation cartésienne du plan est $z\,=\,0$ .

• De même, le plan a pour équation cartésienne et le plan a pour équation cartésienne .

III. Traduire un problème par un système d’équations linéaires.

1. Déterminer l’intersection de deux droites.

Exemple :

Dans un repère orthonormé, on se propose de démontrer que les droites (d) et (d’) de représentations paramétriques respectives :

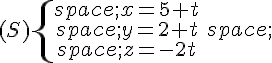
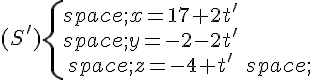
$(S)\{\begin{matrix}\,x=5+t\\\,y=2+t\,\\\,z=-2t\end{matrix}.$ $(t\,\in\mathbb{R}\,)$ et $(S')\{\begin{matrix}\,x=17+2t'\\\,y=-2-2t'\\\,z=-4+t'\,\end{matrix}.$ $(t'\,\in\mathbb{R}\,)$ sont sécantes.

Les droites (d) et (d’) sont sécantes si, et seulement si, le système ci-dessous de six équations
à cinq inconnues $t,\,t',\,x,\,y,\,z$ a une seule solution.

$\{\begin{matrix}\,x=5+t\\\,y=2+t\,\\\,z=-2t\\x=17+2t'\\\,y=-2-2t'\\\,z=-4+t'\end{matrix}.$

Autrement dit, (d) et (d’) sont sécantes si, et seulement si, il existe un unique couple $(t\,;\,t')$ tel que :

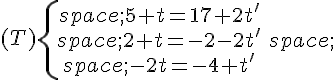
$(T)\{\begin{matrix}\,5+t=17+2t'\\\,2+t=-2-2t'\,\\\,-2t=-4+t'\end{matrix}.$ c’est-à-dire $\{\begin{matrix}\,t-2t'=12\,\,\,(1)\\\,t+2t'=-4\,\,\,(2)\\\,-2t-t'=-4\,\,(3)\end{matrix}.$

Pour résoudre ce système (T) de trois équations à deux inconnues, on commence par résoudre un système formé par deux de ces équations, par exemple (1) et (2) comme ci-dessous.

Ce système ayant un seul couple solution, on vérifie qu’il est aussi solution de (3).
On conclut que ce couple est solution de (T).

• Par addition membre à membre des équations (1) et (2), on obtient $2t=\,8$ soit $t\,=4$ .
• On remplace t par 4 dans l’équation (1), on obtient $4\,-\,2t'=\,12$
soit $t'\,=-4$ .
• On vérifie que les valeurs de t et t’ obtenues sont solutions de l’équation (3) :

$-2\times \,4-(-4)=-4$ .

• On remplace t par 4 dans le système (S) ou par dans et on obtient les coordonnées du point d’intersection de (d) et (d’) : .

Remarque :

Il est important de noter l’utilité d’avoir nommé différemment les paramètres t et t’. En effet, le
point commun M à (d) et (d’) est atteint sur (d) pour $t=\,4$ , alors qu’il est atteint sur (d’) pour $t'\,=-4$ .

2. Étudier l’intersection d’une droite et d’un plan.

Exemple :

Dans un repère orthonormé, le plan a pour équation cartésienne $5x\,+\,y\,-z+3=0$
et la droite pour représentation paramétrique :

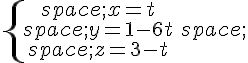
$\{\begin{matrix}\,x=t\\\,y=1-6t\,\\\,z=3-t\end{matrix}.$ $(t\,\in\mathbb{R}\,)$

On se propose d’étudier l’intersection du plan et de la droite .
Pour cela, on résout le système ci-dessous de quatre équations à quatre inconnues $x,\,y,\,z,\,t$ .

$(S)\{\begin{matrix}\,x=t\\\,y=1-6t\,\\\,z=3-t\\\,5x+y-z+3=0\end{matrix}.$

Ce système équivaut à :

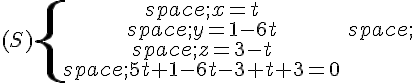
$(S)\{\begin{matrix}\,x=t\\\,y=1-6t\,\\\,z=3-t\\\,5t+1-6t-3+t+3=0\end{matrix}.$ c’est-à-dire $(S)\{\begin{matrix}\,x=t\\\,y=1-6t\,\\\,z=3-t\\\,0t=-1\end{matrix}.$

Or, la quatrième équation n’a pas de solution donc le système (S) n’a pas de solution.

La droite (d) et le plan n’ont pas de point commun, donc (d) est strictement parallèle à .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «représentation paramétrique et équation cartésienne : cours de maths en terminale en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.