Continuité : exercices corrigés de maths en terminale en PDF.

La continuité et théorème des valeurs intermédiaires à travers des exercices de maths en terminale corrigés. Vous pouvez travailler sur les énoncés à difficultés variables et également, consulter leur correction détaillée.

Exercice 1 – Etude d’une fonction f

Soit f la fonction définie sur $[0;+\infty[$ par $f(x)=5-\frac{8}{x+2}$ .

1. Etudier les variations de f sur $[0;+\infty[$ .

2. Résoudre l’équation sur l’intervalle $[0;+\infty[$ .

On note $\alpha$ cette solution .

Exercice 2 – Fonction continue qui ne s’annule jamais

Montrer qu’une fonction continue sur R qui ne s’annule jamais est de signe constant.

Exercice 3 – Tangente et unicité d’une solution

Montrer que l’équation tan x = x possède une unique solution dans $]\frac{\pi}{2};\frac{3\pi}{2}[.$

Exercice 4 – Continuité et théorème du point fixe

Montrer que toute application continue d’un segment dans lui-même admet un point ﬁxe :

Exercice 5 – Montrer qu’il y a une unique racine
Soit f la fonction définie sur $\mathbb{R}^+$ par $f(x)=x^2+\sqrt{x}-3.$
Montrer que f possède une unique racine puis en donner un encadrement d’amplitude 0, 01.
Exercice 6 – Etude d’un polynôme
. Soit P la fonction définie sur $\mathbb{R}$ par
1. Dresser le tableau de variations de P.

2. En déduire le nombre de racines de P.
3. Retrouver directement ces racines en factorisant P(x).

Exercice 7 – Théorème des valeurs intermédiaires

Montrer que tout polynôme de degré impair possède au moins une racine réelle.

Exercice 8 – Racine et théorème des valeurs intermédiaires

Soit f la fonction définie sur R par

Montrer que f possède une unique racine.

Exercice 9 :

La fonction de Heaviside, notée H, du nom d’un physicien anglais (1850-1925) est couramment
utilisée en automatisme.
Pour tout réel x, $H(x)=\{\begin{matrix}\,0\,si\,x<0\\\,1\,si\,x\,\geq\,\,0\,\end{matrix}.$
a) Dans un repère, tracer la courbe représentative de la fonction H.
b) Sur quels intervalles, les plus grands possibles, la fonction H est-elle continue ?

Exercice 10 :

La partie entière d’un nombre réel x, notée E(x), est l’unique entier relatif n tel que :

$n\leq\,\,x<n+1$
1.Déterminer :

$a.\,E(2,6)\,b.\,E(0,3)\,c.\,E(4)\,d.\,E(-1,2)$
2.Déterminer E(x) pour tout réel de l’intervalle :
$a)[0;1[\,b)[1;2[\,c)[-1;0[\,d)[-2;-1[$

3.a) Dans un repère, tracer la courbe représentative de la fonction E sur l’intervalle [-5;5[ .
b) Étudier graphiquement la continuité de la fonction E sur l’intervalle [-5;5[ .
c) De façon plus générale, en quels nombres réels la fonction E est-elle discontinue ?

Exercice 11 :

f est la fonction définie sur $\mathbb{R}$ par :

$f(x)=\{\begin{matrix}\,1-2x\,si\,x\,\geq\,\,2\\\,e^{x-2}-4\,si\,x\,<\,2\,\end{matrix}.$

a. Expliquer pourquoi la fonction f est continue sur l’intervalle $]2\,;\,+\,\infty[$ , puis sur l’intervalle $]-\,\infty\,;\,2[$ .
b. Expliquer pourquoi :

$\lim_{\,x\to\,2^+}\,f(x)=-3$ et $\lim_{\,x\to\,2^-}\,f(x)=-3$

Que peut-on en déduire pour la fonction f ?
c) Conclure pour la continuité de la fonction f sur $\mathbb{R}$ .

Exercice 12 :

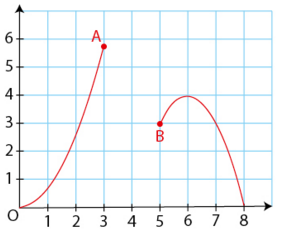
Un designer a dessiné une partie d’un logo dans le repère ci-dessous.

Ce logo est la courbe représentative de la fonction f définie sur l’intervalle [0 ; 8] par :
$f(x)=\{\begin{matrix}\,1-2x\,si\,x\,\geq\,\,2\\\,e^{x-2}-4\,si\,x\,<\,2\,\end{matrix}.$ $f(x)=\{\begin{matrix}\,0,64x^2\,si\,0\leq\,\,x\leq\,\,3\,\\\,ax+b\,si\,3<x\,<\,5\\4-(x-6)^2\,\,si\,\,5\leq\,\,x\leq\,\,8\,\end{matrix}.$
a) Déterminer les nombres réels a et b afin que la fonction f soit continue sur l’intervalle [0 ; 8].
b) Déterminer le nombre dérivé en 3 de la fonction polynôme $x\,\mapsto \,0,64x^2$ , puis de la fonction affine
$x\,\mapsto \,1,38x\,+\,9,9$ .
La fonction f est-elle dérivable en 3 ?
c) Étudier la dérivabilité de la fonction f en 5.

Exercice 13 :

(v_n) est la suite définie pour tout entier naturel $n\,\geq\,\,2$ par $v_n=\sqrt{\frac{n+1}{n-1}}$ .
a) Proposer une suite (u_n) et une fonction f telles que pour tout entier naturel $n\,\geq\,\,2$ , .
b) Démontrer que la suite (v_n) est convergente et préciser sa limite.

Exercice 14 :

f est la fonction définie sur I=[1 ; 2] par :
$f(x)=5-\frac{16}{3+x}$
a) Étudier le sens de variation de la fonction f sur l’intervalle I et dresser son tableau de variations.
b) Vérifier que pour tout réel x de I, $f(x)\,\in\,I$ .
2. (u_n) est la suite définie par u_0=2 et pour tout entier naturel n, $u_{n+1}=f(un).$
a) Démontrer par récurrence que la suite (u_n) :
• est décroissante ;
• est minorée par 1.
b) En déduire que la suite (u_n) converge vers un réel .
c) Expliquer pourquoi est solution dans I de l’équation $f(x)\,=\,x$ .

Déterminer .

Exercice 15 :

f est la fonction définie sur $\mathbb{R}$ par :
$f(x)=\,3x^4\,-\,8x^3\,-\,6x^2\,+\,24x$ .
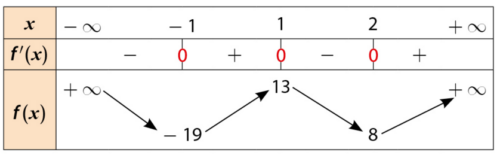
Voici le tableau de variations de la fonction f.

a) Démontrer que l’équation f(x) = 0 admet deux solutions $\alpha$ et $\beta$ dans $\mathbb{R}$ avec $\alpha\,<\beta$ .
b) Donner la valeur exacte de $\beta$ et un encadrement d’amplitude $10^{-2}$ de $\alpha$ à l’aide de la calculatrice.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «continuité et théorème des valeurs intermédiaires : exercices de maths en terminale corrigés en PDF.» au format PDF.

D'autres cours et exercices à consulter

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.