Amérique du Nord : bac de maths 2024 sujet 2 corrigé en PDF.

Amérique du Nord : bac de maths 2024 sujet 2 corrigé en PDF. Ce sujet porte sur les probabilités, l’étude d’un pavé droit et des équations cartésiennes de plans. Des fonctions et suites numériques avec un programme réalisé avec Python. L’étude d’une fonction logarithme et des tangentes à sa courbe.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
Amérique du Nord – SESSION 2024
MATHÉMATIQUES
Jour 2
Durée de l’épreuve : 4 heures

L ‘usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire « type collège » est autorisé.

Exercice 1 : (5 points)
Les données publiées le 1er mars 2023 par le ministère de la transition écologique sur les
immatriculations de véhicules particuliers en France en 2022 contiennent les informations
suivantes :
• 22,86 % des véhicules étaient des véhicules neufs ;
• 8,08 % des véhicules neufs étaient des hybrides rechargeables ,
• 1,27 % des véhicules d’occasion (c’est-à-dire qui ne sont pas neufs) étaient des hybrides rechargeables.
Dans tout l’exercice, les probabilités seront arrondies au dix-millième.

Partie A
Dans cette partie, on considère un véhicule particulier immatriculé en France en 2022.
On note
• N l’événement « le véhicule est neuf » ;
• R l’événement « le véhicule est hybride rechargeable » ;
• $\overline{N}$ et $\overline{R}$ les événements contraires des événements contraires de N et R.

1. Représenter la situation par un arbre pondéré.
2. Calculer la probabilité que ce véhicule soit neuf et hybride rechargeable.
3. Démontrer que la valeur arrondie au dix-millième de la probabilité que ce véhicule
soit hybride rechargeable est 0,0283.

4. Calculer la probabilité que ce véhicule soit neuf sachant qu’il est hybride rechargeable.

Partie B
Dans cette partie, on choisit 500 véhicules particuliers hybrides rechargeables immatriculés
en France en 2022.

Dans la suite, on admettra que la probabilité qu’un tel véhicule soit neuf est égale à 0,65.
On assimile le choix de ces 500 véhicules à un tirage aléatoire avec remise.
On appelle X la variable aléatoire représentant le nombre de véhicules neufs parmi les 500
véhicules choisis.
1. On admet que la variable aléatoire X suit une loi binomiale. Préciser la valeur de ses
paramètres.

2. Déterminer la probabilité qu’exactement 325 de ces véhicules soient neufs.
3. Déterminer la probabilité $p(X\geq\,\,325)$ puis interpréter le résultat dans le contexte de
l’exercice.

Partie C
On choisit désormais n véhicules particuliers hybrides rechargeables immatriculés en
France en 2022, où n désigne un entier naturel strictement positif.
On rappelle que la probabilité qu’un tel véhicule soit neuf est égale à 0,65.
On assimile le choix de ces n véhicules à un tirage aléatoire avec remise.
1. Donner l’expression en fonction de n de la probabilité que tous ces véhicules
soient d’occasion.

2. On note la probabilité qu’au moins un de ces véhicules soit neuf.

En résolvant une inéquation, déterminer la plus petite valeur de n telle que $q_n\,\geq\,\,0,9999$ .

Exercice 2 : (5 points)
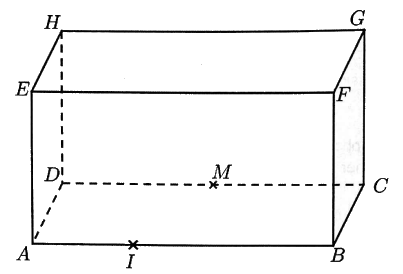
On considère le pavé droit ABCDEFGH tel que AB = 3 et AD = AE = 1 représenté ci-dessous.

On considère le point I du segment [AB] tel que $\vec{AB}\,=\,3\vec{AI}$ et on appelle M le milieu du
segment [CDI.
On se place dans le repère orthonormé $(A;\vec{AI},\vec{AD},\vec{AE})$ .
1. Sans justifier, donner les coordonnées des points F, H et M.

2.a) Montrer que le vecteur 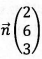est un vecteur normal au plan (HMF).
b) En déduire qu’une équation cartésienne du plan (HMF) est :
$2x+\,6y\,+\,3z-9=0$ .

c) Le plan dont une équation cartésienne est $5x\,+\,15y\,-\,3z+\,7\,=\,0$ est-il parallèle au plan (HMF) ? Justifier la réponse.
3. Déterminer une représentation paramétrique de la droite (DG).
4. On appelle N le point d’intersection de la droite (DG) avec le plan (HMF).
Déterminer les coordonnées du point N.
5. le point R de coordonnées $(3;\frac{1}{4};\frac{1}{2})$ est-il le projeté orthogonal du point G sur le plan
(HMF)? Justifier la réponse.

Exercice 3 : (6 points)
On considère la fonction g définie sur l’intervalle [0; 1] par $g(x)\,=\,2x\,-x^2$ .
1. Montrer que la fonction g est strictement croissante sur l’intervalle [0; 1] et préciser
les valeurs de g(0) et de g(l).

On considère la suite définie par

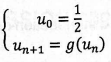
pour tout entier naturel n.
2. Calculer et .
3. Démontrer par récurrence que, pour tout entier naturel n, on a : $0\,<\,u_n\,<\,u_{n\,+1}\,<\,1$ .
4. En déduire que la suite est convergente.
5. Déterminer la limite de la suite .

On considère la suite définie pour tout entier naturel n par $v_n\,=\,ln(1\,-u_n)$ .
6. Démontrer que la suite est une suite géométrique de raison 2 et préciser son premier terme.
7. En déduire une expression de en fonction de n.
8. En déduire une expression de en fonction de n et retrouver la limite déterminée à
la question 5.
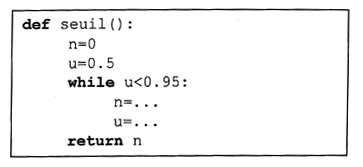
9. Recopier et compléter le script Python ci-dessous afin que celui-ci renvoie le rang n
à partir duquel la suite dépasse 0,95.

Exercice 4 : (4 points)
Soit un réel strictement positif.
On considère la fonction définie sur l’intervalle $]0\,;\,+\infty[$ par $f(x)\,=\,a\,ln(x)$ .
On note sa courbe représentative dans un repère orthonormé.
Soit un réel strictement supérieur à 1.
1. Déterminer l’abscisse du point d’intersection de la courbe et de l’axe des abscisses.
2. Vérifier que la fonction F définie par $F(x)\,=\,a(xln(x)\,-x)$ est une primitive de la
fonction f sur l’intervalle $]0\,;\,+\infty[$ .
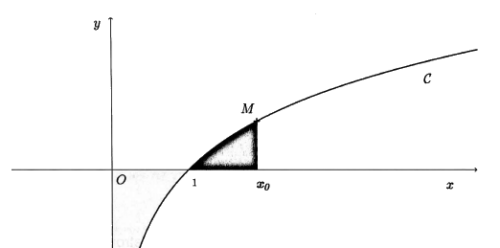
3. En déduire l’aire du domaine grisé en fonction de et de .

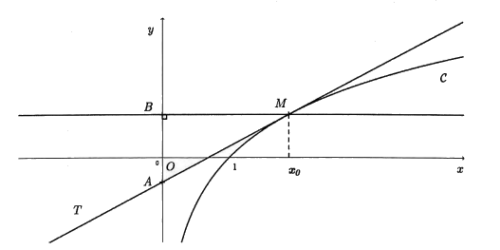
On note T la tangente à la courbe au point M d’abscisse .
On appelle A le point d’intersection de la tangente T avec l’axe des ordonnées et B le projeté
orthogonal de M sur l’axe des ordonnées.

4. Démontrer que la longueur AB est égale à une constante (c’est-à-dire à un nombre
qui ne dépend pas de ) que l’on déterminera.

Le candidat prendra soin d’expliciter sa démarche.

Consulter le corrigé

5/5 - (11 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «amérique du Nord : bac de maths 2024 sujet 2 corrigé en PDF.» au format PDF.

D'autres fiches similaires :

Mathovore c'est 13 980 191 cours et exercices de maths téléchargés en PDF.