Suites numériques : cours de maths en terminale en PDF.

Les suites numériques dans un cours de maths en terminale en enseignement obligatoire.

Nous étudierons la définition d’une suite numérique et son comportement.

I . Comportement d’une suite numérique :

Définition :

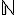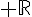Une suite est une application de l’ensemble $\mathbb{N}$ dans l’ensemble $\mathbb{R}$ .

$\begin{array}{l|rcl} (U_n): \mathbb{N} \longrightarrow \mathbb{N} \\ n \longrightarrow U_n \end{array}$ .

Définitions :

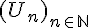Une suite $(U_n)_{n\in\mathbb{N}$ est croissante $\Leftrightarrow\,\,\forall n \in \mathbb{N},\,U_n \le U_{n+1}$ .
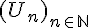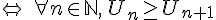Une suite $(U_n)_{n\in\mathbb{N}$ est décroissante $\Leftrightarrow\,\,\forall n \in \mathbb{N},\,U_n \ge U_{n+1}$ .
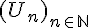Une suite $(U_n)_{n\in\mathbb{N}$ est monotone signifie qu’elle est soit croissante soit décroissante.

Remarques :

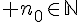
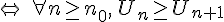
On parle aussi de suite $(U_n)_{n\in\mathbb{N}$ croissante à partir d’un rang $n_0\in\mathbb{N}$ $\Leftrightarrow\,\,\forall n \ge n_0,\,U_n \ge U_{n+1}$
On définit aussi les suites strictement croissantes ou décroissante en remplaçant les inégalités par des inégalités strictes .

Méthode 1 :

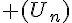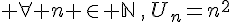
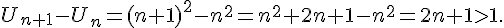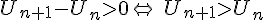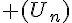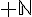Considérons la suite définie par $\forall n \in \mathbb{N}\,,\,U_n=n^2$ $U_{n+1}-U_n={(n+1)}^2-n^2=n^2+2n+1-n^2=2n+1>1 .$ (car n est un entier naturel donc positif) donc $U_{n+1}-U_n>0\Leftrightarrow\,\,U_{n+1}>U_n$ donc la suite est strictement croissante sur $\mathbb{N}$ .

Méthode 2 :

Pour une suite 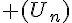à termes strictement positifs : comparer 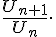$\frac{U_{n+1}}{U_n} .$ et 1.

Considérons la suite 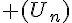définie par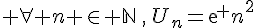 $\forall n \in \mathbb{N}\,,\,U_n={exp n}^2$

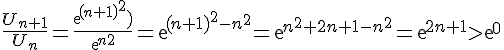$\frac{U_{n+1}}{U_n}= \frac{exp (n+1)^2)}{exp n^2}=exp {(n+1)^2-n^2}=exp{n^2+2n+1-n^2}=exp{2n+1} > exp 0$ car la fonction exp est strictement croissante sur 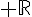$\mathbb{R}$ et 2n+1 >0 .

donc 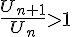$\frac{U_{n+1}}{U_n}>1$ car

ainsi 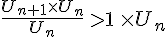$\frac{U_{n+1}\times U_n}{U_n}\,>1\,\times U_n$

car 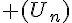est à termes strictement positifs .

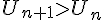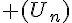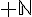$U_{n+1}> U_n$ donc est strictement croissante sur $\mathbb{N}$ .

Définitions :

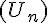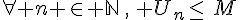Une suite est majorée lorsqu’il existe un réel M (un majorant) tel que $\forall n \in \mathbb{N}\,,\, U_n\le\,M$ .
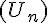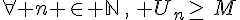Une suite est minorée lorsqu’il existe un réel m tel que $\forall n \in \mathbb{N}\,,\, U_n\ge\,M$ .
Une suite 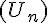est bornée lorsqu’elle est majorée et minorée .

Remarques :

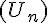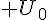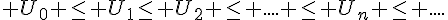
Si est une suite croissante, alors elle est minorée par son premier terme : $U_0 \le U_1\le U_2 \le .... \le U_n \le ....$
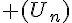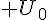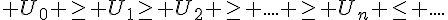
Si est une suite décroissante, alors elle est majorée par son premier terme : $U_0 \ge U_1\ge U_2 \ge .... \ge U_n \le ....$

Exemples :

La suite 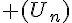définie par 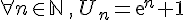$\forall n \in \mathbb{N}\,,\, U_n = exp n + 1$ est strictement croissante, elle est minorée par 1 par contre, elle n’est pas majorée.
La suite 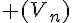définie par 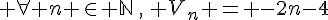$\forall n \in \mathbb{N}\,,\, V_n = -2n-4$ est strictement décroissante, majorée par -4, par contre elle n’est pas minorée .
La suite 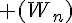définie par 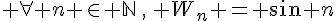$\forall n \in \mathbb{N}\,,\, W_n = sin n$ est bornée, majorée par 1 et minorée par -1.

Théorème :

Une suite croissante et majorée est convergente .
Une suite décroissante et minorée est convergente .

Théorème :

Toute suite croissante non majorée, diverge vers $+\infty$ .
Tout suite décroissante non minorée diverge vers $-\infty$ .

Exemple :

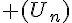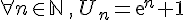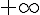La suite définie par $\forall n \in \mathbb{N}\,,\, U_n = exp n + 1$ est strictement croissante, elle n’est pas majorée donc diverge vers $+\infty$ .
La suite 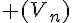définie par 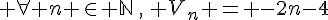$\forall n \in \mathbb{N}\,,\, V_n = -2n-4$ est strictement décroissante, elle n’est pas minorée donc diverge vers $-\infty$ .
La suite 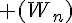définie par 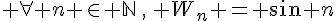$\forall n \in \mathbb{N}\,,\, W_n = sin n$ est bornée, elle est dite divergente .

Théorème :

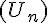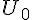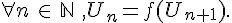Soit (U_n) définie par U_0 et $\forall n \,\in\, \mathbb{N}\,\,, U_n=f(U_{n+1}) .$ .

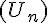Si (U_n) converge vers 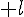et si f est continue en 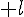alors cette limite 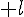vérifie $f(l)\,=\,l$ .

Exemple :

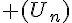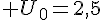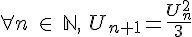Considérons définie par et $\forall n\,\, \in\,\, \mathbb{N},\,\, U_{n+1}=\frac{U_n^2}{3}$ .

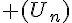est décroissante et minorée par 0 ( à montrer…).

Donc 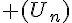converge vers 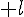d’après le théorème précédent .

Posons 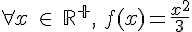$\forall x\,\, \in\,\, \mathbb{R^+},\,\, f(x)=\frac{x^2}{3}$

On est amené à résoudre 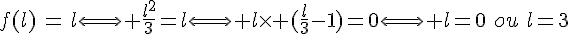$f(l)\,=\,l\Longleftrightarrow \frac{l^2}{3}=l\Longleftrightarrow l\times (\frac{l}{3}-1)=0\Longleftrightarrow l=0\,\,ou\,\,l=3$

$\forall n\,\, \in\,\, \mathbb{N},\,\, U_n\le 2,5$

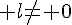
donc $l\neq 0$

d’où

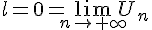
$l= 0=\lim_{n\to +\infty} U_n$

II . Suites adjacentes :

Définition :

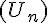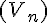Dire que deux suites (U_n) et (V_n) sont adjacentes signifie que :

L’une est croissante.
L’autre est décroissante.
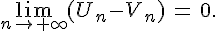
$\lim_{n \to +\infty} (U_n-V_n)\,=\,0.$

Exemple :

Considérons les deux suites numériques suivantes :

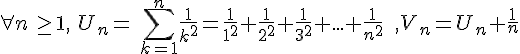
$\forall n\,\ge 1,\,\, U_n=\,\sum_{k=1}^{n}\frac{1}{k^2}= \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{n^2}\,\,\,\,,V_n=U_n+\frac{1}{n}$

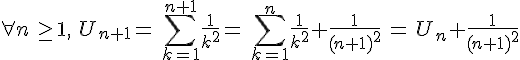$\forall n\, \ge 1,\,\, U_{n+1}=\,\sum_{k=1}^{n+1}\frac{1}{k^2}= \,\sum_{k=1}^{n}\frac{1}{k^2}+\frac{1}{(n+1)^2}\,=\,U_n+\frac{1}{(n+1)^2}$ .

Donc $U_{n+1}-U_n\,=\,\frac{1}{{n+1}^2}>0$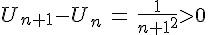

donc 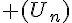est croissante .

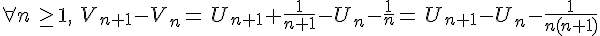$\forall n\, \ge 1,\,\, V_{n+1}-V_n=\,U_{n+1}+\frac{1}{n+1}-U_n-\frac{1}{n}= \,U_{n+1}-U_n-\frac{1}{n(n+1)}$ .

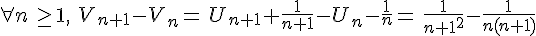
$\forall n\, \ge 1,\,\, V_{n+1}-V_n=\,U_{n+1}+\frac{1}{n+1}-U_n-\frac{1}{n}=\,\frac{1}{{n+1}^2}-\frac{1}{n(n+1)}$

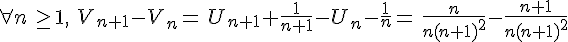
$\forall n\, \ge 1,\,\, V_{n+1}-V_n=\,U_{n+1}+\frac{1}{n+1}-U_n-\frac{1}{n}=\,\frac{n}{n(n+1)^2}-\frac{n+1}{n(n+1)^2}$

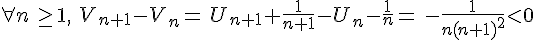
$\forall n\, \ge 1,\,\, V_{n+1}-V_n=\,U_{n+1}+\frac{1}{n+1}-U_n-\frac{1}{n}=\,-\frac{1}{n(n+1)^2}<0$

donc 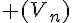est décroissante .
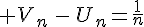
$V_n\,-\,U_n=\frac{1}{n}$
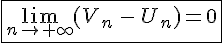
$\fbox{ \lim_{n\to +\infty} ( V_n\,-\,U_n)=0}$

Conclusion :

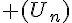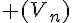Les deux suites et sont adjacentes .

Définition :

Si deux suites sont adjacentes alors elles convergent vers la même limite.

Exemple :

Reprenons notre exemple précédente :

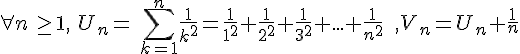
$\forall n\,\ge 1,\,\, U_n=\,\sum_{k=1}^{n}\frac{1}{k^2}= \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{n^2}\,\,\,\,,V_n=U_n+\frac{1}{n}$

Les deux suites 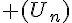et 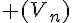sont adjacentes donc elles sont convergentes et convergent vers la même limite .

Nous pourrions montrer que :
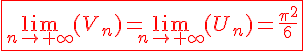
$\fbox{ \lim_{n\to +\infty} ( V_n\)=\lim_{n\to +\infty} (U_n)=\frac{\pi^2}{6}$

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les suites numériques : cours de maths en terminale en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.