Asie Pacifique bac de maths 2024 : sujet n° 2 corrigé

Le bac de maths 2024 en Asie Pacifique sujet n° 2. Ce sujet dispose de son corrigé afin que les élèves de maths révisent leur baccalauréat en ligne. Ce sujet porte sur l’étude d’une fonction contenant un logarithme et sa dérivée seconde, l’étude des variations d’une fonction auxiliaire et la limite d’une suite récurrente. Des probabilités sur les victoires à un jeu vidéo ainsi que la suite correspondante et un programme réalisé en Python. Des affirmations vraie ou fausse à démontrer. L’équation d’un plan avec l’équation paramétrique d’une droite avec la norme d’un vecteur et le calcul de l’aire d’un triangle.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
ASIE PACIFIQUE -SESSION 2024
MATHÉMATIQUES
Sujet n° 2
Durée de l’épreuve : 4 heures
Coefficient : 16

L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire, « type collège » est autorisé.

Le sujet est composé de 4 exercices indépendants.
Tous les exercices doivent être traités.
La qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l’appréciation des copies.
Les candidates et les candidats sont invités à faire figurer sur leurs copies toute trace de recherche, même incomplète ou infructueuse.

Exercice 1 : (5,5 points)

On considère la fonction définie sur $]0;+\infty[$ par .
On admet que est deux fois dérivable sur $]0;+\infty[$ .
On note la fonction dérivée de la fonction et la fonction dérivée de la fonction .

Partie A : Étude de la fonction f
1. Déterminer les limites de la fonction en 0 et en $+\infty$ .
2. Pour tout réel strictement positif, calculer .
3. Montrer que pour tout réel strictement positif :

$f''(x)=\frac{2x-1}{x}$

4. Étudier les variations de la fonction sur $]0;+\infty[$ , puis dresser le tableau des
variations de la fonction sur $]0;+\infty[$ .
On veillera à faire apparaître la valeur exacte de l’extremum de la fonction sur $]0;+\infty[$ .
Les limites de la fonction aux bornes de l’intervalle de définition ne sont pas attendues.
5. Montrer que la fonction est strictement croissante sur $]0;+\infty[$ .

Partie B : Étude d’une fonction auxiliaire pour la résolution de l’équation f(x) =x.
On considère dans cette partie la fonction définie sur $]0;+\infty[$ par $g(x)\,=\,x-ln\,(x)$ .
On admet que la fonction est dérivable sur $]0;+\infty[$ , on note sa dérivée.
1. Pour tout réel strictement positif, calculer , puis dresser le tableau des variations de
la fonction .

Les limites de la fonction aux bornes de l’intervalle de définition ne sont pas attendues.
2. On admet que 1 est l’unique solution de l’équation .
Résoudre, sur l’intervalle $]0;+\infty[$ , l’équation .

Partie C : Étude d’une suite récurrente
On considère la suite définie par $u_0=\frac{1}{2}$ et pour tout entier naturel ,
$u_{n+1}=f(u_n)=u_n^2-u_nln(u_n)$ .

1. Montrer par récurrence que pour tout entier naturel ,

$\frac{1}{2}\leq\,\,u_n\leq\,\,u_{n+1}\leq\,\,1$ .

2. Justifier que la suite converge.
On appelle la limite de la suite et on admet que vérifie l’égalité .
3. Déterminer la valeur de .

Exercice 2 : (5,5 points)
Léa passe une bonne partie de ses journées à jouer à un jeu vidéo et s’intéresse aux
chances de victoire de ses prochaines parties.
Elle estime que si elle vient de gagner une partie, elle gagne la suivante dans 70% des cas.
Mais si elle vient de subir une défaite, d’après elle, la probabilité qu’elle gagne la suivante
est de 0,2.
De plus, elle pense avoir autant de chance de gagner la première partie que de la perdre.

On s’appuiera sur les affirmations de Léa pour répondre aux questions de cet exercice.

Pour tout entier naturel non nul, on définit les événements suivants :
• : « Léa gagne la -ième partie de la journée » ;
• : « Léa perd la -ième partie de la journée ».

Pour tout entier naturel non nul, on note la probabilité de l’événement .
On a donc $g_1\,=\,0,5$ .
1. Quelle est la valeur de la probabilité conditionnelle $P_{G_1}(D_2)$ ?
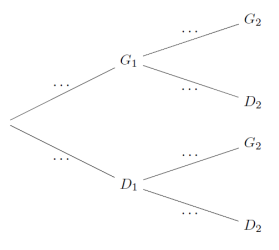
2. Recopier et compléter l’arbre des probabilités ci-dessous qui modélise la situation pour
les deux premières parties de la journée :

3. Calculer .

4. Soit un entier naturel non nul.
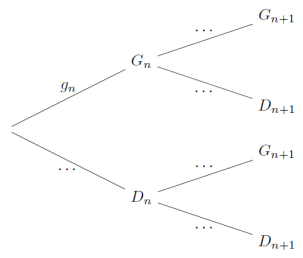
a. Recopier et compléter l’arbre des probabilités ci-dessous qui modélise la situation pour
les -ième et ( + 1)-ième parties de la journée.
b. Justifier que pour tout entier naturel non nul, $g_{n+1}=\,0,5g_n\,+\,0,2$ .

5. Pour tout entier naturel non nul, on pose $v_n=\,g_n-\,0,4$ .
a. Montrer que la suite est géométrique. On précisera son premier terme et sa raison.
b. Montrer que, pour tout entier naturel non nul : $g_n=0,1\times \,0,5^{n-1}+0,4$ .
6. Étudier les variations de la suite .
7. Donner, en justifiant, la limite de la suite .
Interpréter le résultat dans le contexte de l’énoncé.

8. Déterminer, par le calcul, le plus petit entier tel que $g_n-\,0,4\,\leq\,\,0,001$ .

9. Recopier et compléter les lignes 4, 5 et 6 de la fonction suivante, écrite en langage
Python, afin qu’elle renvoie le plus petit rang à partir duquel les termes de la suite sont
tous inférieurs ou égaux à $0,4\,+e$ , où est un nombre réel strictement positif.

Exercice 3 : (4 points)
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.

1. Soit une suite définie pour tout entier naturel et vérifiant la relation suivante :
pour tout entier naturel , $\frac{1}{2}<u_n\,\leq\,\,\frac{3n^2+4n+7}{6n^2+1}$ .
Affirmation 1 :

$\lim_{n\to\,+\infty}u_n=\frac{1}{2}$ .

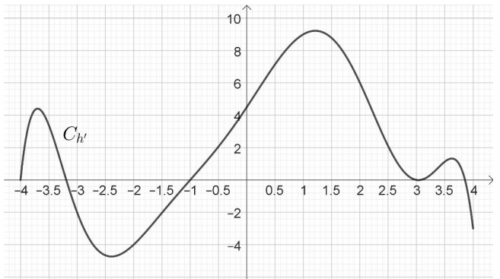
2. Soit une fonction définie et dérivable sur l’intervalle [−4; 4].
La représentation graphique $C_{h'}$ de sa fonction dérivée est donnée ci-dessous.

Affirmation 2 : La fonction est convexe sur [−1; 3].

3. Le code d’un immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis de
deux lettres distinctes parmi A, B et C (exemple : 1232BA).

Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0.

4. On considère la fonction définie sur $]0;+\infty[$ par .

Affirmation 4 : La fonction est une solution sur $]0;+\infty[$ de l’équation différentielle

Exercice 4 : (5 points)
Dans un repère orthonormé $(O,\vec{i},\vec{j},\vec{k})$ de l’espace, on considère le plan d’équation :

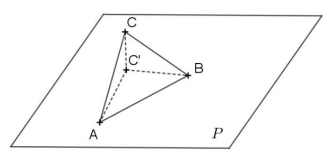
On considère les trois points A, B et C de coordonnées :
A(1 ; 0 ; 1) , B(2 ; − 1 ; 1) et C( − 4 ; − 6 ; 5) .
Le but de cet exercice est d’étudier le rapport des aires entre un triangle et son projeté
orthogonal dans un plan.

Partie A
1. Pour chacun des points A, B et C, vérifier s’il appartient au plan .
2. Montrer que le point $C'(0\,;\,-\,2\,;\,-\,1)$ est le projeté orthogonal du point C sur le plan .
3. Déterminer une représentation paramétrique de la droite (AB).
4. On admet l’existence d’un unique point H vérifiant les deux conditions :

$\{\begin{matrix}\,H\,\in\,(AB)\,\\\,(AB)\,\,et\,\,(HC)\,\,sont\,\,orthogonales.\,\end{matrix}.$

Déterminer les coordonnées du point H.

Partie B
On admet que les coordonnées du vecteur $\vec{HC}$ sont :

$\vec{HC}\begin{pmatrix}\,-\frac{11}{2}\\\\\,-\frac{11}{2}\\\,\\\,4\,\end{pmatrix}$

1. Calculer la valeur exacte de $\,\|\vec{\,HC}\,\,\|$ .
2. Soit l’aire du triangle ABC. Déterminer la valeur exacte de .

Partie C
On admet que $HC'=\sqrt{\frac{17}{2}}$ .

1. Soit $\alpha\,=\widehat{CHC'}$ .

Déterminer la valeur de $cos(\alpha\,)$ .
2.
a. Montrer que les droites et sont perpendiculaires.
b. Calculer l’aire du triangle , on donnera la valeur exacte.

c. Donner une relation entre , et $cos(\alpha\,)$ .

Consulter le corrigé

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «asie Pacifique bac de maths 2024 : sujet n° 2 corrigé» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.