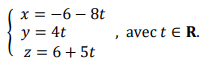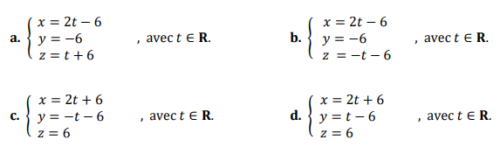Bac de maths 2024 blanc n°3 : sujet et corrigé du bac en PDF.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
SESSION 2024
MATHÉMATIQUES

Durée de l’épreuve : 4 heures

L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire « type collège » est autorisé.
Dès que ce sujet vous est remis, assurez-vous qu’il est complet.
Sauf mention contraire, toute réponse devra être justifiée.
Le candidat est invité à faire figurer sur la copie toute trace de recherche, même
incomplète ou non fructueuse, qu’il aura développée.
La qualité de la rédaction, la clarté et la précision des raisonnements seront prises
en compte dans l’appréciation de la copie. Les traces de recherche, même
incomplètes ou infructueuses, seront valorisées.

Exercice 1 (4 points)
Une concession automobile vend des véhicules à moteur électrique et des véhicules à
moteur thermique.
Certains clients, avant de se rendre sur le site de la concession, ont consulté la plateforme numérique de la concession. On a ainsi observé que :
● 20 % des clients sont intéressés par les véhicules à moteur électrique et 80 %
préfèrent s’orienter vers l’achat d’un véhicule à moteur thermique ;
● lorsqu’un client souhaite acheter un véhicule à moteur électrique, la probabilité
pour que le client ait consulté la plate-forme numérique est de 0,5 ;
● lorsqu’un client souhaite acheter un véhicule à moteur thermique, la probabilité
pour que le client ait consulté la plate-forme numérique est de 0,375.
On considère les événements suivants :
● C : « un client a consulté la plate-forme numérique » ;
● E : « un client souhaite acquérir un véhicule à moteur électrique » ;
● T : « un client souhaite acquérir un véhicule à moteur thermique ».
Les clients font des choix indépendants les uns des autres.
1.
a. Calculer la probabilité qu’un client choisi au hasard souhaite acquérir un
véhicule à moteur électrique et ait consulté la plate-forme numérique.
On pourra utiliser un arbre pondéré.
b. Démontrer que (C) = 0,4.
c. On suppose qu’un client a consulté la plate-forme numérique.
Calculer la probabilité que le client souhaite acheter un véhicule à moteur
électrique.
2. La concession accueille quotidiennement 17 clients en moyenne.
On note X la variable aléatoire donnant le nombre de clients souhaitant acquérir
un véhicule à moteur électrique.
a. Préciser la nature et les paramètres de la loi de probabilité suivie par X.
b. Calculer la probabilité qu’au moins trois des clients souhaitent acheter un
véhicule à moteur électrique lors d’une journée.

Donner le résultat arrondi à 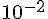$10^{-2}$ près.

Exercice 2 (6 points)
Les parties A et B peuvent être traitées indépendamment.

Partie A
On considère la fonction définie sur $\mathbb{R}$ par
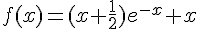$f(x)=(x+\frac{1}{2})e^{-x}+x$ .
1. Déterminer les limites de en 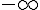$-\infty$ et en $+\infty$ .
2. On admet que est deux fois dérivable sur $\mathbb{R}$ .
a. Démontrer que, pour tout ∈ $\mathbb{R}$ ,
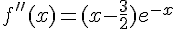$f''(x)=(x-\frac{3}{2})e^{-x}$ .
b. En déduire les variations et le minimum de la fonction ′ sur $\mathbb{R}$ .
c. Justifier que pour tout ∈ $\mathbb{R}$ , ′() > 0.
d. En déduire que l’équation () = 0 admet une unique solution sur $\mathbb{R}$ .
e. Donner une valeur arrondie à 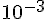$10^{-3}$ de cette solution.

Partie B
On considère une fonction , définie et dérivable sur $\mathbb{R}$ , ayant une expression de
la forme 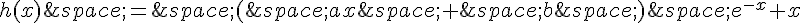$h(x)\,=\,(\,ax\,+\,b\,)\,e^{-x}+x$ , où et sont deux réels.
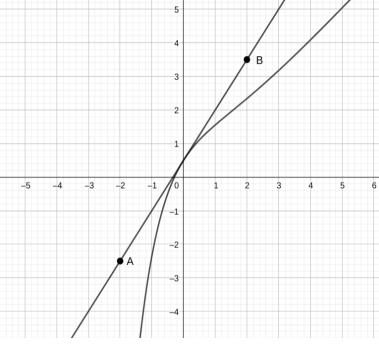
Dans un repère orthonormé ci-après figurent :
● la courbe représentative de la fonction ℎ ;
● les points A et B de coordonnées respectives (-2 ; -2,5) et (2 ; 3,5)

1. Conjecturer, avec la précision permise par le graphique, les abscisses des
éventuels points d’inflexion de la courbe représentative de la fonction ℎ.
2. Sachant que la fonction h admet sur $\mathbb{R}$ une dérivée seconde d’expression
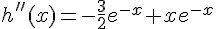$h''(x)=-\frac{3}{2}e^{-x}+xe^{-x}$ , valider ou non la conjecture précédente.
3. Déterminer une équation de la droite (AB).
4. Sachant que la droite (AB) est tangente à la courbe représentative de la fonction
ℎ au point d’abscisse 0, en déduire les valeurs de et .

Exercice 3 (5 points)
On considère la fonction définie sur $\mathbb{R}$ par
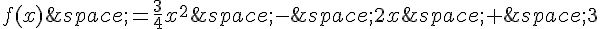$f(x)\,=\frac{3}{4}x^2\,-\,2x\,+\,3$ .
1. Dresser le tableau de variations de sur $\mathbb{R}$ .
2. En déduire, que pour tout appartenant à l’intervalle $[\frac{4}{3};\,2]$ , () appartient à
l’intervalle $[\frac{4}{3};\,2]$ .
3. Démontrer que pour tout réel, 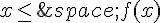$x\leq\,\,f(x)$ .
Pour cela, on pourra démontrer que pour tout réel :
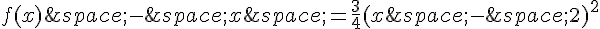$f(x)\,-\,x\,=\frac{3}{4}(x\,-\,2)^2$ .
On considère la suite (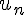) définie par un réel 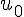et pour tout entier naturel :

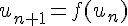
$u_{n+1}=f(u_n)$

On a donc, pour tout entier naturel ,

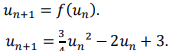
4. Etude du cas : 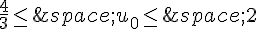$\frac{4}{3}\leq\,\,u_0\leq\,\,2$ .
a. Démontrer par récurrence que, pour tout entier naturel ,
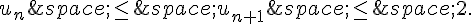
$u_n\,\leq\,\,u_{n+1}\,\leq\,\,2.$
b. En déduire que la suite (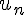) est convergente.
c. Prouver que la limite de la suite est égale à 2.

5. Etude du cas particulier : 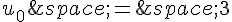$u_0\,=\,3$ .
On admet que dans ce cas la suite (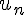) tend vers $+\infty$ .
Recopier et compléter la fonction « seuil » suivante écrite en Python, afin qu’elle
renvoie la plus petite valeur de telle que 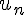soit supérieur ou égal à 100.

6. Etude du cas : 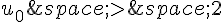$u_0\,>\,2$ .
À l’aide d’un raisonnement par l’absurde, montrer que (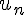) n’est pas convergente.

Exercice 4 (5 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes,
une seule des quatre réponses proposées est exacte. Une réponse fausse, une réponse
multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point. Pour
répondre, indiquer sur la copie le numéro de la question traitée et la lettre de la réponse
choisie. Aucune justification n’est demandée.

L’espace est muni d’un repère orthonormé 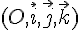$(O,\vec{i},\vec{j},\vec{k})$ dans lequel on considère :
• les points (6 ; −6 ; 6), (−6 ; 0 ; 6) et (−2 ; −2 ; 11) ;
• la droite () orthogonale aux deux droites sécantes () et () et passant par
le point ;
• la droite (′) de représentation paramétrique :

Question 1
Parmi les vecteurs suivants, lequel est un vecteur directeur de la droite () ?

Question 2
Parmi les équations suivantes, laquelle est une représentation paramétrique de la droite
(AB) ?

Question 3
Un vecteur directeur de la droite 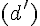est :

Question 4
Lequel des quatre points suivants appartient à la droite ?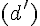

a. 1 (50; −28; −29) b. 2 (−14; −4; 1) c. 3 (2; −4; −1) d. 4 (−3; 0; 3)

Question 5
Le plan d’équation = 1 a pour vecteur normal :

Consulter le corrigé

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac de maths 2024 blanc n°3 : sujet et corrigé du baccalauréat en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.