Fonction continue : cours de maths en terminale en PDF.

Sommaire

La continuité d’une fonction numérique dans un cours de maths en terminale faisant intervenir le théorème des valeurs intermédiaires. Nous terminerons cette leçon par l’interprétation graphique et les propriétés de la continuité.

Remarque :

Les programmes limitent la continuité à une approche intuitive qui est de considérer qu’une fonction est continue sur un intervalle I si sa courbe représentative sur I peut être tracée entièrement sans lever le crayon.

I. Notion de continuité d’une fonction.

Propriétés : (admise)

Les fonctions usuelles (affines, carré, inverse, racine carrée, valeur absolue) sont continues
sur tout intervalle inclus dans leur ensemble de définition.
Toute fonction construite algébriquement (par somme, produit, inverse ou composée) à
partir de fonctions usuelles est continue sur tout intervalle de son ensemble de définition.
On convient qu’une flèche oblique dans un tableau de variation traduit la continuité et la
stricte monotonie de la fonction sur l’intervalle considéré.
Une fonction dérivable sur un intervalle est continue sur cet intervalle.

Remarque :

Attention, la réciproque de cette dernière propriété est fausse.
Par exemple, la fonction valeur absolue $x\,\mapsto \,\,|x\,\,|$ est continue en 0 mais non dérivable en 0.

Méthode : interpréter graphiquement la continuité d’une fonction.
Par convention, une fonction est continue là où elle est tracée. S’il n’y a pas continuité en :

le symbole bille rouge indique le point de la courbe de coordonnées ( ; f ()) ;
le symbole bille rose vide indique un point qui n’appartient pas à la courbe mais dont l’ordonnée est égale à la limite à gauche ou à droite en .

Exercice d’application :

Déterminer graphiquement les intervalles sur lesquels f est continue.
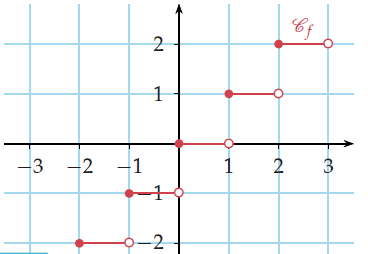
1) Soit la fonction partie entière f : $x\,\mapsto \,\,|x\,\,|$ .

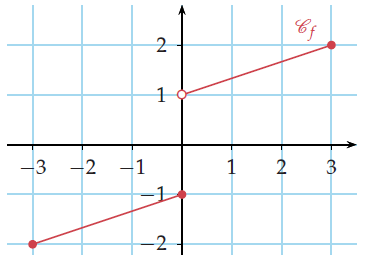
2) Soit la fonction f représentée ci-dessous.

II. Théorème des valeurs intermédiaires.

Théorème : cas général.

Soit f une fonction définie sur un intervalle I contenant deux réels a et b tels que a < b.
Si f est continue sur [a ; b], alors pour tout réel k compris entre f (a) et f (b), il existe au moins
un réel c appartenant à [a ; b] tel que f (c) = k.

Remarque :
f prend au moins une fois toute valeur intermédiaire entre f (a) et f (b).
Autrement dit, l’équation f (x) = k a au moins une solution dans [a ; b] et, sur [a ; b], la
courbe représentative de f coupe la droite d’équation y = k en un point au moins.

Exemple :

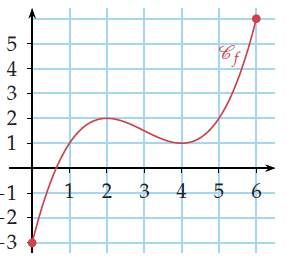
Soit f la fonction définie sur [0 ; 6] par $f\,(x)\,=\frac{x^3}{4}-\frac{9}{4}x^2\,+\,6x\,-\,3$ .

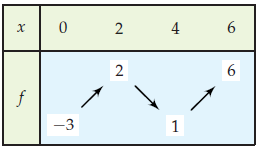
On dresse le tableau de variation de f . f admet pour minimum −3 et pour maximum 6.
f est continue sur [0 ; 6].

Donc, d’après le théorème des valeurs intermédiaires, f prend toutes les valeurs de [−3 ; 6]. En particulier, l’équation f (x) = 0 a au moins une solution dans [0 ; 6].

Théorème : cas d’une fonction strictement monotone.

Soit f une fonction définie sur un intervalle I contenant deux réels a et b tels que a < b.
Si f est continue et strictement monotone sur [a ; b], alors pour tout réel k compris entre f (a)
et f (b), il existe un unique réel c appartenant à [a ; b] tel que f (c) = k.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonction continue : cours de maths en terminale en PDF.» au format PDF.

D'autres cours et exercices à consulter

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.