Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.

Mis à jour le 2 avril 2025

✏️Exercices

Terminale • Lycée

Les fonctions sinus et cosinus

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les fonctions sinus et cosinus avec des exercices de maths en terminale corrigés en PDF. Utilisation des propriétés et de la périodicité de ces fonctions.

Exercice 1 :

Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur $\mathbb{R}$ par :
a) $f(x)\,=\,x\,+\,cos\,(x)$
b) $g(x)=\,x\,cos\,(x)$

Exercice 2 :
Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur $\mathbb{R}$ par :
$a)\,f(x)=\,sin(x)\,+\,cos(x)$

$b)\,g(x)=\,sin\,(x)\,-cos(x)$

Exercice 3 :

Résoudre dans l’intervalle $[-\pi\,;\,\pi]$ :
a. $cos(x)=\frac{\sqrt{2}}{2}$

b. $cos(x)\,\leq\,\,\frac{\sqrt{2}}{2}$

Exercice 4 :
Résoudre dans l’intervalle $[-\pi\,;\,\pi]$ :
a. $cos(x)=-\frac{1}{2}$

b. $cos(x)\,\geq\,\,-\frac{1}{2}$

Exercice 5 :

1. Démontrer que l’équation $cos(x)\,=\,x$ admet une unique solution dans $[0;\frac{\pi}{2}]$ .
2. On étudie la fonction Balayage ci-dessous, écrite en langage Python.

a) Exécuter pas à pas ce programme et compléter un tableau de suivi de la
de variable a pour p = 0,1.

Faire apparaitre également dans ce tableau.
Arrondir au centième.
Quelles sont les valeurs obtenues ?
b) Expliquer le rôle de ce programme.
c) Saisir ce programme et l’exécuter avec $p\,=\,0,000\,1$ .

Interpréter le résultat obtenu.

Exercice 6 :

f est la fonction définie sur $\mathbb{R}$ par :

Laquelle de ces affirmations est exacte ?
(1) La fonction f est paire.
(2) La fonction f est impaire.
(3) La fonction f n’est ni paire ni impaire.

Exercice 7 :

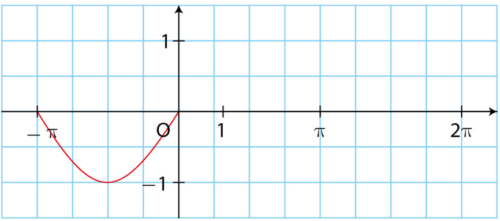
Voici la courbe représentative de la fonction sinus sur $[-\pi\,;\,0]$ dans un repère.
Expliquer oralement comment compléter cette courbe pour l’obtenir sur $[-\pi\,;\,2\pi]$ .

Exercice 8 :

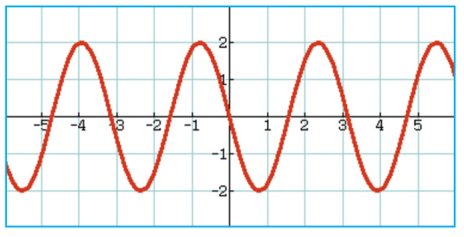
Voici la courbe représentative de la fonction g définie sur $\mathbb{R}$ par .

1. a) Conjecturer graphiquement la parité de g.
b) Exprimer en fonction de et démontrer cette conjecture.
2.Exprimer $g(x\,+\,\pi)$ en fonction de et démontrer que la fonction g est périodique de période $\pi$ .

Exercice 9 :

h est la fonction définie sur $\mathbb{R}$ par :
$h(x)=\,sin(x)\,+\,sin(2x).$
a) Démontrer que la fonction h est impaire.
b) Qu’en déduit-on pour sa courbe représentative $(\varphi\,)$ dans un repère ?
c) Afficher la courbe $(\varphi\,)$ à l’écran de la calculatrice et vérifier cette conjecture.

Exercice 10 :

Dans chaque cas, déterminer la fonction dérivée de la fonction définie sur I.

$a)g(x)=\frac{sin(x)}{x}\,\,,\,\,I=]0;+\infty[$

$b)\,h(x)=\frac{1}{sin(x)}\,,\,\,I=]0;+\pi[$

Exercice 11 :

f est la fonction définie sur $\mathbb{R}$ par :
$f(x)=\,sin^2(x)\,+\,2sin(x).$

1.Montrer que pour tout x, $f'(x)=\,2(sin(x)\,+\,1)cos(x)$ .

2.a) Expliquer pourquoi est du signe de sur $[0\,;\pi].$

En déduire le signe de sur $[0\,;\pi].$

b) Dresser le tableau de variations de f sur $[0\,;\pi].$

Exercice 12 :

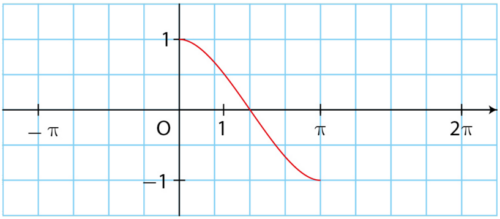
On a tracé ci-dessous la courbe représentative de la fonction cosinus sur l’intervalle $[0\,;\pi].$
Expliquer oralement comment compléter cette courbe pour l’obtenir sur $[-\pi\,;2\pi].$

Exercice 13 :

f est la fonction définie sur $\mathbb{R}$ par :
$f\,(x)\,=cos(2x)\,+\,cos(3x).$
Voici ci-dessous un écran de calcul formel.

a) Vérifier les résultats.
b) Quelles propriétés de la fonction f observe-t-on ainsi ?
c) Qu’en déduit-on pour la courbe représentative de f ?

Exercice 14 :

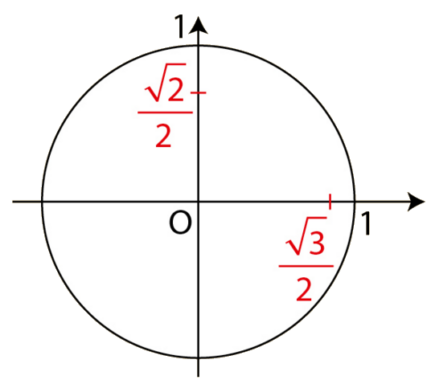
S’aider de ce cercle trigonométrique pour indiquer mentalement
les solutions dans $[-\frac{\pi}{2};\frac{\pi}{2}]$ de l’équation :
$a)\,cos(x)=\frac{\sqrt{3}}{2}$

$b)\,sin(x)=\frac{\sqrt{2}}{2}$

Exercice 15 :

L’Université de Manchester a mis au point une plate-forme équipée de flotteurs pour capturer l’énergie des vagues.
L’oscillation de la houle à la surface de l’eau induit l’oscillation verticale des flotteurs.

La distance d du fond marin au centre de flottaison d’un flotteur est donnée en fonction du temps t sur par :
$d(t)\,=\,1,5cos\,(\,\frac{\pi}{2}t)\,+\,50$
où d(t) est exprimé en mètre et t en seconde.
1. Déterminer l’amplitude du mouvement du flotteur.

2. a) Déterminer sur .
b) Expliquer pourquoi est négatif sur $[0\,;\,2]$ et positif sur [2 ; 4].
c) Dresser le tableau de variations de d sur .
d) Sur quel intervalle de temps le flotteur monte-t-il ?
3. On se propose de déterminer à quel(s) instant(s) de l’intervalle , la vitesse du flotteur est maximum.
On rappelle que la vitesse à l’instant t est $v(t)\,=d'(t)$ .
a) Déterminer la dérivée seconde sur .
b) Donner un encadrement de $\frac{\pi}{2}t$ pour $t\,\in\,[0\,;\,4]$ , puis résoudre l’équation $cos\,(\,\frac{\pi}{2}t)\,=0$ dans cet intervalle.
c) Dresser le tableau de variations de la vitesse du flotteur sur .

En déduire l’instant t de où la vitesse du flotteur est maximum.

4.2/5 - (20342 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les fonctions sinus et cosinus : exercices de maths en terminale en PDF.» au format PDF.

Ressources de terminale

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Les fonctions sinus et cosinus : exercices de maths en terminale en PDF.

Ressources de terminale

Cours de terminale

Exercices de terminale

Baccalauréat

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques