Calculs d'intégrales : cours de maths en terminale à télécharger.

Les calculs d’intégrales à travers un cours de maths en terminale. Nous considèrerons une fonction positive et continue et la dérivabilité d’une fonction définie par une intégrale puis la primitive d’une fonction continue.Une synthèse des primitives des fonctions usuelles et la linéarité de l’intégrale ainsi que la relation de Chasles et l’aire entre deux courbes.
Connaissances nécessaires à ce chapitre

Calculer l’aire des polygones usuels;
Effectuer des conversions d’unités d’aire;
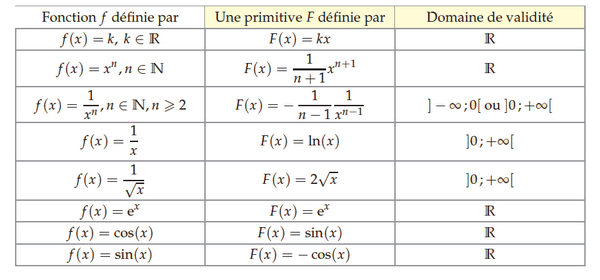
Dériver les fonctions usuelles;
Représenter et décrire un domaine du plan.

Définition

Soit (O; $\vec{i}$ , $\vec{j}$ ) un repère orthogonal du plan.
On note I et J les points tels que $\vec{OI}=\vec{i}$ et $\vec{OJ}=\vec{j}$ .
L’unité d’aire, que l’on note u.a., est l’aire du rectangle dont O, I et J forment trois sommets.

I. Intégrale d’une fonction continue et positive.

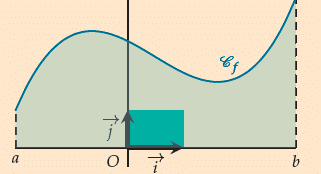
Définition : notion d’intégrale.

Soit f une fonction continue et positive sur un intervalle [a ; b] de courbe représentative

dans un repère orthogonal (O; $\vec{i}$ , $\vec{j}$ ).
L’intégrale de a à b de f est l’aire, exprimée en unités d’aire, du domaine situé entre la courbe

, l’axe des abscisses et les droites d’équation x = a et x = b.
Cette aire se note $\int_{a}^{b}f(x)dx$ et on prononce « intégrale (ou somme) de a à b de f (x) dx ».

Remarques :

a et b s’appellent respectivement « borne inférieure » et « borne supérieure » de l’intégrale.
La valeur de l’intégrale ne dépend que de a, b et f ; la variable x n’intervenant pas dans le
résultat, on dit qu’elle est muette et l’on peut donc noter indifféremment :
$\int_{a}^{b}f(x)dx=\int_{a}^{b}f(t)dt=\int_{a}^{b}f(u)du=...$
Pour toute fonction f continue et positive en un réel a, $\int_{a}^{a}f(x)dx=0$ puisqu’il s’agit de
l’aire d’un segment de hauteur f (a).
Le symbole $\int$ est dû à Leibniz, (1646-1716). Il ressemble à un « s » allongé, rappelant
que l’aire peut être calculée comme la somme de petites aires élémentaires.

Théorème : dérivabilité d’une fonction définie par une intégrale.

Soit f une fonction continue et positive sur un intervalle [a ; b].
La fonction $F\,:\,x\,\mapsto \,\int_{a}^{x}f\,(t)\,dt$ est définie et dérivable sur [a ; b] et on a F′ = f .

II. Primitives d’une fonction continue.

Définition

Soit f une fonction définie et continue sur un intervalle I.
Une primitive de f sur I est une fonction F définie et dérivable sur I telle que F′ = f .

Remarques :

On dit que F est une primitive de f et non pas la primitive de f car une fonction
admettant une primitive n’en admet pas une seule, comme le montre l’exemple ci-dessous.

Exemple :

Soit $f\,:x\,\mapsto \,2x$ définie sur $\mathbb{R}$ . Alors $F_1:x\,\mapsto \,x^2$ est une primitive de f sur $\mathbb{R}$ .
De même, $F_2:x\,\mapsto \,x^2+1$ est aussi une primitive de f sur $\mathbb{R}$ . On a $F'_1\,=\,F'_2\,=\,f$ .

Théorème : existence de primitives.

Toute fonction continue sur un intervalle I admet des primitives sur I.

Théorème : Lien entre les primitives.

Soit f une fonction définie et continue sur un intervalle I et F une primitive de f sur I.
Alors f admet une infinité de primitives sur I qui sont toutes de la forme
$x\,\mapsto \,F(x)\,+\,k,\,k\,\in\,\mathbb{R}$ .

Propriété : condition d’unicité de la primitive.

Soient $x_0\,\in\,I$ et

deux réels donnés. Parmi toutes les primitives d’une fonction f définie et
continue sur I, il en existe une seule qui vérifie la condition $F(x_0)\,=\,y_0$ .

Remarque :
Pour tout $x_0\,\in\,I$ et $F\,:\,x\,\mapsto \,\int_{x_0}^{x}f\,(t)\,dt$ est donc la primitive de f sur I s’annulant
en .

En effet, F est bien une primitive de f sur I et c’est la seule vérifiant la condition $F(x_0)\,=\,0$ .

Propriété : calcul pratique d’une intégrale.

Soit f une fonction continue et positive sur [a ; b] et F une primitive de f sur [a ; b]. Alors :
$\int_{a}^{b}f(x)dx=F(b)-F(a)$ .

Exemple :

On souhaite calculer $\int_{0}^{1}x^2dx$ . Pour cela, posons $f\,:x\,\mapsto \,x^2$ , définie sur [0 ; 1].
En remarquant que $F\,:\,x\,\mapsto \,\frac{x^3}{3}$ est une primitive de f sur [0 ; 1], on obtient :
$\int_{0}^{1}x^2dx=\frac{1^3}{3}-\frac{0^3}{3}=\frac{1}{3}$

Propriété : primitives des fonctions usuelles.

Propriété : primitives et opérations sur les fonctions.

Soient u et v deux fonctions dérivables sur un intervalle I.

III. Intégrale d’une fonction continue de signe quelconque.

On a vu au paragraphe précédent que, pour une fonction continue et positive sur [a ; b] :
$\int_{a}^{b}f(x)dx=F(b)-F(a)$ où F est une primitive de f sur [a ; b].

On étend cette propriété aux fonctions de signe quelconque, continues sur un intervalle [a ; b] avec la définition ci-dessous.

Définition :

Soit f une fonction continue sur un intervalle [a ; b] et de signe quelconque et F une primitive
de f sur [a ; b]. On pose : $\int_{a}^{b}f(x)dx=F(b)-F(a)$ .

Exemple :

On souhaite calculer $\int_{-1}^{2}(x^2\,-\,2)\,dx$ . Pour cela, on pose $f\,:\,x\,\mapsto \,x^2\,-\,2$ définie sur
I = [−1 ; 2].

Une primitive de f sur I est $F:x\,\mapsto \,\frac{x^3}{3}-2x$ et on obtient alors :

$\int_{-1}^{2}(x^2\,-\,2)\,dx=(\,\frac{2^3}{3}-2\times \,2\,)-(\,\frac{(-1)^3}{3}-2\times \,(-1))=-3$ .

Propriété : linéarité de l’intégrale.

Soient f et g deux fonctions continues sur un intervalle [a ; b] et l un réel.Alors :

$\int_{a}^{b}(f+g)(t)dt=\,\int_{a}^{b}f(t)dt+\,\int_{a}^{b}g(t)dt$ .

$\int_{a}^{b}(\alpha\,f)(t)dt=\alpha\int_{a}^{b}\,f(t)dt$

Propriété : fonction négative et aire.

Soit f une fonction continue et négative sur un intervalle [a ; b]. Alors, l’aire du domaine situé
entre

et l’axe des abscisses, sur l’intervalle [a ; b] est $-\int_{a}^{b}f(x)dx$ .

Preuve :

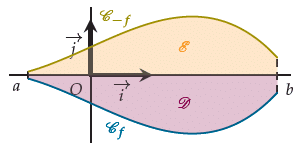
On note D le domaine situé entre Cf et l’axe des abscisses, sur [a ; b].
Par symétrie par rapport à l’axe des abscisses, l’aire de D est égale à l’aire du domaine E , compris entre la courbe de −f et l’axe des abscisses, sur l’intervalle [a; b].

Ainsi :

$A_D=A_E=\int_{a}^{b}(-f)(x)dx=-\int_{a}^{b}f(x)dx$ .

Propriété : relation de Chasles

Soient f une fonction continue sur un intervalle I et a, b, c, trois réels appartenant à I. Alors :
$\int_{a}^{c}f(x)dx=\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx$

Preuve :

f étant une fonction continue sur I, elle admet une primitive sur cet intervalle.
Notons F une primitive de f sur I.

Pour démontrer l’égalité annoncée, calculons séparément chaque membre de l’égalité :
$\int_{a}^{c}f(x)dx=F(c)-F(a)$ par définition.
$\int_{a}^{b}f(x)dx+\int_{b}^{c}f(x)dx=\,F(b)\,-\,F(a)\,+\,F(c)\,-\,F(b)\,=\,F(c)\,-\,F(a)$ toujours par définition
puis en réduisant l’expression obtenue.

L’égalité annoncée est donc vraie.

Propriété

Soient f et g deux fonctions continues sur un intervalle [a ; b] telles que f > g. Alors, l’aire
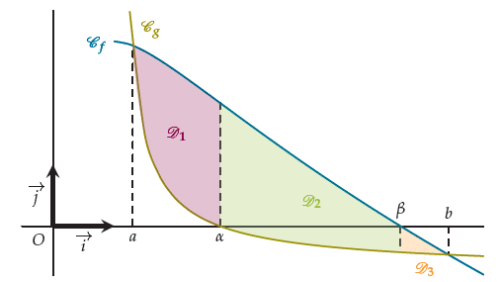
du domaine compris entre les courbes Cf et Cg sur [a ; b] est donnée par $\int_{a}^{b}(\,f\,-\,g)(x)\,dx$ .

Propriété : intégrales et inégalités.

Soient f et g deux fonctions continues sur un intervalle [a ; b]. Alors :

Si f est positive sur [a ; b], alors $\int_{a}^{b}f(x)dx\geq\,\,0$ .
Si pour tout $x\in[a;b]$ , $f(x)\leq\,\,g(x)$ , alors $\int_{a}^{b}f(x)dx\leq\,\,\int_{a}^{b}g(x)dx$ .

Définition : valeur moyenne.

Soit f une fonction continue sur un intervalle [a ; b].La valeur moyenne de f sur [a ; b] est le nombre $\mu$ défini par :

$\mu\,=\frac{1}{b-a}\int_{a}^{b}f(t)dt$

Remarque :
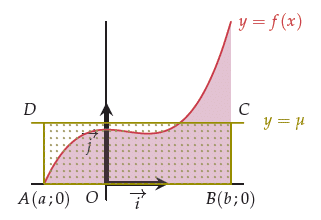
Dans le cas où f est positive et continue sur [a ; b], la valeur moyenne de f entre a et b représente la hauteur du rectangle construit sur l’intervalle [a ; b].
L’aire du rectangle ABCD est égale, en u.a., à l’aire du domaine coloré car d’après la définition :

$(b-a)\mu\,=\int_{a}^{b}f(t)dt$

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calculs d'intégrales : cours de maths en terminale en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.