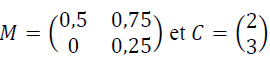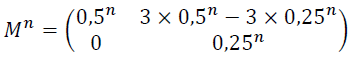Bac S Liban 2019 : sujet et corrigé à télécharger en PDF

MATHÉMATIQUES
Série S
Enseignement de spécialité – Coefficient 9
Durée de l’épreuve : 4 heures

Exercice n°1 (5 points)
Commun à tous les candidats
Le plan est muni d’un repère orthogonal (O, I, J).
1. On considère la fonction définie sur l’intervalle ]0 ;1] par .
a. Déterminer une expression de la fonction dérivée de et vérifier que pour tout ∈ ]0 ;1], ′()=(ln+1)(ln−1).
b. Étudier les variations de la fonction f et dresser son tableau de variations sur l’intervalle ]0 ;1] (on admettra que la limite de la fonction f en 0 est nulle).
On note Γ la courbe représentative de la fonction g définie sur l’intervalle ]0 ;1] par ()=ln. Soit un réel de l’intervalle ]0 ;1].

On note M le point de la courbe Γ d’abscisse et la tangente à la courbe Γ au point M. Cette droite coupe l’axe des abscisses au point N, et l’axe des ordonnées au point P .
On s’intéresse à l’aire du triangle ONP quand le réel a varie dans l’intervalle ]0 ;1].

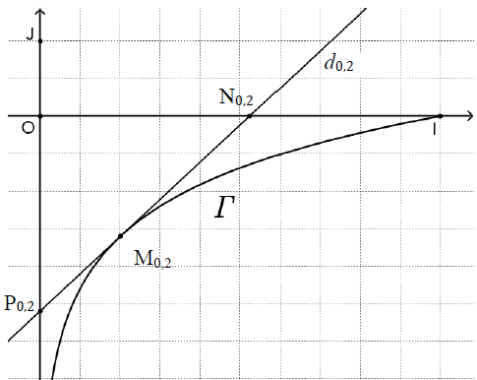
2. Dans cette question, on étudie le cas particulier où =0,2 et on donne la figure ci-dessous.

a. Déterminer graphiquement une estimation de l’aire du triangle ON0,2P0,2 en unités d’aire.
b. Déterminer une équation de la tangente 0,2 .
c. Calculer la valeur exacte de l’aire du triangle ON0,2P0,2 .
Dans ce qui suit, on admet que, pour tout réel de l’intervalle ]0 ;1], l’aire du triangle ONP en unités d’aire est donnée par $A(a)=\frac{1}{2}a,(1,-lna)^2$ .
3. À l’aide des questions précédentes, déterminer pour quelle valeur de l’aire () est maximale. Déterminer cette aire maximale.

Exercice n°2 (4 points)
Commun à tous les candidats
Le plan complexe est muni d’un repère orthonormé direct $(O,\vec{u},\vec{v})$ d’unité 2 cm. On appelle la fonction qui, à tout point M, distinct du point O et d’affixe un nombre complexe , associe le point M′ d’affixe ′ tel que $z'=\frac{-1}{z}$ .
1.On considère les points A et B d’affixes respectives et $z_B=\frac{1}{2}e^{i\frac{\pi}{3}}$ .

a.Déterminer la forme algébrique de l’affixe du point A′ image du point A par la fonction .
b.Déterminer la forme exponentielle de l’affixe du point B′ image du point B par la fonction .
c.Sur la copie, placer les points A,B,A′ et B′ dans le repère orthonormé direct $(O,\vec{u},\vec{v})$ .

Pour les points B et B′, on laissera les traits de construction apparents.
2.Soit un réel strictement positif et un réel. On considère le complexe défini par $z=re^{i\theta,}$ .
a.Montrer que $z'=\frac{1}{r}e^{i(\pi-,\theta,)}$ .
b.Est-il vrai que si un point M, distinct de O, appartient au disque de centre O et de rayon 1 sans appartenir au cercle de centre O et de rayon 1, alors son image M′ par la fonction est à l’extérieur de ce disque ? Justifier.

3.Soit le cercle $\sigma$ de centre K d’affixe $z_K=-\frac{1}{2}$ et de rayon $\frac{1}{2}$ .
a.Montrer qu’une équation cartésienne du cercle $\sigma$ est .
b.Soit =+i avec et non tous les deux nuls. Déterminer la forme algébrique de ′ en fonction de x et y.
c.Soit M un point, distinct de O, du cercle $\sigma$ .

Montrer que l’image M′ du point par la fonction appartient à la droite d’équation =1.

Exercice n°3 (6 points)
Commun à tous les candidats
Les parties A et B peuvent être traitées de façon indépendante.
Partie A
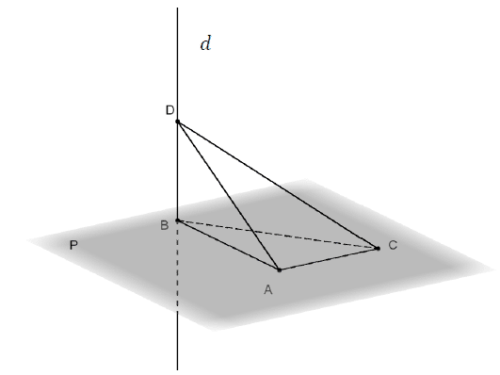
Dans un plan , on considère un triangle ABC rectangle en A.
Soit la droite orthogonale au plan et passant par le point B. On considère un point D de cette droite distinct du point B.

1. Montrer que la droite (AC) est orthogonale au plan (BAD).
On appelle bicoin un tétraèdre dont les quatre faces sont des triangles rectangles.
2. Montrer que le tétraèdre ABCD est un bicoin.
3. a. Justifier que l’arête [CD] est la plus longue arête du bicoin ABCD.
b. On note I le milieu de l’arête [CD]. Montrer que le point I est équidistant des 4 sommets du bicoin ABCD.

Partie B
Dans un repère orthonormé de l’espace, on considère le point A (3 ;1 ;−5)et la droite de représentation paramétrique $\{,x=2t+1\begin{matrix},,y=-2t+9,,\\,,z=t-3,,\end{matrix}.$ où $t\in,\mathbb{R}$ .
1. Déterminer une équation cartésienne du plan orthogonal à la droite et passant par le point A.
2. Montrer que le point d’intersection du plan et de la droite est le point B(5 ;5 ;−1).
3. Justifier que le point C (7 ;3 ;−9) appartient au plan puis montrer que le triangle ABC est un triangle rectangle isocèle en A.
4. Soit t un réel différent de 2 et M le point de paramètre appartenant à la droite .
a. Justifier que le triangle ABM est rectangle.
b. Montrer que le triangle ABM est isocèle en B si et seulement si le réel vérifie l’équation .
c. En déduire les coordonnées des points M1 et M2 de la droite tels que les triangles rectangles ABM1 et ABM2 soient isocèles en B.

Partie C
On donne le point D(9 ; 1 ; 1) qui est un des deux points solutions de la question 4.c. de la partie B.
Les quatre sommets du tétraèdre ABCD sont situés sur une sphère. En utilisant les résultats des questions des parties A et B précédentes, déterminer les coordonnées du centre de cette sphère et calculer son rayon.

Exercice n°4 (5 points)
Candidats ayant suivi l’enseignement de spécialité
Dans un jardin public, un artiste doit installer une oeuvre aquatique commandée par la mairie. Cette oeuvre sera constituée de deux bassins A et B ainsi que d’une réserve filtrante R. Au départ, les deux bassins contiennent chacun 100 litres d’eau. Un système de canalisations devra alors permettre de réaliser, toutes les heures et dans cet ordre, les transferts d’eau suivants :
– dans un premier temps, la moitié du bassin A se vide dans la réserve R ;
– ensuite, les trois quarts du bassin B se vident dans le bassin A ;
– enfin, on rajoute 200 litres d’eau dans le bassin A et 300 litres d’eau dans le bassin B.

Une étude de faisabilité du projet amène à étudier la contenance des deux bassins A et B qui est à prévoir pour éviter tout débordement.
On modélise les quantités d’eau des deux bassins A et B à l’aide de deux suites et : plus précisément pour tout entier naturel , on note et les quantités d’eau en centaines de litres qui seront respectivement contenues dans les bassins A et B au bout de heures. On suppose pour cette étude mathématique que les bassins sont a priori suffisamment grands pour qu’il n’y ait pas de débordement.
Pour tout entier naturel , on note la matrice colonne .

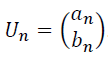
Ainsi .
1. Justifier que, pour tout entier naturel n, $U_{n+1}=MU_n+C$

où

.
2. On considère la matrice

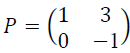
a. Calculer . En déduire que la matrice est inversible et préciser sa matrice inverse.
b. Montrer que est une matrice diagonale que l’on précisera.
c. Calculer .
d. Démontrer par récurrence que, pour tout entier naturel , .
On admet par la suite que pour tout entier naturel n,

3. Montrer que la matrice

vérifie .
4. Pour tout entier naturel , on définit la matrice par .
a. Montrer que tout entier naturel , $V_{n+1}=MV_n$ .
b. On admet que, pour tout entier naturel non nul , .
b. Montrer que pour tout entier naturel non nul ,

.
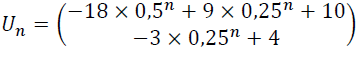
5. a. Montrer que la suite est croissante et majorée. Déterminer sa limite.
b. Déterminer la limite de la suite .
c. On admet que la suite est croissante.

En déduire la contenance des deux bassins A et B qui est à prévoir pour la faisabilité du projet, c’est-à-dire pour éviter tout débordement.

Consulter le corrigé en ligne

Vous pouvez télécharger le sujet du bac S de maths 2019 en Amérique du nord au format PDF.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac S Liban 2019 : sujet et corrigé à télécharger en PDF» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.