Barycentre : exercices de maths en terminale corrigés en PDF.

exercices de maths en terminale S

Des exercices de maths en terminale sur le barycentre de n points pondérés, ces documents peuvent être téléchargés au format PDF puis vous pourrez les imprimer librement à domicile. Vous pouvez également essayer de résoudre les exercices corrigés en terminale en PDF .

Exercice 1

Soit ABC un triangle, D la barycentre de (A,1)(B,2)(C,3), E le barycentre de (A,2)(B,3)(C,1) et F le barycentre de (A,3)(B,1)(C,2).
Montrer que le centre de gravité du triangle ABC est aussi le centre de gravité du triangle DEF.

Exercice 2

A et B sont deux points distincts.
On considère C le barycentre de (A,2)(B,3) et D le barycentre de (A,3)(B,2).
a) Déterminer la nature de l’ensemble des points M tels que 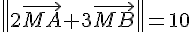$\| 2\vec{MA}+3\vec{MB} \|=10$ .

b) Déterminer la nature de l’ensemble des points M tels que :

$\| 2\vec{MA}+3\vec{MB} \|= \| 3\vec{MA}+2\vec{MB} \|$

Exercice 3

Soit ABC un triangle .
a) Déterminer la nature de l’ensemble des points M tels que 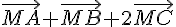$\vec{MA}+\vec{MB}+2\vec{MC}$ soit colinéaire à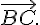 $\vec{BC}.$

b) Déterminer la nature de l’ensemble des points M tels que

$\| \vec{MA}+\vec{MB}+2\vec{MC} \|= \| \vec{MA}+\vec{MB}-2\vec{MC} \|$

Exercice 4

A, B, C et D sont quatre points distincts.
On note K le barycentre de (A,3)(B,1), J le milieu de [DC], G le centre de gravité de BCD et I le milieu de [AG].
Montrer que les points I, J et K sont alignés.

Exercice 5

Soit ABCD un parallélogramme de centre O, G le barycentre de (A,2)(B,1) et H le barycentre de (C,2)(D,1).
a) Montrer que les droites (AC), (BD) et (GH) sont concourantes.
b) Soit E le barycentre de (G,3)(D,1). Montrer que E est le milieu de [AO].

Exercice 6

1. Construire le barycentre des points {(A,1);(B,2)} sachant que AB = 6 cm .
2. Construire le barycentre des points {(A,3);(B,-3)} sachant que AB = 8 cm .

3. Construire le barycentre des points {(A,1);(B,-2)} sachant que AB = 4 cm .

4. Construire le barycentre des points {(M,-3);(N,-2)} sachant que MN = 10 cm .

Exercice 7

1. Décrire l’ensemble des points M du plan tels que 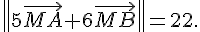$\|5\vec{MA}+6\vec{MB}\|=22 .$

2. Décrire l’ensemble des points M du plan tels que $\|-5\vec{MA}+8\vec{MB}\|=12 .$

3. Décrire l’ensemble des points M du plan tels que 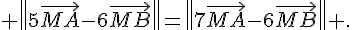$\|5\vec{MA}-6\vec{MB}\|=\|7\vec{MA}-6\vec{MB}\| .$

4. Décrire l’ensemble des points M du plan tels que 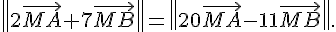$\|2\vec{MA}+7\vec{MB}\|=\|20\vec{MA}-11\vec{MB}\| .$

Exercice 8

Soit R un repère orthonormé du plan .

1. Construire le barycentre G des points {(A,2);(B,3)} sachant que les coordonnees, dans R, de ces points sont A(3;4) et B(-1;2) .

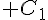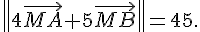2. On note l’ensemble des points M du plan tels que $\|4\vec{MA}+5\vec{MB}\|=45 .$ .

Déterminer l’équation de l’ensemble .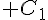

2. On note 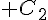l’ensemble des points M du plan tels que $\|3\vec{MA}+2\vec{MB}\|=\|7\vec{MA}-2\vec{MB}\| .$ .

Déterminer l’équation de l’ensemble .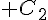

Exercice 9 – Ensemble de points

0. Dans un repère orthonormé 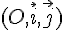$(O,\vec{i},\vec{j})$ du plan,
placer les points A(– 2 ; 0), B(4 ; 0), C(2 ; 4) et D(0 ; 4).

1. Démontrer que ABCD est un trapèze isocèle.

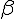2. Déterminer les réels $\alpha$ et $\beta$ tels que O soit le barycentre de (A ; $\alpha$ ) (B ; 1) (C ; 1) (D ; $\beta$ ) .

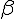3. Soit I le milieu de [BC] et G le point tel que 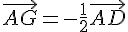$\vec{AG}=-\frac{1}{2}\vec{AD}$ .

a. Déterminer des réels a et b tels que G soit le barycentre de (A ; a) (D ; b).

b. Démontrer que G, O et I sont alignés. Préciser la position de O sur [GI].

4.
a. Déterminer et construire l’ensemble 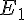des points M du plan tels que

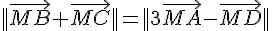$||\vec{MB}+\vec{MC}||=||3\vec{MA}-\vec{MD}||$ .

b. Justifier que O appartient à .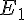

5.
a. Déterminer et construire l’ensemble 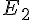Des points M du plan tels que :

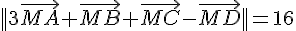
$|| 3\vec{MA}+\vec{MB}+\vec{MC}-\vec{MD} ||=16$

b. Justifier que B et D appartiennent à .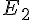

Exercice 10 – Carré et parallélogramme
ABC est un triangle de sens direct.

DBA est un triangle isocèle et rectangle en D de sens direct.

ACE est un triangle isocèle et rectangle en E de sens direct.

On construit le point L tel que 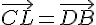$\vec{CL}=\vec{DB}$ .

1. Faire une figure.

2. Démontrer que EDL est un triangle rectangle isocèle en E de sens direct. .

Exercice 11 – Extrait du baccalauréat S sur le barycentre

On considère un triangle ABC du plan .

1.a. Déterminer et construire le point G, barycentre du système de points pondérés :

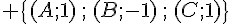$\{(A;1)\,;\,(B;-1)\,;\,(C;1)\}$ .

b. Déterminer et construire le point G’, barycentre du système de points pondérés :

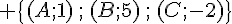$\{(A;1)\,;\,(B;5)\,;\,(C;-2)\}$ .

2.a. Soit J le milieu de [AB].

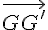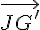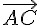Exprimer $\vec{GG'}$ et $\vec{JG'}$ en fonction de $\vec{AB}$ et $\vec{AC}$ et en déduire l’intersection des droites (GG’) et (AB) .

b. Montrer que le barycentre I du système de points pondérés :

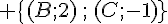$\{(B;2)\,;\,(C;-1)}$ appartient à (GG’) .

3. Soit D un point quelconque du plan et O le milieu de [CD] et K le milieu de [OA] .

a. Déterminer trois réels a, b, c tels que K soit le barycentre du système de points pondérés :

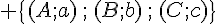$\{(A;a)\,;\,(B;b)\,;\,(C;c)\}$ .

b. Soit X le point d’intersection de (DK) et (AC).

Déterminer les réels a’ et c’ tels que X soit barycentre du système de points pondérés :

$\{(A;a')\,;\,(C;c')\}$ .

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

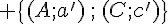Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «barycentre : exercices de maths en terminale corrigés en PDF.» au format PDF.

D'autres fiches dans la section exercices de maths en terminale S

Télécharger nos applications gratuites avec tous les cours et exercices corrigés.

D'autres fiches similaires à barycentre : exercices de maths en terminale corrigés en PDF..

Barycentre : exercices de maths en 1ère corrigés en PDF.
79
Des exercices sur le barycentre en 1ère avec l'utilisation de la définition du barycentre de n points pondérés et des propriétés du barycentre comme l'associativité. Tous ces exercices en première disposent d'un corrigé détaillé afin que les élèves puissent réviser en ligne. Exercice 1 - Barycentre de points pondérés 1.…
Barycentre : corrigé des exercices de maths en 1ère en PDF.
65
Le corrigé des exercices de maths en 1ère sur le barycentre n points pondérés. Utiliser les propriétés de stabilité et d'associativité du barycentre en première. Exercice 1 : A vous d'effectuer ces constructions en sachant que le barycentre est forcément aligné avec les points A et B. Exercice 2 :…
Vecteurs et translation : exercices de maths en 2de corrigés en PDF.
61
Des exercices de maths sur les vecteurs et la translation en classe de 2de. Vous trouverez pour chaque exercice sa correction détaillée en seconde. Exercice 1 - Les point sont-ils alignés Les points P, Q et R sont-ils alignés ? Exercice 2 - Points alignés et vecteurs ABCD est un…

Les dernières fiches mises à jour.

Voici les dernières ressources similaires à barycentre : exercices de maths en terminale corrigés en PDF. mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 13 624 621 cours et exercices de maths téléchargés en PDF.