Bac de maths 2024 en France : sujet et corrigé en terminale.

Le sujet n°1 du bac de maths en France 2024 avec son corrigé pour l’enseignement de spécialité. Un sujet à télécharger en PDF en terminale. L’énoncé porte sur des affirmations vraies ou fausses avec des suites numériques, une équation différentielle et une asymptote horizontale. Des probabilités avec l’étude d’une agence de marketing. De la géométrie dans l’espace avec un vecteur normal à un plan et une équations cartésienne d’un plan mais, également, une représentation paramétrique d’une droite. L’étude d’une fonction contenant un logarithme népérien avec le calcul d’une aire par le biais d’une intégrale. Ce sujet du baccalauréat de maths 2024 en France dispose de sa correction à télécharger.

BACCALAURÉAT GÉNÉRAL
ÉPREUVE D’ENSEIGNEMENT DE SPÉCIALITÉ
FRANCE 2024
MATHÉMATIQUES
Durée de l’épreuve : 4 heures

L’usage de la calculatrice avec mode examen actif est autorisé.
L’usage de la calculatrice sans mémoire « type collège » est autorisé.

Le candidat doit traiter les quatre exercices proposés.
Le candidat est invité à faire figurer sur la copie toute trace de recherche, même
incomplète ou non fructueuse, qu’il aura développée.
La qualité de la rédaction, la clarté et la précision des raisonnements seront prises en
compte dans l’appréciation de la copie. Les traces de recherche, même incomplètes
ou infructueuses, seront valorisées.

Exercice 1 (4 points)
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque
réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.

1. On considère la fonction définie sur $\mathbb{R}$ par : $f(x)=5xe^{-x}$ .
On note la courbe représentative de dans un repère orthonormé.

Affirmation 1 :
L’axe des abscisses est une asymptote horizontale à la courbe .

Affirmation 2 :
La fonction est solution sur $\mathbb{R}$ de l’équation différentielle $(E)\,:\,\,y'+y=5e^{-x}$ .

2. On considère les suites 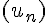, 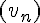et , telles que, pour tout entier naturel :
$u_n\leq\,\,v_n\leq\,\,w_n$ .
De plus, la suite 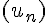converge vers −1 et la suite converge vers 1.

Affirmation 3 :
La suite 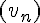converge vers un nombre réel appartenant à l’intervalle [−1; 1].
On suppose de plus que la suite 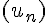est croissante et que la suite est décroissante.

Affirmation 4 :
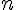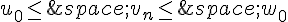Pour tout entier naturel , on a alors : $u_0\leq\,\,v_n\leq\,\,w_0$ .

Exercice 2 (5 points)
Une agence de marketing a étudié la satisfaction des clients concernant le service
clientèle à l’occasion de l’achat d’un téléviseur.

Ces achats ont été réalisés soit sur internet, soit dans une chaîne de magasins d’électroménager, soit dans une enseigne de grandes surfaces.
Les achats sur internet représentent 60 % des ventes, les achats en magasin
d’électroménager 30 % des ventes et ceux en grandes surfaces 10 % des ventes.

Une enquête montre que la proportion des clients satisfaits du service clientèle
est de :

75 % pour les clients sur internet ;
90 % pour les clients en magasin d’électroménager ;
80 % pour les clients en grande surface.

On choisit au hasard un client ayant acheté le modèle de téléviseur concerné.
On définit les événements suivants :

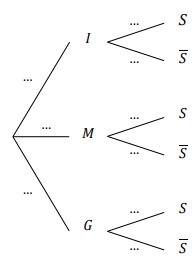
I : « le client a effectué son achat sur internet » ;
M : « le client a effectué son achat en magasin d’électroménager » ;
G : « le client a effectué son achat en grande surface » ;
S : « le client est satisfait du service clientèle ».

Si A est un événement quelconque, on notera 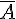$\,\overline{A}$ son événement contraire et 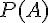sa probabilité.

1. Reproduire et compléter l’arbre ci-dessous.

2. Calculer la probabilité que le client ait réalisé son achat sur internet et soit satisfait du service clientèle.
3. Démontrer que $P(S)\,=\,0,8$ .
4. Un client est satisfait du service clientèle. Quelle est la probabilité qu’il ait effectué son achat sur internet ? On donnera un résultat arrondi à 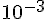$10^{-3}$ près.

5. Pour réaliser l’étude, l’agence doit contacter chaque jour 30 clients parmi les acheteurs du téléviseur. On suppose que le nombre de clients est suffisamment important pour assimiler le choix des 30 clients à un tirage avec remise.

On note 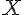la variable aléatoire qui, à chaque échantillon de 30 clients, associe le nombre de clients satisfaits du service clientèle.

a. Justifier que 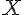suit une loi binomiale dont on précisera les paramètres.

b. Déterminer la probabilité, arrondie à 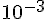$10^{-3}$ près, qu’au moins 25 clients soient satisfaits dans un échantillon de 30 clients contactés sur une même journée.

6. En résolvant une inéquation, déterminer la taille minimale de l’échantillon de
clients à contacter pour que la probabilité qu’au moins l’un d’entre eux ne soit pas
satisfait soit supérieure à 0,99.

7. Dans les deux questions a. et b. qui suivent, on ne s’intéresse qu’aux seuls achats sur internet.
Lorsqu’une commande de téléviseur est passée par un client, on considère que le
temps de livraison du téléviseur est modélisé par une variable aléatoire 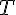égale à
la somme de deux variables aléatoires 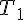et .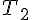
La variable aléatoire 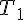modélise le nombre entier de jours pour l’acheminement
du téléviseur depuis un entrepôt de stockage vers une plateforme de distribution.
La variable aléatoire 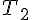modélise le nombre entier de jours pour l’acheminement
du téléviseur depuis cette plateforme jusqu’au domicile du client.

On admet que les variables aléatoires 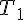et 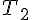sont indépendantes, et on donne :
• L’espérance 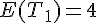et la variance ;
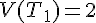• L’espérance 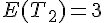et la variance .

a. Déterminer l’espérance et la variance de la variable aléatoire .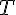
b. Un client passe une commande de téléviseur sur internet. Justifier que la
probabilité qu’il reçoive son téléviseur entre 5 et 9 jours après sa commande
est supérieure ou égale à 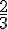$\frac{2}{3}$ .

Exercice 3 (5 points)
L’espace est muni d’un repère orthonormé 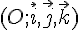$(O;\vec{i},\vec{j},\vec{k})$ .
On considère les points A (5 ; 5 ; 0), B (0 ; 5 ; 0 ), C (0 ; 0 ; 10) et D (0 ; 0 ; $-\frac{5}{2}$ ).

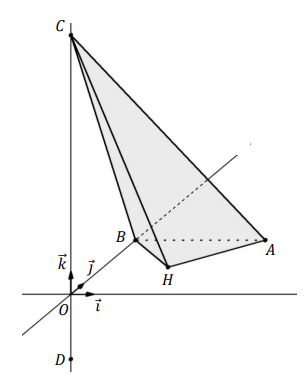
1.
a. Montrer que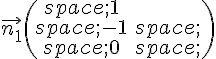 $\vec{n_1}\begin{pmatrix}\,1\\\,-1\,\\\,0\,\end{pmatrix}$ est un vecteur normal au plan .
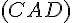b. En déduire que le plan 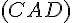a pour équation cartésienne : .
2. On considère la droite 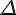$\Delta$ de représentation paramétrique :

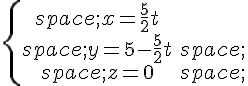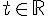$\{\begin{matrix}\,x=\frac{5}{2}t\\\,y=5-\frac{5}{2}t\,\\\,z=0\,\end{matrix}.$ où $t\in\mathbb{R}$ .

a. On admet que la droite 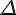$\Delta$ et le plan 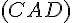sont sécants en un point H.

Justifier que les coordonnées de H sont 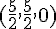$(\frac{5}{2},\frac{5}{2},0)$ .
b. Démontrer que le point H est le projeté orthogonal de B sur le plan .

3.
a. Démontrer que le triangle ABH est rectangle en H.
b. En déduire que l’aire du triangle ABH est égale à $\frac{25}{4}$ .
4.
a. Démontrer que (CO) est la hauteur du tétraèdre ABCH issue de C.
b. En déduire le volume du tétraèdre ABCH.
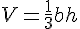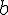On rappelle que le volume d’un tétraèdre est donné par : $V=\frac{1}{3}bh$ où est
l’aire d’une base et la hauteur relative à cette base.
5. On admet que le triangle ABC est rectangle en B.

Déduire des questions précédentes la distance du point H au plan .

Exercice 4 (6 points)
Partie A : étude de la fonction .
La fonction est définie sur l’intervalle $]0;\,+\infty[$ par :

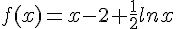$f(x)=x-2+\frac{1}{2}lnx$ , où ln désigne la fonction logarithme népérien.

On admet que la fonction est deux fois dérivable sur $]0;\,+\infty[$ , on note 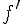sa dérivée et 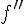sa dérivée seconde.
1.
a. Déterminer, en justifiant, les limites de en 0 et en $+\infty$ .
b. Montrer que pour tout appartenant à $]0;\,+\infty[$ , on a : $f'(x)=\frac{2x+1}{2x}$ .

c. Étudier le sens de variation de sur $]0;\,+\infty[$ .
d. Étudier la convexité de sur $]0;\,+\infty[$ .
2.
a. Montrer que l’équation 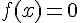admet dans $]0;\,+\infty[$ une solution unique qu’on
notera $\alpha$ et justifier que $\alpha$ appartient à l’intervalle [1 ; 2].
b. Déterminer le signe de 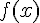pour $x\in]0;\,+\infty[$ .
c. Montrer que $ln(\alpha\,)\,=\,2(2\,-\,\alpha\,)$ .

Partie B : étude de la fonction g.
La fonction 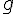est définie sur ]0 ; 1] par $g(x)=-\frac{7}{8}x^2+x-\frac{1}{4}x^2lnx$ .
On admet que la fonction 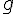est dérivable sur ]0 ; 1] et on note 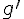sa fonction dérivée.
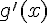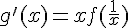1. Calculer pour $x\in\,]0\,;\,1]$ puis vérifier que $g'(x)=xf(\frac{1}{x})$ .
2.
a. Justifier que pour appartenant à l’intervalle $]0;\frac{1}{\alpha\,}[$ , on a $f(\frac{1}{x})>0$ .
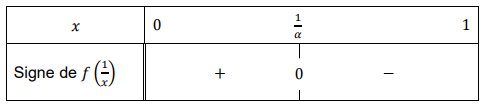
b. On admet le tableau de signes suivant :

En déduire le tableau de variations de 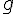sur l’intervalle ]0 ; 1].
Les images et les limites ne sont pas demandées.

Partie C : un calcul d’aire.
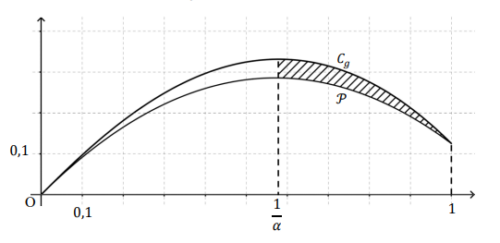
On a représenté sur le graphique ci-dessous :
• La courbe 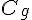de la fonction ;
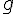• La parabole 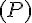d’équation $y=-\frac{7}{8}x^2+x$ sur l’intervalle ]0 ; 1].

On souhaite calculer l’aire 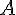du domaine hachuré compris entre les courbes 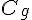et ,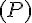
et les droites d’équations 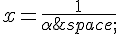$x=\frac{1}{\alpha\,}$ et .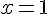
On rappelle que $ln(\alpha\,)\,=\,2(2\,-\,\alpha\,)$ .
1.
a. Justifier la position relative des courbes 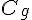et 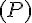sur l’intervalle ]0 ; 1].
b. Démontrer l’égalité :
$\int_{\frac{1}{\alpha\,}}^{1}x^2lnx\,dx=\frac{-\alpha\,^3-6\alpha\,+13}{9\alpha\,^3}$ .
2. En déduire l’expression en fonction de $\alpha$ de l’aire .

Consulter le corrigé

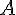Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac de maths 2024 en France : sujet n° 1 et corrigé pour l'enseignement de spécialité.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.