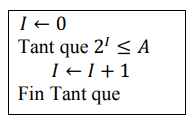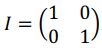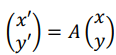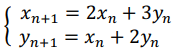Bac s 2019 France : sujet et corrigé à télécharger en PDF

BACCALAURÉAT GÉNÉRAL
SESSION 2019
ÉPREUVE DU VENDREDI 21 JUIN 2019
MATHÉMATIQUES – Série S –
Durée de l’épreuve : 4 heures
L’usage de tout modèle de calculatrice, avec ou sans mode examen, est autorisé.
Enseignement de Spécialité Coefficient : 9
Le sujet est composé de quatre exercices indépendants.

Le candidat doit traiter tous les exercices.
Le candidat est invité à faire figurer sur la copie toute trace de recherche, même incomplète ou non fructueuse, qu’il aura développée.
Il est rappelé que la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l’appréciation des copies.

Exercice 1 (6 points) : commun à tous les candidats
Partie A
On considère la fonction définie sur l’ensemble $\mathbb{R}$ des nombres réels par :

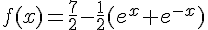$f(x)=\frac{7}{2}-\frac{1}{2}(e^x+e^{-x})$ .
1.
a. Déterminer la limite de la fonction f en +∞.
b. Montrer que la fonction f est strictement décroissante sur l’intervalle [0; +∞[.
c. Montrer que l’équation f(x) = 0 admet, sur l’intervalle [0; +∞[, une unique solution, qu’on note $\alpha$ .
2. En remarquant que, pour tout réel x, f(-x)=f(x), justifier que l’équation f(x)=0 admet exactement deux solutions dans $\mathbb{R}$ et qu’elles sont opposées.

Partie B
Les serres en forme de tunnel sont fréquemment utilisées pour la culture des plantes fragiles ; elles limitent les effets des intempéries ou des variations de température.
Elles sont construites à partir de plusieurs arceaux métalliques identiques qui sont ancrés au sol et supportent une bâche en plastique.
Le plan est rapporté à un repère orthonormé d’unité 1 mètre. La fonction f et le réel $\alpha$ sont définis dans la partie A.

Dans la suite de l’exercice, on modélise un arceau de serre par la courbe 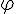$\varphi$ de la fonction f sur l’intervalle $[-,\alpha,;,\alpha]$ .
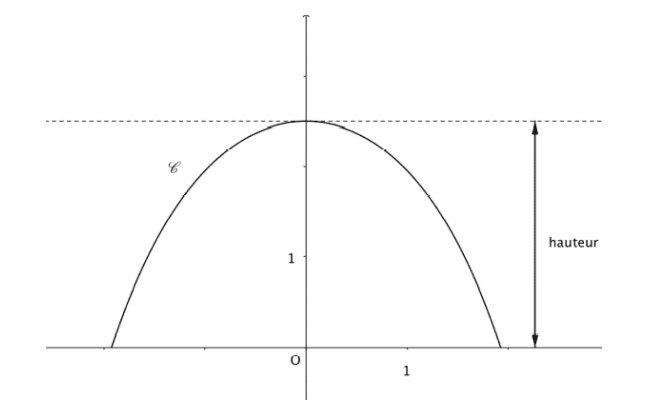
On a représenté ci-dessous la courbe $\varphi$ sur l’intervalle $[-,\alpha,;,\alpha]$ .

On admettra que la courbe $\varphi$ admet l’axe des ordonnées pour axe de symétrie.

1. Calculer la hauteur d’un arceau.
2.
a. Dans cette question, on se propose de calculer la valeur exacte de la longueur de la courbe $\varphi$ sur l’intervalle $[0;\alpha,]$ .

On admet que cette longueur est donnée, en mètre, par l’intégrale :
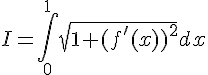$I=\int_{0}^{1}\sqrt{1+(f'(x))^2}dx$ .
Montrer que pour tout réel x, on a : 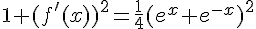$1+(f'(x))^2=\frac{1}{4}(e^x+e^{-x})^2$ .

b. En déduire la valeur de l’intégrale I en fonction de $\alpha$ .
Justifier que la longueur d’un arceau, en mètre, est égale à : 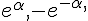$e^\alpha,-e^{-\alpha,}$ .

Partie C
On souhaite construire une serre de jardin en forme de tunnel.
On fixe au sol quatre arceaux métalliques, dont la forme est celle décrite dans la partie précédente, espacés de 1,5 mètre, comme indiqué sur le schéma ci-dessous.
Sur la façade sud, on prévoit une ouverture modélisée sur le schéma par le rectangle ABCD de largeur 1 mètre et de longueur 2 mètres.

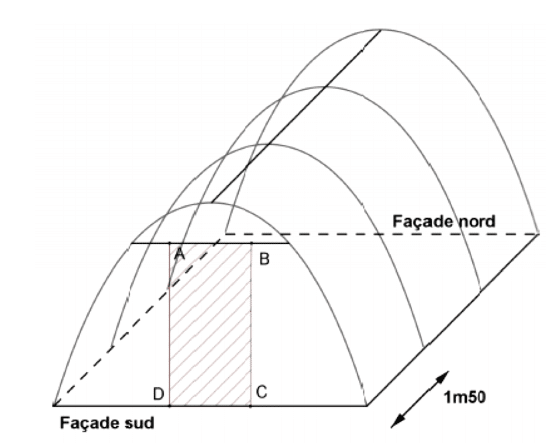
On souhaite connaître la quantité, exprimée en m², de bâche plastique nécessaire pour réaliser cette serre. Cette bâche est constituée de trois parties, l’une recouvrant la façade nord, l’autre la façade sud (sauf l’ouverture), la troisième partie de forme rectangulaire recouvrant le dessus de la serre.

1. Montrer que la quantité de bâche nécessaire pour recouvrir les façades sud et nord est donnée, en m², par :

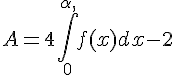$A=4\int_{0}^{\alpha,}f(x)dx-2$ .
2. On prend 1,92 pour valeur approchée de $\alpha$ .

Déterminer, au m² près, l’aire totale de la bâche plastique nécessaire pour réaliser cette serre.

Exercice 2 ( 5 points ) : commun à tous les candidats
Une plateforme informatique propose deux types de jeux vidéo : un jeu de type A et un jeu de type B.

Partie A
Les durées des parties de type A et de type B, exprimées en minutes, peuvent être modélisées respectivement par deux variables aléatoires notées 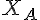et .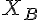
La variable aléatoire 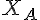suit la loi uniforme sur l’intervalle [9; 25] .
La variable aléatoire 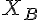suit la loi normale de moyenne 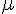$\mu$ et d’écart type 3.

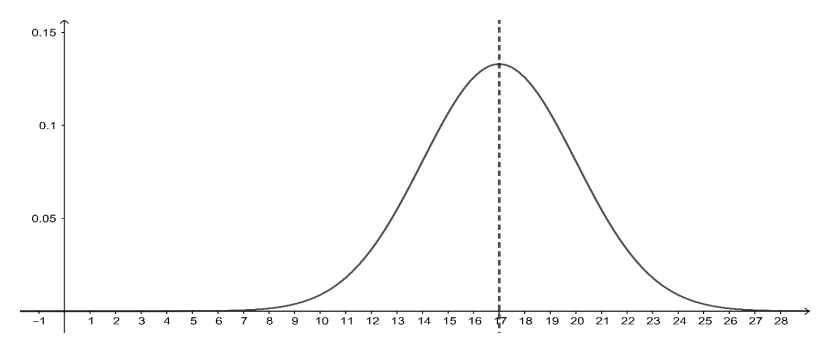
La représentation graphique de la fonction de densité de cette loi normale et son axe de symétrie sont donnés ci-dessous.

1.
a. Calculer la durée moyenne d’une partie de type A.
b. Préciser à l’aide du graphique la durée moyenne d’une partie de type B.
2.
On choisit au hasard, de manière équiprobable, un type de jeu. Quelle est la probabilité que la durée d’une partie soit inférieure à 20 minutes ? On donnera le résultat arrondi au centième.

Partie B
On admet que, dès que le joueur achève une partie, la plateforme lui propose une nouvelle partie selon le modèle suivant :

– si le joueur achève une partie de type A, la plateforme lui propose de jouer à nouveau une partie de type A avec une probabilité de 0,8 ;
– si le joueur achève une partie de type B, la plateforme lui propose de jouer à nouveau une partie de type B avec une probabilité de 0,7.

Pour tout entier naturel supérieur ou égal à 1, on note 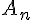et 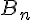les événements :
L : « la n-ième partie est une partie de type A. »
L : « la n-ième partie est une partie de type B. »
Pour tout entier naturel n supérieur ou égal à 1, on note 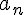la probabilité de l’événement .
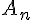1.
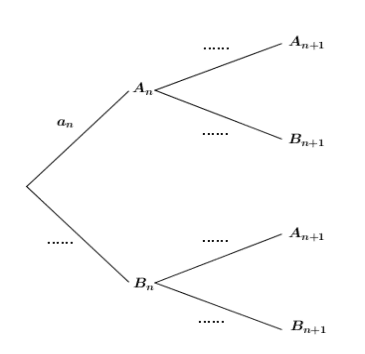
a. Recopier et compléter l’arbre pondéré ci-dessous.

b. Montrer que pour tout entier naturel 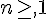$n\geq\,,1$ , on a :
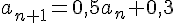$a_{n+1}=0,5a_n+0,3$ .
Dans la suite de l’exercice, on note 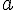la probabilité que le joueur joue au jeu A lors de sa première partie, où 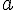est un nombre réel appartenant à l’intervalle [0; 1]. La suite ( 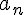) est donc définie par :
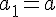, et pour tout entier naturel ≥ 1, LP* = 0,5L + 0,3.

2. Étude d’un cas particulier :

Dans cette question, on suppose que a= 0,5.
a. Montrer par récurrence que pour tout entier naturel 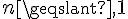$n\geq\,,1$ , on a : 0 ≤ 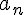≤ 0,6.
b. Montrer que la suite (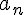) est croissante.
c. Montrer que la suite (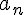) est convergente et préciser sa limite.

3. Étude du cas général :

Dans cette question, le réel appartient 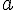à l’intervalle [0; 1].

On considère la suite (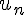 ) définie pour tout entier naturel ≥ 1 par : 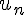= 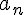− 0,6.
a. Montrer que la suite (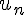) est une suite géométrique.
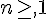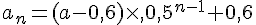b. En déduire que pour tout entier naturel $n\geq\,,1$ , on a : $a_n=(a-0,6)\times ,0,5^{n-1}+0,6$ .
c. Déterminer la limite de la suite (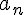). Cette limite dépend-elle de la valeur de ?
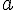d. La plateforme diffuse une publicité insérée en début des parties de type A et une autre publicité insérée en début des parties de type B.

Quelle devrait être la publicité la plus vue par un joueur s’adonnant intensivement aux jeux vidéo ?

Exercice 3 ( 4 points ) : commun à tous les candidats
Les quatre questions de cet exercice sont indépendantes.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.

Une réponse non justifiée n’est pas prise en compte.

Une absence de réponse n’est pas pénalisée.
1. Dans l’ensemble C des nombres complexes, on considère l’équation (E) ∶ 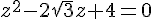$z^2-2\sqrt{3}z+4=0$ .

On note A et B les points du plan dont les affixes sont les solutions de (E).

Affirmation 1 :

Le triangle OAB est équilatéral.
2. On note le nombre complexe : 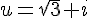$u=\sqrt{3}+i$ et on note 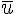$\overline{u}$ son conjugué.
Affirmation 2 :

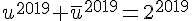$u^{2019}+\overline{u}^{2019}=2^{2019}$ .

3. Soit un entier naturel non nul.

On considère la fonction définie sur l’intervalle [0; +∞[ par :
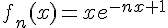
$f_n(x)=xe^{-nx+1}$

Affirmation 3 :

Pour tout entier naturel n ≥ 1, la fonction admet un maximum.
4. On note 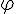$\varphi$ la courbe représentative de la fonction f définie sur $\mathbb{R}$ par :

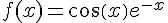$f(x)=cos(x)e^{-x}$ .

Affirmation 4 :

La courbe 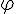$\varphi$ admet une asymptote en +∞.

5. Soit A un nombre réel strictement positif.

On considère l’algorithme ci- dessous.

On suppose que la variable I contient la valeur 15 en fin d’exécution de cet algorithme.

Affirmation 5:

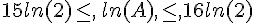
$15ln(2)\leq\,,\,ln(A),\leq\,,16ln(2)$

Exercice 4 ( 5 points ) : pour les candidats ayant suivi l’enseignement de spécialité

On note 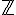$\mathbb{Z}$ l’ensemble des entiers relatifs.
Dans cet exercice, on étudie l’ensemble des matrices qui s’écrivent sous la forme 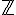, où a, b, c et d appartiennent à l’ensemble $\mathbb{Z}$ et vérifient : .

On note la matrice I identité .

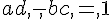Partie A : Quelques exemples de matrices appartenant à l’ensemble
1. Vérifier que la matrice 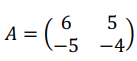appartient à l’ensemble S .
2. Montrer qu’il existe exactement quatre matrices de la forme 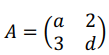appartenant à l’ensemble S ; les expliciter.
3.a. Résoudre dans Z l’équation (E) ∶ 5x − 2y = 1. On pourra remarquer que le couple (1; 2) est une
solution particulière de cette équation.
b. En déduire qu’il existe une infinité de matrices de la forme qui appartiennent à
l’ensemble . Décrire ces matrices.

Partie B : Quelques propriétés des matrices appartenant à l’ensemble
Dans cette partie, on note une matrice appartenant à l’ensemble S.

On rappelle que a, b, c et d sont des nombres entiers relatifs tels que .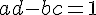
1. Montrer que les entiers a et b sont premiers entre eux.
2. Soit B la matrice :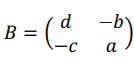
a. Calculer le produit AB. On admet que l’on a AB = BA .
b. En déduire que la matrice A est inversible et donner sa matrice inverse 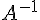$A^{-1}$ .
c. Montrer que la matrice 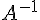$A^{-1}$ appartient à l’ensemble S.
3. Soient x et y deux entiers relatifs.

On note x’ et y’ les entiers relatifs tels que :

.
a. Montrerque x=dx’-by’.

On admet de même que y=ay’- cx’.
b. On note D le PGCD de x et y et on note D’ le PGCD de x’ et y’. Montrer que D=D’.
4.

On considère les suites d’entiers naturels (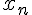) et (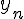) définies par : 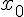= 2019, 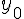= 673 et pour tout entier naturel :

En utilisant la question précédente, déterminer, pour tout entier naturel , le PGCD des entiers 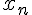et .

Consulter le corrigé en ligne

Vous pouvez télécharger le sujet du bac S de maths 2019 en France métropolitaine au format PDF.

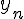Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac s 2019 France : sujet et corrigé à télécharger en PDF» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 142 cours et exercices de maths téléchargés en PDF.