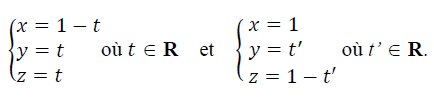Bac Maths 2021: Sujet pour réviser le baccalauréat en PDF.

BACCALAURÉAT GÉNÉRAL
SESSION 2020
MATHÉMATIQUES
Série S
Enseignement Obligatoire – Coefficient 7
Durée de l’épreuve : 4 heures

Exercice n°1 (5 points)
Commun à tous les candidats
Cet exercice est un questionnaire à choix multiples constitué de cinq questions indépendantes.
Pour chaque question, une seule des réponses est exacte. Le candidat portera sur sa copie, sans justification, le numéro de la question et la lettre correspondant à la réponse choisie.
Il sera attribué 1 point si la réponse est exacte, 0 sinon.
1. Une urne contient 5 boules rouges et 3 boules blanches indiscernables au toucher.
On extrait une boule de l’urne et on note sa couleur.
On répète 4 fois cette expérience, de manière indépendante, en remettant la boule à chaque fois dans l’urne.
La probabilité, arrondie au centième, d’obtenir au moins 1 boule blanche est :
Réponse A : 0,15 Réponse B : 0,63 Réponse C : 0,5 Réponse D : 0,85.

2. Soit n étant un entier naturel supérieur ou égal à 2.
Un sac contient n pièces indiscernables au toucher. Ces pièces comportent toutes un côté « PILE » et un côté « FACE » sauf une qui contient deux côtés « FACE ».
On choisit au hasard une pièce du sac puis on la lance.
La probabilité d’obtenir le côté « FACE » est égale à :

Réponse A : $\frac{n-1}{n}$ Réponse B : $\frac{n+1}{2n}$ Réponse C : $\frac{1}{2}$ Réponse D : $\frac{n-1}{2n}$ .

3. On considère T la variable aléatoire suivant la loi normale d’espérance = 60 et d’écart-type = 6.
La probabilité $P_{(T>60)}(T>72)$ arrondie au millième est :
Réponse A : 0,954 Réponse B : 1 Réponse C : 0,023 Réponse D : 0,046.

4. La durée de fonctionnement, exprimée en années, d’un moteur jusqu’à ce que survienne la première panne est modélisée par une variable aléatoire suivant une loi exponentielle de paramètre λ où λ est un réel strictement positif.
La probabilité que le moteur fonctionne sans panne pendant plus de 3 ans est égale à :

Réponse A : $e^{-3\lambda,}$ Réponse B : $1-e^{-3\lambda,}$ Réponse C : $e^{3\lambda,}-1$ Réponse D : $e^{3\lambda,}$ .

5. On note X une variable aléatoire suivant la loi uniforme sur $[0;\frac{\pi}{2}]$ .

La probabilité qu’une valeur prise par la variable aléatoire X soit solution de l’inéquation $cos\,x>\frac{1}{2}$ est égale à :
Réponse A : $\frac{2}{3}$ Réponse B : $\frac{1}{3}$ Réponse C : $\frac{1}{2}$ Réponse D : $\frac{1}{\pi}$ .

Exercice n°2 (4 points)
Commun à tous les candidats
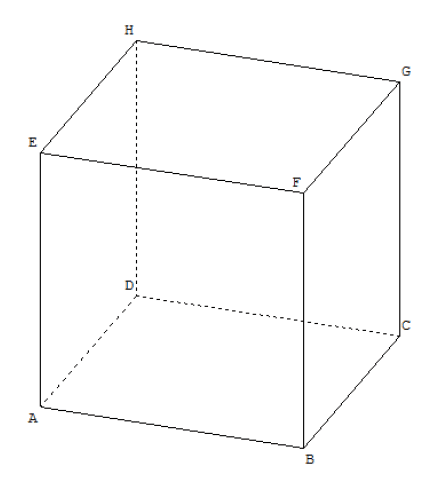
Soit ABCDEFGH un cube. L’espace est rapporté au repère orthonormé $(A,\vec{AB},\vec{AD},\vec{AE})$ .

Pour tout réel t, on considère le point M de coordonnées (1-t ; t ; t ).
1. Montrer que pour tout réel t, le point M appartient à la droite (BH).
On admet que les droites (BH) et (FC) ont respectivement pour représentation paramétrique :

2. Montrer que les droites (BH) et (FC) sont orthogonales et non coplanaires.
3. Pour tout réel ′, on considère le point M′(1 ; t’ ; 1- t’ ).
a. Montrer que pour tous réels et ′, $MM'^2=3(t-\frac{1}{3})^2+2(t'-\frac{1}{2})^2+\frac{1}{6}$ .
b. Pour quelles valeurs de et de ′ la distance MM′ est-elle minimale ? Justifier.
4. On nomme P le point de coordonnées $(\frac{2}{3};\frac{1}{3};\frac{1}{3})$ et Q celui de coordonnées $(1;\frac{1}{2};\frac{1}{2})$ .
Justifier que la droite (PQ) est perpendiculaire aux deux droites (BH) et (FC).

Exercice n°3 (6 points)
Commun à tous les candidats
On considère la fonction définie sur $\mathbb{R}$ par $f(x)=xe^{-x^2+1}$ .

On note $(\varphi,)$ la courbe représentative de dans un repère orthonormé $(O,\vec{i},\vec{j})$ .
1. a. Montrer que pour tout réel, $f(x)=\frac{e}{x}\times ,\frac{x^2}{e^{x^2}}$ .
b. En déduire la limite de f(x) lorsque tend vers $+\infty$ .
2. Pour tout réel x, on considère les points M et N de la courbe $(\varphi,)$ d’abscisses respectives x et – x.
a. Montrer que le point O est le milieu du segment [MN].
b. Que peut-on en déduire pour la courbe $(\varphi,)$ ?
3. Étudier les variations de la fonction sur l’intervalle [0; $+\infty$ [.
4. a. Montrer que l’équation (x)= 0,5 admet sur [0; $+\infty$ [ exactement deux solutions notées $\alpha$ et $\beta$ (avec < $\beta$ ).
b. En déduire les solutions sur [0; $+\infty$ [ de l’inéquation $f(x)\geq\,,0,5$ .
c. Donner une valeur approchée à $10^{-2}$ près de $\alpha$ et $\beta$ .
5. Soit un réel strictement positif. On pose $I_A=\int_{0}^{A}f(x)dx$ .
a. Justifier que $I_A=\frac{1}{2}(e-e^{-A^2+1})$ .
b. Calculer la limite de lorsque tend vers $+\infty$ .
On admet que cette limite est l’aire en unités d’aire située entre la partie de la courbe $(\varphi,)$ sur [0; $+\infty$ [ et l’axe des abscisses.
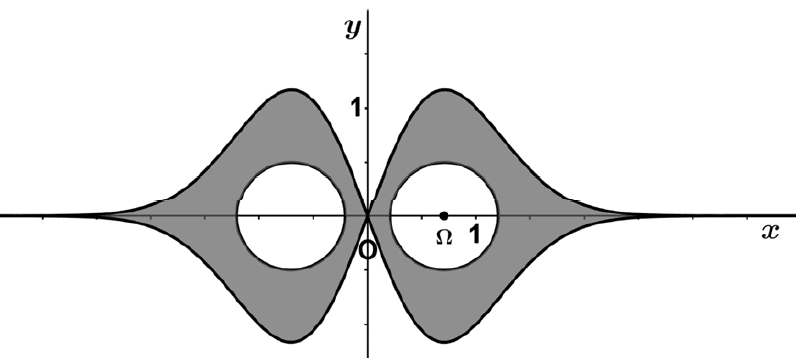
6. Comme illustré sur le graphique ci-dessous, on s’intéresse à la partie grisée du plan qui est délimitée
par :

la courbe $(\varphi,)$ sur $\mathbb{R}$ et la courbe $(\varphi,')$ symétrique de $(\varphi,)$ par rapport à l’axe des abscisses ;
le cercle de centre $\Omega,(\frac{\sqrt{2}}{2};0)$ et de rayon 0,5 et son symétrique par rapport à l’axe des ordonnées.
On admet que le disque de centre $\Omega,(\frac{\sqrt{2}}{2};0)$ et de rayon 0,5 et son symétrique par rapport à l’axe des ordonnées sont situés entièrement entre la courbe $(\varphi,)$ et la courbe $(\varphi,')$ .

Déterminer une valeur approchée en unité d’aire au centième près de l’aire de cette partie grisée du plan.

Exercice n°4 (5 points)
Candidats n’ayant pas suivi l’enseignement de spécialité
Le plan complexe est muni d’un repère orthonormé direct $(O,\vec{u},\vec{v})$ .
On considère la suite de nombres complexes définie par :
et pour tout entier naturel , $z_{n+1}=(1+i)z_n-i$ .
Pour tout entier naturel n, on note le point d’affixe .
On note B le point d’affixe 1.
1.
a. Montrer que et que .
b. Calculer .
c. Sur la copie, placer les points B, A1, A2 et A3 dans le repère orthonormé direct $(O,\vec{u},\vec{v})$ .
d. Démontrer que le triangle BA1A2 est isocèle rectangle.

2. Pour tout entier naturel , on pose .
a. Démontrer que pour tout entier naturel , on a $u_{n+1}=\sqrt{2}u_n$ .
b. Déterminer à partir de quel entier naturel , la distance est strictement supérieure à 1000.

On détaillera la démarche choisie.

3. a. Déterminer la forme exponentielle du nombre complexe 1 + i .
b. Démontrer par récurrence que pour tout entier naturel $z_n=1-(\sqrt{2})^ne^{i\frac{n\pi}{4}}$ .
c. Le point $A_{2020}$ appartient-il à l’axe des abscisses ? Justifier.

Consulter le corrigé en ligne

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac Maths 2021: Sujet blanc pour réviser le baccalauréat de mathématiques» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 151 cours et exercices de maths téléchargés en PDF.