Bac de maths 2024: sujet et corrigé blanc n° 2 en PDF.
Mis à jour le 2 décembre 2025
Un sujet du bac de maths 2024 avec son corrigé afin de réviser en ligne. Ce sujet du baccalauréat porte sur :
- les équations différentielles;
- les intégrales;
- la fonction exponentielle;
- les intégrales;
- les probabilités;
- les suites numériques;
- fonctions convexes ou concaves.
Ce sujet est corrigé et permet aux élèves de terminale de réviser en ligne et de se préparer aux épreuves du baccalauréat 2024 en mathématiques.
BACCALAURÉAT GÉNÉRAL
BAC MATHS 2024 -blanc n°2
Durée de l’épreuve : 4 heures
Exercice 1 :
L’exercice est constitué de deux parties indépendantes.
Partie I
On considère l’équation différentielle
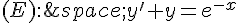
1. Soit la fonction définie sur  par
par 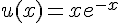 ..
..
Vérifier que la fonction est une solution de l’équation différentielle ().
2. On considère l’équation différentielle (′) ∶ ′ + = 0.
Résoudre l’équation différentielle (′) sur  .
.
3. En déduire toutes les solution de l’équation différentielle () sur  .
.
4. Déterminer l’unique solution de l’équation différentielle () telle que (0) = 2.
Partie II
Dans cette partie, est un nombre réel fixé que l’on cherche à déterminer.
On considère la fonction 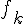 définie sur
définie sur  par
par
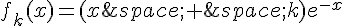
Soit ℎ la fonction définie sur  par
par
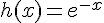
On note 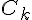 la courbe représentative de la fonction
la courbe représentative de la fonction 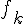 dans un repère orthogonal et la courbe
dans un repère orthogonal et la courbe
représentative de la fonction ℎ.
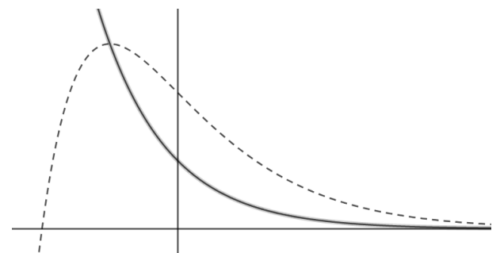
On a représenté sur le graphique en annexe les courbes et sans indiquer les unités sur les axes
ni le nom des courbes.
1. Sur le graphique en annexe à rendre avec la copie, l’une des courbes est en traits pointillés,
l’autre est en trait plein. Laquelle est la courbe ?
2. En expliquant la démarche utilisée, déterminer la valeur du nombre réel et placer sur
l’annexe à rendre avec la copie l’unité sur chacun des axes du graphique.
Annexe :
Exercice 2 :
L’exercice est constitué de deux parties indépendantes.
Partie I
Pour tout entier supérieur ou égal à 1, on désigne par  la fonction définie sur [0 ; 1] par :
la fonction définie sur [0 ; 1] par :
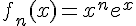
On note  la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère
dans un repère 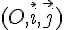 du plan.
du plan.
On désigne par 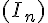 la suite définie pour tout entier supérieur ou égal à 1 par :
la suite définie pour tout entier supérieur ou égal à 1 par :

1. a. On désigne par 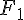 la fonction définie sur [0 ; 1] par :
la fonction définie sur [0 ; 1] par :

Vérifier que 1 est une primitive de la fonction 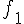 .
.
b. Calculer 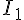 .
.
2. À l’aide d’une intégration par parties, établir la relation pour tout supérieur ou égal à 1,
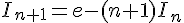
3. Calculer 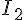 .
.
4. On considère la fonction mystère écrite dans le langage Python :

À l’aide des questions précédentes, expliquer ce que renvoie l’appel mystere(5).
Partie II
1. Sur le graphique ci-dessous, on a représenté les courbes 1, 2, 3, 10, 20 et 30 .
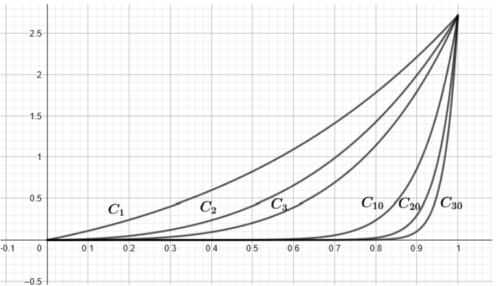
a. Donner une interprétation graphique de 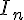 .
.
b. Quelle conjecture peut-on émettre sur la limite de la suite (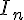 ) ?
) ?
2. Montrer que pour tout 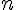 supérieur ou égal à 1,
supérieur ou égal à 1,
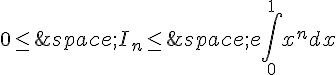
3. En déduire 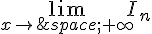 .
.
Exercice 3 :
Dans un examen, une épreuve notée sur dix points est constituée de deux exercices : le premier est
noté sur deux points, le deuxième sur huit points.
Partie I
Le premier exercice est constitué de deux questions Q1 et Q2.
Chaque question est notée sur un point. Une réponse correcte rapporte un point ; une réponse
incorrecte, incomplète ou une absence de réponse rapporte zéro point.
On considère que :
- Un candidat pris au hasard a une probabilité 0,8 de répondre correctement à la question Q1.
- Si le candidat répond correctement à Q1, il a une probabilité 0,6 de répondre correctement à
Q2 ; s’il ne répond pas correctement à Q1, il a une probabilité 0,1 de répondre correctement
à Q2.
On prend un candidat au hasard et on note :
- l’événement : « le candidat répond correctement à la question Q1 » ;
- l’événement : « le candidat répond correctement à la question Q2 ».
On note 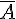 et
et 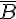 les événements contraires de
les événements contraires de 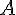 et de
et de  .
.
1. Recopier et compléter les pointillés de l’arbre pondéré ci-dessous.
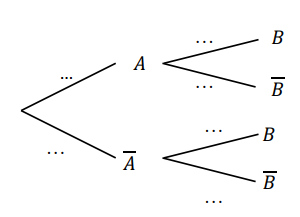
2. Calculer la probabilité que le candidat réponde correctement aux deux questions Q1 et Q2.
3. Calculer la probabilité que le candidat réponde correctement à la question Q2.
On note :
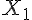 la variable aléatoire qui, à un candidat, associe sa note à la question Q1 ;
la variable aléatoire qui, à un candidat, associe sa note à la question Q1 ; la variable aléatoire qui, à un candidat, associe sa note à la question Q2 ;
la variable aléatoire qui, à un candidat, associe sa note à la question Q2 ;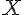 la variable aléatoire qui, à un candidat, associe sa note à l’exercice, c’est-à-dire
la variable aléatoire qui, à un candidat, associe sa note à l’exercice, c’est-à-dire
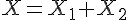 .
.
4. Déterminer l’espérance de 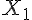 et de
et de  .
.
En déduire l’espérance de 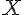 .
.
Donner une interprétation de l’espérance de 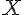 dans le contexte de l’exercice.
dans le contexte de l’exercice.
5. On souhaite déterminer la variance de 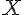 .
.
a. Déterminer 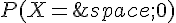 et
et 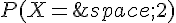 . En déduire
. En déduire 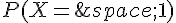 .
.
b. Montrer que la variance de 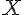 vaut 0,57.
vaut 0,57.
c. A-t-on 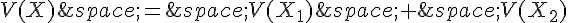 ? Est-ce surprenant ?
? Est-ce surprenant ?
Partie II
Le deuxième exercice est constitué de huit questions indépendantes.
Chaque question est notée sur un point. Une réponse correcte rapporte un point ; une réponse
incorrecte et une absence de réponse rapporte zéro point.
Les huit questions sont de même difficulté : pour chacune des questions, un candidat a une
probabilité 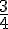 de répondre correctement, indépendamment des autres questions.
de répondre correctement, indépendamment des autres questions.
On note 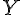 la variable aléatoire qui, à un candidat, associe sa note au deuxième exercice, c’est-à-dire
la variable aléatoire qui, à un candidat, associe sa note au deuxième exercice, c’est-à-dire
le nombre de bonnes réponses.
1. Justifier que 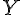 suit une loi binomiale dont on précisera les paramètres.
suit une loi binomiale dont on précisera les paramètres.
2. Donner la valeur exacte de 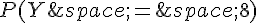 .
.
3. Donner l’espérance et la variance de 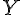 .
.
Partie III
On suppose que les deux variables aléatoires 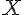 et
et 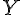 sont indépendantes.
sont indépendantes.
On note la variable aléatoire qui, à un candidat, associe sa note totale à l’examen : 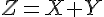 .
.
1. Calculer l’espérance et la variance de 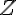 .
.
2. Soit 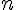 un nombre entier strictement positif.
un nombre entier strictement positif.
Pour entier variant de 1 à 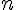 , on note
, on note 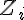 la variable aléatoire qui, à un échantillon de
la variable aléatoire qui, à un échantillon de
élèves, associe la note de l’élève numéro à l’examen.
On admet que les variables aléatoires 1, 2, … , sont identiques à et indépendantes.
On note la variable aléatoire qui, à un échantillon de élèves, associe la moyenne de
leurs notes, c’est-à-dire
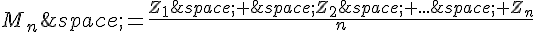
a. Quelle est l’espérance de 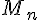 ?
?
b. Quelles sont les valeurs de 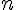 telles que l’écart type de
telles que l’écart type de 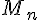 soit inférieur ou égal à 0,5 ?
soit inférieur ou égal à 0,5 ?
c. Pour les valeurs trouvées en b., montrer que la probabilité que 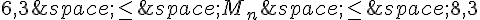 est
est
supérieure ou égale à 0,75.
Exercice 4 :
Cet exercice est un questionnaire à choix multiples.
Pour chaque question, une seule des quatre propositions est exacte. Indiquer sur la copie le numéro
de la question et la lettre de la proposition choisie.
Aucune justification n’est demandée.
Pour chaque question, une réponse exacte rapporte un point. Une réponse fausse, une réponse
multiple ou l’absence de réponse ne rapporte ni n’enlève de point.
Les questions sont indépendantes.
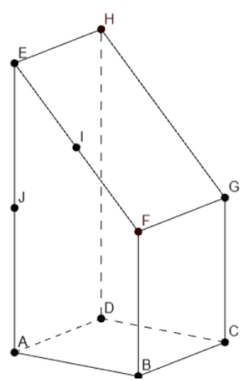
On considère le prisme droit ABFEDCGH tel que AB = AD.
Sa base ABFE est un trapèze rectangle en A, vérifiant 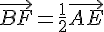 .
.
On note I le milieu du segment [EF].
On note J le milieu du segment [AE].
On associe à ce prisme le repère orthonormé 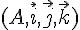 tel que :
tel que :
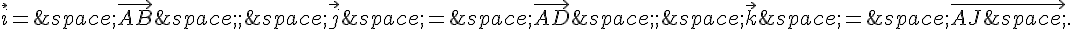
Lequel est un vecteur normal au plan (ABG)?
2. Parmi les droites suivantes, laquelle est parallèle à la droite (IJ) ?
a. (DG) b. (BD) c. (AG) d. (FG)
3. Quels vecteurs forment une base de l’espace ?
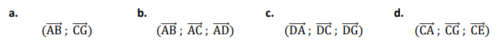
4. Une décomposition du vecteur 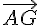 comme somme de plusieurs vecteurs deux à deux
comme somme de plusieurs vecteurs deux à deux
orthogonaux est :
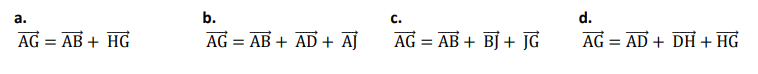
5. Le volume du prisme droit ABFEDCGH, est égal à :

Exercice 5 :
Cet exercice est un questionnaire à choix multiples.
Pour chaque question, une seule des quatre propositions est exacte. Indiquer sur la copie le numéro
de la question et la lettre de la proposition choisie.
Aucune justification n’est demandée.
Pour chaque question, une réponse exacte rapporte un point. Une réponse fausse, une réponse
multiple ou l’absence de réponse ne rapporte ni n’enlève de point.
Les questions sont indépendantes.
1. Sur l’intervalle ![[0;2\pi]](https://mathovore.fr/latex-images/a8229b509bc5c7c18bfcff682ca113e8.png) , l’équation sin() = 0,1 admet :
, l’équation sin() = 0,1 admet :
a. zéro solution b. une solution c. deux solutions d. quatre solutions
2. On considère la fonction  définie sur l’intervalle
définie sur l’intervalle ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png) par
par 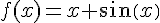 .
.
On admet que  est deux fois dérivable.
est deux fois dérivable.
a. La fonction  est convexe sur l’intervalle
est convexe sur l’intervalle ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png)
b. La fonction  est concave sur l’intervalle
est concave sur l’intervalle ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png)
c. La fonction admet sur l’intervalle ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png) un unique point d’inflexion
un unique point d’inflexion
d. La fonction admet sur l’intervalle ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png) exactement deux points d’inflexion.
exactement deux points d’inflexion.
3. Une urne contient cinquante boules numérotées de 1 à 50. On tire successivement trois
boules dans cette urne, sans remise. On appelle « tirage » la liste non ordonnée des numéros
des trois boules tirées.
Quel est le nombre de tirages possibles, sans tenir compte de l’ordre des numéros?
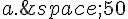
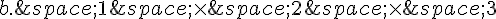
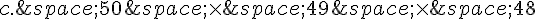
d.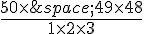
4. On effectue dix lancers d’une pièce de monnaie.
Le résultat d’un lancer est « pile » ou « face ». On note la liste ordonnée des dix résultats.
Quel est le nombre de listes ordonnées possibles ?

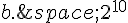
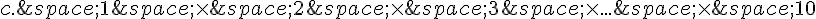
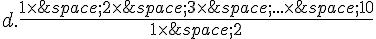
5. On effectue 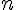 lancers d’une pièce de monnaie équilibrée.
lancers d’une pièce de monnaie équilibrée.
Le résultat d’un lancer est « pile » ou « face ».
On considère la liste ordonnée des 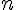 résultats.
résultats.
Quelle est la probabilité d’obtenir au plus deux fois « pile » dans cette liste ?
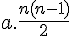

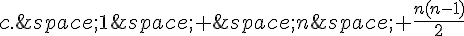
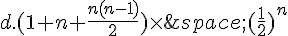
Exercice 6 :
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
Chaque réponse doit être justifiée.
Une réponse non justifiée ne rapporte aucun point.
On considère la suite () définie :
Affirmation 2 : « Pour tout entier naturel , 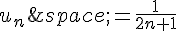 .»
.»
Affirmation 3 : « La suite numérique 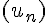 est minorée par
est minorée par 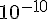 .»
.»
Exercice 7 :
On considère les fonctions 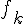 définies sur
définies sur  par
par 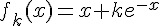 , où
, où 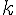 est un réel strictement
est un réel strictement
positif.
1. On s’intéresse dans cette question au cas où 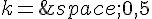 , donc à la fonction
, donc à la fonction  définie sur
définie sur  par
par
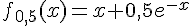 .
.
a. Montrer que la dérivée de  notée
notée  vérifie
vérifie 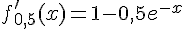 .
.
b. Montrer que la fonction  admet un minimum en
admet un minimum en 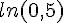 .
.
Soit 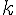 un réel strictement positif.
un réel strictement positif.
On donne le tableau de variations de la fonction 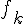 .
.
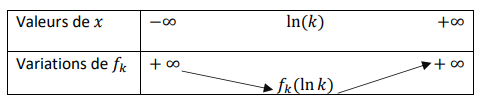
2. Montrer que pour tout réel positif 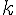 ,
,  .
.
On note 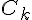 la courbe représentative de la fonction
la courbe représentative de la fonction 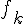 dans un plan muni d’un repère orthonormé.
dans un plan muni d’un repère orthonormé.
On note 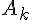 le point de la courbe
le point de la courbe 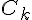 d’abscisse
d’abscisse 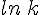 .
.
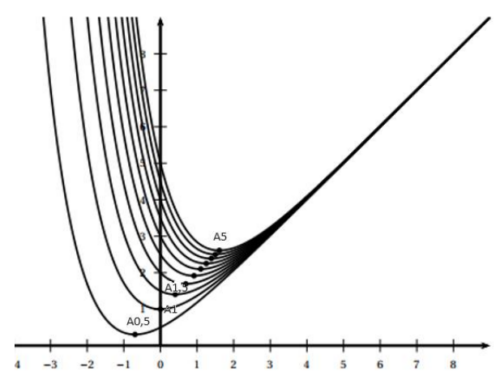
On a représenté ci-dessous quelques courbes 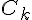 pour différentes valeurs de
pour différentes valeurs de 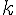 .
.
Une réponse non justifiée ne rapporte aucun point.
Affirmation : « Pour tout réel 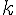 strictement positif, les points
strictement positif, les points 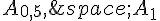 et
et 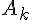 sont alignés. »
sont alignés. »
Exercice 8:
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
Chaque réponse doit être justifiée.
Une réponse non justifiée ne rapporte aucun point.
On considère la suite (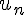 ) définie par
) définie par 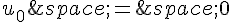 et
et 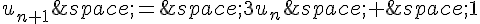 pour tout entier naturel
pour tout entier naturel 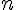 .
.
1. On considère la fonction calcul écrite dans le langage Python qui renvoie la valeur de 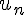 .
.

On considère par ailleurs la fonction liste écrite dans le langage Python :

Affirmation 1 : « l’appel liste(6) renvoie la liste [0, 1, 4, 13, 42, 121]. »
2. Affirmation 2 : « pour tout entier naturel 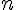 ,
,  . »
. »
3. Affirmation 3 : « pour tout entier naturel 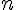 ,
, 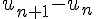 est une puissance de 3. »
est une puissance de 3. »
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «bac de maths 2024: sujet et corrigé blanc n° 2 en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



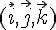 .
.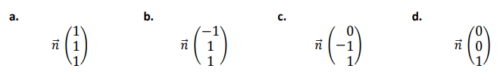
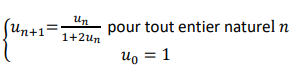
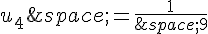 .»
.»