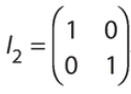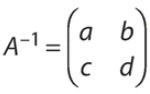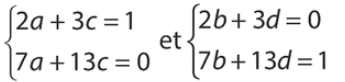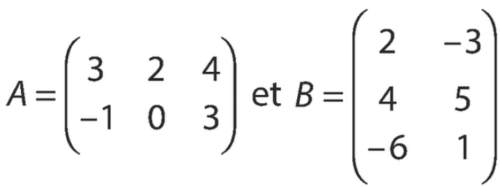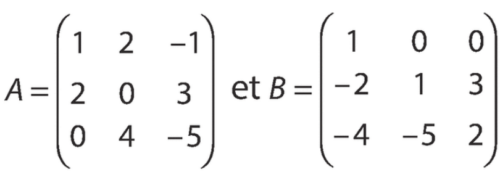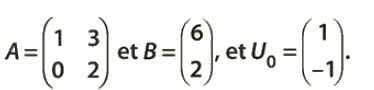Matrices : exercices en terminale spécialité de maths corrigés en PDF.

Exercice 1 – Puissance de matrices
Soit la matrice .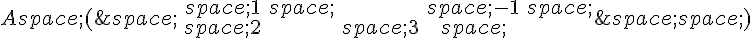

Calculer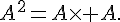 

Exercice 2 – Somme et produit de matrices
Soient les matrices suivantes :

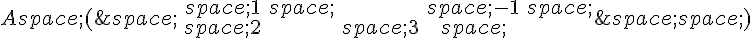et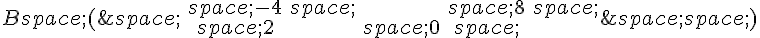

1. Calculer la somme des matrices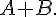 

2. Calculer le produit de matrices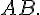 

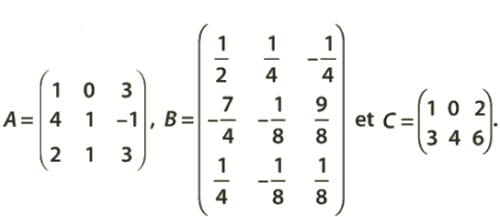
Exercice 3 – Calcul d’un produit
Soient les matrices suivantes :

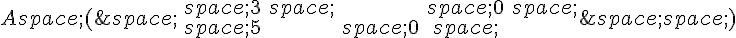et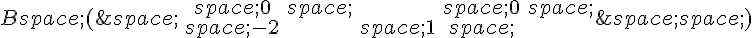

Calculer le produit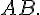 

Exercice 4 :

1. Résoudre les systèmes suivants.

Nous allons voir comment déterminer les solutions de ces systèmes par calcul matriciel.
A. Représentation du système :
1. Déterminer deux matrices et B de dimension telles que 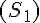équivaut à .
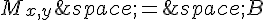2. Donner deux matrices A et X, de dimensions respectives 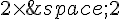et , telles que .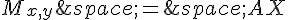
3. En déduire que résoudre le système 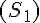revient à résoudre l’équation AX= B, d’inconnue X.

B. Inverse de matrice et résolution matricielle
1. Dans l’équation 2x= 5, pourquoi multiplier les deux membres par 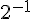permet d’isoler ?
La matrice identité est :

On cherche à déterminer s’il existe une matrice :

telle que .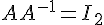

2. Montrer que trouver 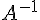revient à résoudre les systèmes :

3. Résoudre ces systèmes et en déduire A-1 (mettre les coefficients sous forme de fraction).
4. Exprimer les coefficients de 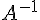 en fonction de ceux de A.
En déduire une formule afin de déterminer la matrice inverse d’une matrice.
5. Multiplier à gauche les deux membres de AX = B par .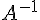

Retrouve-t-on les solutions de   ?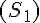
6. De même, mettre le système 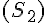sous la forme matricielle .

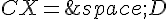Peut-on trouver 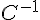? Pourquoi ?

Exercice 5 :

Soient les matrices suivantes :

Calculer AB.

Exercice 6 :

Soient les matrices A et B suivantes :

Calculer le produit AB.

Exercice 7 :

Soit .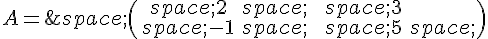

Montrer que A est inversible et déterminer .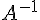

Exercice 8 :

Soient les matrices suivantes :

Montrer que B est l’inverse de A et en déduire les solutions de l’équation XA = C.

Exercice 9 :

1.Mettre le système :

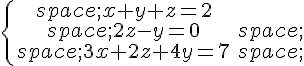
sous forme d’équation matricielle en justifiant.

2. En déduire les solutions du système.

Exercice 10 :

1.Mettre le système :

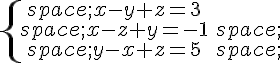
sous forme d’équation matricielle en justifiant.

2. En déduire les solutions du système.

Exercice 11 :

On considère une suite 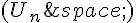de matrices de dimension telle que :

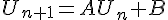
avec

1.Déterminer une matrice X telle que AX + B = X.
2. Soit la suite 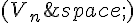définie par 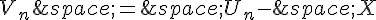pour tout entier n.
Montrer que 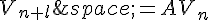pour tout entier n.
En déduire l’expression de 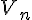, puis de 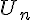en fonction de n et A.

Exercice 12 :

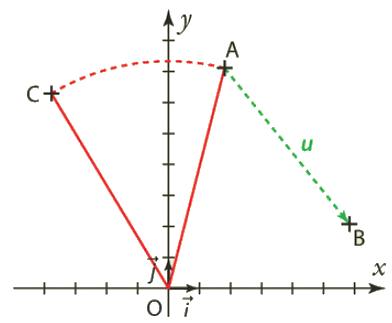
On considère, dans un plan muni d’un repère 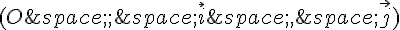, le point .
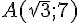1. Soit 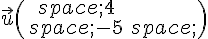, déterminer les coordonnées de B, l’image de A par la translation de vecteur .
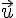2. Donner les coordonnées de C, l’image de A par la rotation de centre O et d’angle .

Exercice 13 :

On  considère, dans un plan muni d’un repère 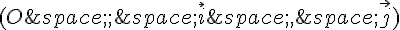le point .
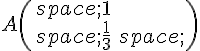1. Soit 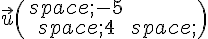, déterminer les coordonnées de B l’image de A par la translation de vecteur .
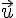2. Donner les coordonnées de C l’image de A par la rotation de centre O et d’angle .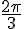

Exercice 14 :

On considère une suite 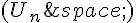de matrices de dimension telle que :

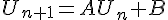
avec

1.Déterminer une matrice X telle que AX + B = X.
2. Soit la suite 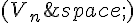définie par 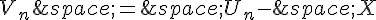pour tout entier n.
Montrer que 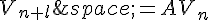pour tout entier n.
3.En déduire l’expression de 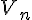, puis de 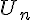en fonction de n et A.

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «matrices : exercices en terminale spécialité de maths corrigés en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

 Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.