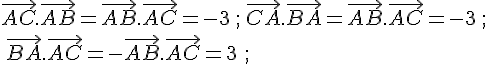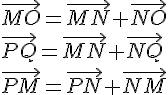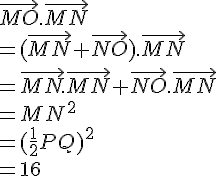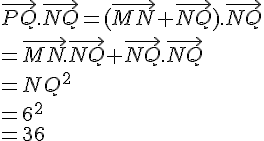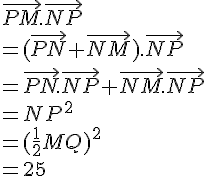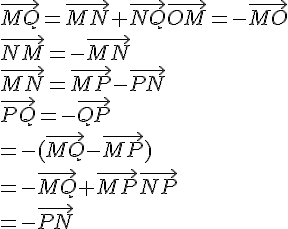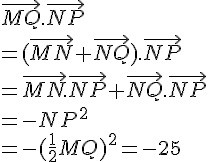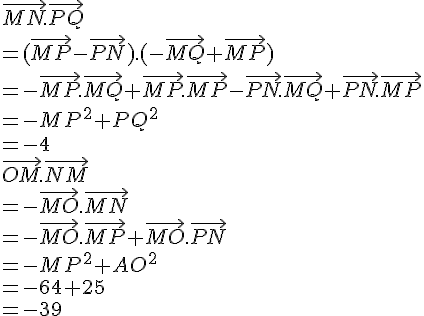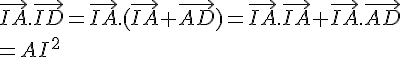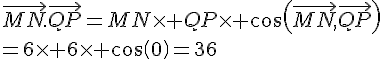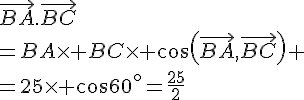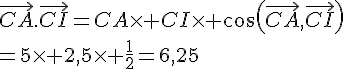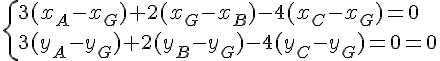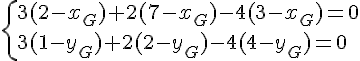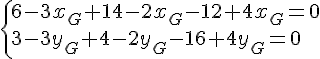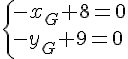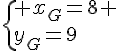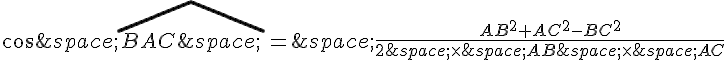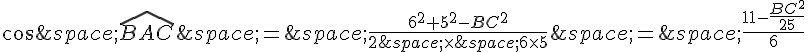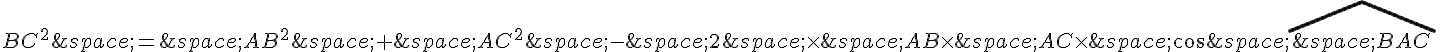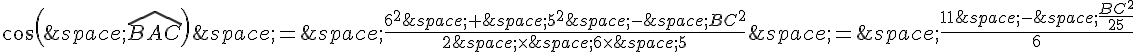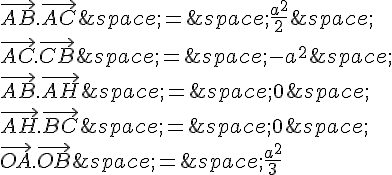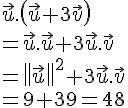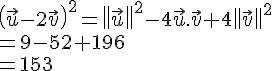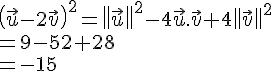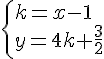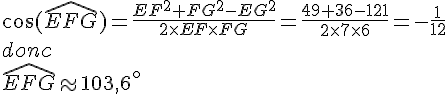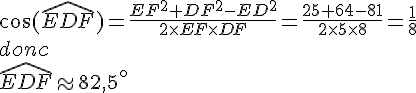Produit scalaire : corrigé des exercices de maths en 1ère en PDF.

Mis à jour le 14 septembre 2025

🔍Corrigés Détaillés

1ere • Scolaire

Produit scalaire

🔎 Analyse : 25 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 1ère en PDF sur le produit scalaire dans le plan. Utiliser les propriétés de bilinéarité du produit scalaire et démontrer que deux vecteurs sont orthogonaux ou colinéaires. Appliquer la relation de Chasles sur les vecteurs en première.

Exercice 1 :

a. AB=3 , AC=5 et $(\vec{AB}.\vec{AC})=-\frac{\pi}{6}+2k\pi$ .
$\vec{AB}.\vec{AC}=AB\times AC \times cos(-\frac{\pi}{6})=15\times \frac{\sqrt{3}}{2}.$

b. AB=1 , AC=4 et $(\vec{AB}.\vec{AC})=-\frac{8\pi}{3}+2k\pi$ .
$\vec{AB}.\vec{AC}=AB\times AC \times cos(\frac{8\pi}{6})=4\times \frac{-1}{2}=-2.$

c. AB=4 , AC=7 et $(\vec{AB}.\vec{AC})=-\frac{\pi}{4}+2k\pi$ .
$\vec{AB}.\vec{AC}=AB\times AC \times cos(\frac{-\pi}{4})=28\times \frac{\sqrt{2}}{2}=14\sqrt{2}.$

d. AB=2 , AC=2 et $(\vec{AB}.\vec{AC})=-\frac{5\pi}{3}+2k\pi$ .
$\vec{AB}.\vec{AC}=AB\times AC \times cos(\frac{5\pi}{3})=4\times \frac{-1}{2}=-2.$

Exercice 2 :

Calculer $\vec{AC}.\vec{AB}\,;\,\vec{CA}.\vec{BA}\,;\,\vec{BA}.\vec{AC}\,\,;$ sachant que :

a. $\vec{AB}.\vec{AC}=-3$
$\vec{AC}.\vec{AB}=\vec{AB}.\vec{AC}=-3\,;\,\vec{CA}.\vec{BA}=\vec{AB}.\vec{AC}=-3\,;\\\,\vec{BA}.\vec{AC}=-\vec{AB}.\vec{AC}=3\,\,;$

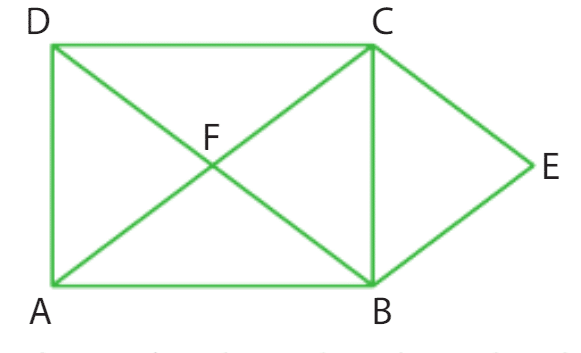
Exercice 3 :

a. On a les vecteurs suivants :

$\vec{MO} = \vec{MN} + \vec{NO} \\\vec{PQ} = \vec{MN} + \vec{NQ} \\ \vec{PM} = \vec{PN} + \vec{NM}$

On peut alors calculer les produits scalaires demandés :

$\vec{MO}.\vec{MN} \\= (\vec{MN} + \vec{NO}).\vec{MN}\\ = \vec{MN}.\vec{MN} + \vec{NO}.\vec{MN} \\= MN^2 \\= (\frac{1}{2}PQ)^2 \\= 16$

$\vec{PQ}.\vec{NQ} = (\vec{MN} + \vec{NQ}).\vec{NQ} \\= \vec{MN}.\vec{NQ} + \vec{NQ}.\vec{NQ} \\= NQ^2 \\= 6^2 \\= 36$

$\vec{PM}.\vec{NP} \\= (\vec{PN} + \vec{NM}).\vec{NP} \\= \vec{PN}.\vec{NP} + \vec{NM}.\vec{NP} \\= NP^2 \\= (\frac{1}{2}MQ)^2 \\= 25$

b. On peut calculer les produits scalaires demandés en utilisant les expressions vectorielles suivantes :

$\vec{MQ} = \vec{MN} + \vec{NQ} \vec{OM} = -\vec{MO} \\ \vec{NM} = -\vec{MN} \\\vec{MN} = \vec{MP} - \vec{PN} \\ \vec{PQ} = -\vec{QP} \\= -(\vec{MQ} - \vec{MP})\\ = -\vec{MQ} + \vec{MP} \vec{NP} \\= -\vec{PN}$

Ainsi, on a :

$\vec{MQ}.\vec{NP} \\= (\vec{MN} + \vec{NQ}).\vec{NP} \\= \vec{MN}.\vec{NP} + \vec{NQ}.\vec{NP} \\= -NP^2\\ = -(\frac{1}{2}MQ)^2 = -25$

$\vec{MN}.\vec{PQ} \\= (\vec{MP} - \vec{PN}).(-\vec{MQ} + \vec{MP}) \\= -\vec{MP}.\vec{MQ} + \vec{MP}.\vec{MP} - \vec{PN}.\vec{MQ} + \vec{PN}.\vec{MP} \\= -MP^2 + PQ^2 \\= -4 \\\\\vec{OM}.\vec{NM}\\ = -\vec{MO}.\vec{MN} \\= -\vec{MO}.\vec{MP} + \vec{MO}.\vec{PN} \\= -MP^2 + AO^2 \\= -64 + 25\\ = -39$

où l’on a utilisé les relations trigonométriques dans le triangle rectangle MPO (où PO est l’hypoténuse) pour exprimer MO et MP en fonction de AO et PQ.

Exercice 4 :

Soit ABCD un carré et I un point de [AB].
On note H le projeté orthogonal de A sur [ID].

$\vec{IA}.\vec{ID}=\vec{IA}.(\vec{IA}+\vec{AD})=\vec{IA}.\vec{IA}+\vec{IA}.\vec{AD}\\=AI^2$
$\vec{IA}.\vec{AD}=0$ car (IA) perpendiculaire à (AD).

Exercice 5 :

Soit ABC un triangle équilatéral de côté 1.
Soit H le projeté orthogonal de A sur (BC).

$\vec{BA}.\vec{AC}=1\times 1\times \frac{\sqrt{3}}{2}$
et $\vec{AB}.\vec{AH}=1\times \frac{\sqrt{3}}{2}\times \frac{1}{2}=\frac{\sqrt{3}}{4}$ .

Exercice 6 :

Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.

1. Justifier que : $\vec{CQ}.\vec{PR}=\vec{CQ}.(\vec{AR}-\vec{AP})$ .

$\vec{CQ}.\vec{PR}=\vec{CQ}.(\vec{PA}+\vec{AR})$ ( d’après la relation de Chasles)

$\vec{CQ}.\vec{PR}=\vec{CQ}.(-\vec{AP}+\vec{AR})$

$\vec{CQ}.\vec{PR}=\vec{CQ}.(\vec{AR}-\vec{AP})$

2. En déduire que les droites (CQ) et (PR) sont perpendiculaires.

Indication :

Montrer que $\vec{CQ}.\vec{PR}=0$

Exercice 7 :

On a $\| \vec{u} \|=2$ et $\| \vec{v} \|=3$ et $\vec{u}$ . $\vec{v}$ = -1

1) Calculez $(\vec{u}+\vec{v})^2$ et $\| (\vec{u} -\vec{v})^2 \|$

$(\vec{u}+\vec{v})^2= \| \vec{u} \|^2+ \| \vec{v} \|^2+2\vec{u}.\vec{v}=4+9-2=11$

2) Calculer ( $\vec{u}$ + $\vec{v}$ ) . (2 $\vec{u}$ -3 $\vec{v}$ )

$(\vec{u}+\vec{v}).(2\vec{u}-3\vec{v})=2\vec{u}.\vec{u}-3\vec{u}.\vec{v}+2\vec{v}.\vec{u}-3\vec{v}.\vec{v}$

$\\=2\times 4-3\times (-1)+2\times (-1)-3\times 3^2$

$\\=8+3-2-27$

$\\=-18$

Exercice 8 :

Démontrer que quelque soit le point M du plan, on a l’égalité :

$MA^2-MB^2=(\vec{MA}+\vec{MB}).\vec{BA}=2\vec{MI}.\vec{BA}$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).(\vec{MA}-\vec{MB})$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).(\vec{MA}+\vec{BM})$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).(\vec{BM}+\vec{MA})$

${\color{DarkRed} MA^2-MB^2=(\vec{MA}+\vec{MB}).\vec{BA}}$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).\vec{BA}$

$MA^2-MB^2=(\vec{MI}+\vec{IA}+\vec{MI}+\vec{IB}).\vec{BA}$

$MA^2-MB^2=(2\vec{MI}+\vec{IA}+\vec{IB}).\vec{BA}$

or I est le milieu de [AB] donc $\vec{IA}+\vec{IB}=\vec{0}$

$MA^2-MB^2=(2\vec{MI}+\vec{IA}+\vec{IB}).\vec{BA}$

$MA^2-MB^2=(2\vec{MI}+\vec{0}).\vec{BA}$

$MA^2-MB^2=(2\vec{MI}).\vec{BA}$

${\color{DarkBlue} MA^2-MB^2=2\vec{MI}.\vec{BA}}$

Exercice 9 :

Commençons par noter que $\vec{AF}= \frac{2}{3}\vec{AB}$ implique que $\vec{FB}= \frac{1}{3}\vec{AB}$ .

Puisque E est le milieu de [AD] , alors $\vec{GC}=2\vec{GK}$ implique que $\vec{GK}=\vec{GC}-\vec{GE}=\vec{GC}-\frac{1}{2}\vec{GA}$ .

Et puisque $A, F, K \in (EK)$ (car ils sont également sur (AB) ), alors

$\vec{GK}=\frac{1}{2}\vec{EK}-\frac{1}{2}\vec{GA}=\frac{1}{2}(\vec{EK}-\vec{GA})=\frac{1}{2}\vec{EA}$ .

Soit L le point d’intersection de (MK) et (AC) .

Puisque les diagonales de ABCD se coupent en leur milieu, alors L est également le milieu de [AC] .

Donc $\vec{MA}+\vec{LG}=\vec{MC}$ (la somme des deux vecteurs étant égale à $\vec{MC}$ car M est le milieu de [BE] ).

On peut développer $\vec{MA}$ comme suit : $\vec{MA}=\vec{MB}+\vec{BA}$ .

Or $\vec{BA}=\vec{BF}+\vec{FA}= \vec{AB}-\vec{AF}= \frac{1}{3}\vec{AB}$ , et donc $\vec{MA}=\vec{MB}+\frac{1}{3}\vec{AB}$ .

On peut donc écrire : $\vec{MB}+\frac{1}{3}\vec{AB}+\vec{LG}=\vec{MC}.$

Puisque $\vec{GB}=2\vec{GF}$ , alors $\vec{GF}=\frac{1}{2}\vec{GB}= \frac{1}{2}(\vec{GA}+\vec{AB})$ , donc $\vec{GA}=2\vec{GF}-\vec{AB}= \vec{FB}$ , donc $\vec{GA}= \frac{1}{3}\vec{AB}$ .

Essayons maintenant de développer $\vec{LG}$ .

On peut exprimer $\vec{LC}$ comme suit :

$\vec{LC}=\vec{LA}+\vec{AC}=\vec{LA}+\vec{AG}+\vec{GC}=\vec{LA}+\frac{1}{3}\vec{AB}+2\vec{GK}$ (en utilisant les relations données).

Et donc $\vec{LG}=\vec{LC}-\vec{GC}-\vec{GL}$ , où $\vec{GL}=\vec{GB}+\vec{BL}$ .

Or $\vec{GB}=2\vec{GF}$ , et

$\vec{BL}=\vec{BC}-\vec{CL}=\vec{AB}+\vec{AC}-2\vec{AL}=2\vec{AG}+2\vec{GA}-2\vec{AL}=\frac{4}{3}\vec{GA}-2\vec{AL}$ .

Donc $\vec{GL}=2\vec{GF}+\frac{4}{3}\vec{GA}-2\vec{AL}$ .

On peut maintenant réécrire l’équation $\vec{MB}+\frac{1}{3}\vec{AB}+\vec{LG}=\vec{MC}$ en remplaçant $\vec{LG}$ .

Après quelques simplifications, on obtient :

$\vec{MB}-\vec{AL}+\frac{1}{3}\vec{AB}+2\vec{GF}+\frac{4}{3}\vec{GA}=\vec{MC}$

Or $\vec{MA}=\vec{MB}+\frac{1}{3}\vec{AB}$ , donc $\vec{MB}=\vec{MA}-\frac{1}{3}\vec{AB}$ .

Et $\vec{AL}=\vec{AC}-\vec{CL}=\vec{AC}-\frac{1}{2}\vec{LC}= \vec{AC}-\frac{1}{2}(\vec{LA}+\frac{1}{3}\vec{AB}+2\vec{GK})$

(en utilisant le fait que L est le milieu de [AC] ).

Donc $\vec{MB}-\vec{AL}=\vec{MA}-\frac{1}{3}\vec{AB}-\vec{AC}+\frac{1}{2}(\vec{LA}+ \frac{1}{3}\vec{AB}+2\vec{GK})$ .

On peut réécrire $\vec{MA}-\vec{AC}$ en utilisant les vecteurs suivants :

$\vec{MA}=\vec{EA}+\vec{EM}$ et $\vec{AC}=\vec{EC}-\vec{EA}$ .

En substituant cette expression dans l’équation précédente, on obtient :

$\vec{EM}-\frac{1}{3}\vec{AB}+\frac{1}{2}(\vec{LA}+ \frac{1}{3}\vec{AB}+2\vec{GK})=\vec{MC}-2\vec{GF}-\frac{4}{3}\vec{GA}$

Or $\vec{GK}=\frac{1}{2}\vec{EA}$ , donc $\vec{LA}+\frac{1}{3}\vec{AB}+2\vec{GK}=\frac{1}{2}(2\vec{LA}+ \frac{2}{3}\vec{AB}+\vec{EA})=\frac{1}{2}(\vec{LB}+\vec{AM})$ , et donc $\frac{1}{2}(\vec{LA}+\frac{1}{3}\vec{AB}+2\vec{GK})=\vec{LG}$ .

Donc l’équation ci-dessus peut être réécrite :

$\vec{EM}-\frac{1}{3}\vec{AB}+\vec{LG}=\vec{MC}-2\vec{GF}-\frac{4}{3}\vec{GA}$

Rappelons que $\vec{FB}=\frac{1}{3}\vec{AB}$ , donc en utilisant les relations données on a $\vec{GF} = \frac{1}{2}\vec{FB}$ , donc $\vec{GF} = \frac{1}{6}\vec{AB}$ .

De plus, $\vec{GA}=\frac{1}{3}\vec{AB}$ , donc $\vec{LG}=\frac{1}{2}\vec{EA}=\frac{1}{2}(\vec{AB}+\vec{EF})=\frac{1}{2}(\vec{AB}+\frac{2}{3}\vec{AB})=\frac{5}{6}\vec{AB} .$

On peut maintenant réécrire l’équation précédente en remplaçant $\vec{EM} , \vec{LG}$ , $\vec{GF}$ et $\vec{GA}$ par leurs expressions respectives.

On obtient finalement :

$\vec{EB}+\vec{BM}-\frac{1}{2}\vec{AB}-\frac{1}{3}\vec{AB}-\frac{5}{6}\vec{AB}=\vec{MC}-\frac{1}{3}\vec{AB}$

Or $\vec{EB}+\vec{BM}=\vec{EM}$ , donc on peut réécrire l’équation comme suit :

$\vec{EM}-\frac{11}{6}\vec{AB}=\vec{MC}-\frac{1}{3}\vec{AB}$

En d’autres termes,

$\vec{EC}+\vec{CM}-\vec{EM}+\frac{1}{2}\vec{AB}-\frac{5}{6}\vec{AB}=0$

Mais $\vec{EC}+\vec{CM}=\vec{EM}$ (car M est le milieu de [BE] ), donc on a :

$\vec{EM}-\vec{EM}+\frac{1}{2}\vec{AB}-\frac{5}{6}\vec{AB}=0$

Soit, finalement,

$\vec{EM}=\frac{1}{3}\vec{AB}=\vec{GM}$

Et donc $\vec{GK}=\frac{1}{2}\vec{EA}=2\vec{GM}$ , comme demandé.

Exercice 10 :

On sait que $(IH) \perp (BC )$ , puisque H est le projeté orthogonal de A sur BC .

Soit K le point d’intersection de (HI) et (AJ) .

Nous allons montrer que K est le milieu de [HI], ce qui implique que (HI) est bien perpendiculaire à (AJ) (car les médianes d’un triangle sont concourantes et se coupent en leur point commun).

Puisque I est le milieu de [AB], alors $\vec{IA}=\frac{1}{2}\vec{AB}$ , et donc $\vec{AH}=\vec{IA}-\vec{IH}=\vec{IA}-\vec{IB}$ .

De même, puisque J est le milieu de [AC] , alors $\vec{AJ}=\frac{1}{2}\vec{AC}$ , et donc $\vec{AJ}=\vec{IA}+\vec{IJ}$ .

On peut donc écrire :

$\vec{IH}=\vec{IA}-\vec{AH}=\frac{1}{2}\vec{AB}-\vec{IA}+\vec{IB}=\vec{IB}-\frac{1}{2}\vec{AB}$
et
$\vec{IJ}=\vec{AJ}-\vec{IA}=\frac{1}{2}\vec{AC}-\frac{1}{2}\vec{AB}=\frac{1}{2}(\vec{AC}-\vec{AB})$ .

D’après le théorème de la médiane, on a $\vec{AC}+\vec{AB}=2\vec{AJ}$ , donc

$\vec{AC}-\vec{AB}=2(\vec{AJ}-\vec{AB})=2\vec{IJ}$ .

En substituant ces expressions pour $\vec{IH}$ et $\vec{IJ}$ , on a :

$\vec{IH}+\vec{IJ}=\vec{IB}-\frac{1}{2}\vec{AB}+\frac{1}{2}(\vec{AC}-\vec{AB})=\vec{IB}+\frac{1}{2}\vec{AC}$

Sachant que $\vec{IK}=\frac{1}{2}\vec{IJ}$ , on obtient :

$\vec{HK}=\vec{HI}-\vec{IK}=\vec{IH}+\vec{IJ}-\frac{1}{2}\vec{IJ}=\vec{IB}+\frac{1}{2}\vec{AC}-\frac{1}{2}\vec{IJ}$

$\vec{HK}=\vec{IB}+\frac{1}{4}(\vec{AC}-\vec{AB})=\vec{IB}+\frac{1}{4}\vec{BC}$

Or, comme I est le milieu de [AB] , alors $\vec{IB}=\vec{IA}+\vec{AB}=\vec{AH}+\vec{AB}$ . Donc :

$\vec{HK}=\vec{AH}+\vec{AB}+\frac{1}{4}\vec{BC}=\vec{HA}+\vec{AJ}+\frac{1}{4}\vec{BC}$

En remarquant que $\vec{HA}$ est colinéaire à $\vec{BC}$ (car AH est le projeté orthogonal de A sur BC ), on peut écrire :

$\vec{HK}=\vec{BC}+\vec{AJ}+\frac{1}{4}\vec{BC}=\vec{AJ}+\frac{5}{4}\vec{BC}$

Finalement, puisque J est le milieu de [AC] , alors $\vec{AJ}=\frac{1}{2}\vec{AC}$ , et donc

$\vec{HK}=\frac{1}{2}\vec{AC}+\frac{5}{4}\vec{BC}$ .

Or $\vec{AC}$ et $\vec{BC}$ forment un triangle rectangle en A , donc $\vec{AC}=\sqrt{2}\vec{AH}$ et $\vec{BC}=\sqrt{2}\vec{HB}$ .

Donc :

$\vec{HK}=\frac{\sqrt{2}}{2}\vec{AH}+\frac{5\sqrt{2}}{4}\vec{HB}$

Mais on sait que $\vec{AH}$ (respectivement $\vec{HB}$ ) est colinéaire à $\vec{BC}$ (respectivement $\vec{AC}$ ).

Ainsi, $\vec{AH}$ et $\vec{HB}$ sont orthogonaux, et donc $\vec{HK}$ est également orthogonal à $\vec{BC}$ , ce qui signifie que (HK) est perpendiculaire à (BC) .

Nous avons donc montré que (HI) et (AJ) se croisent en un point K qui est le milieu de (HI) . Par conséquent, (HI) est bien perpendiculaire à (HJ) , comme demandé.

Exercice 11 :

Indication : créer un repère dans le parallélogramme.
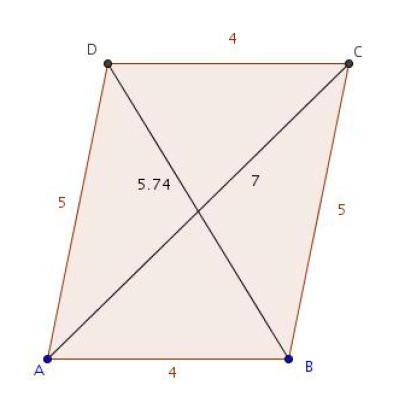
ABCD est un parallélogramme avec AB = 4, AD = 5 et AC = 7.

1.Calculer $\vec{AB}.\vec{AD}$ .

2. En déduire BD.

Exercice 12 :

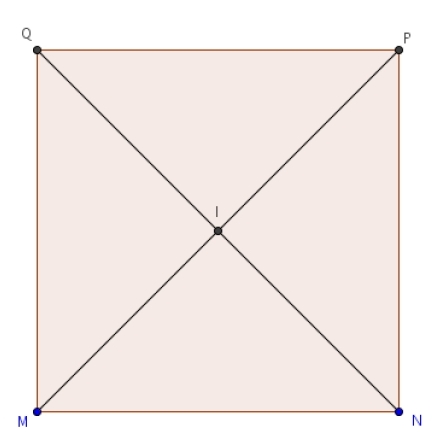
MNPQ est un carré avec MN = 6. I est le centre du carré.

Calculer les produits scalaires suivants :

1. $\vec{MN}.\vec{QP}=MN\times QP\times cos(\vec{MN},\vec{QP})\\=6\times 6\times cos(0)=36$

2. $\vec{MN}.\vec{PN}=MN\times PN\times cos(\vec{MN},\vec{PN})=6\times 6\times cos(90)=0$

3. $\vec{IN}.\vec{IP}=IN\times IP\times cos(\vec{IN},\vec{IP})=3\sqrt{2}\times 3\sqrt{2} \times cos(90)=0$

4. $\vec{QI}.\vec{NI}=QI\times NI\times cos(\vec{QI},\vec{NI})=3\sqrt{2}\times 3\sqrt{2}\times cos(180)=-18$

Exercice 13 :
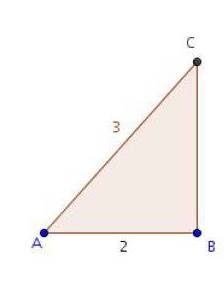
ABC est un triangle dans lequel AB = 2 et AC = 3.

De plus $\vec{AB}.\vec{AC}=4$

Ce triangle est-il rectangle ? Si oui, préciser en quel sommet.

$\vec{AB}.\vec{AC}=AB\times AC\times cos(\vec{AB},\vec{AC})$

$cos(\vec{AB},\vec{AC})=\frac{\vec{AB}.\vec{AC}}{AB\times AC}=\frac{4}{2\times 3}$

$cos(\vec{AB},\vec{AC})=\frac{2}{3}$

Conclusion : le triangle n’est pas rectangle car le cosinus est différent de zéro.

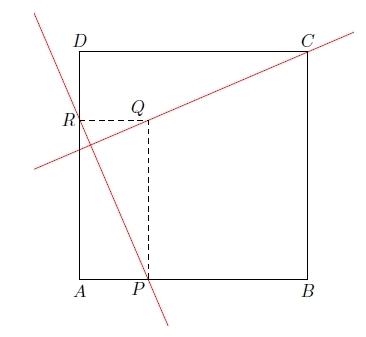
Exercice 14 :

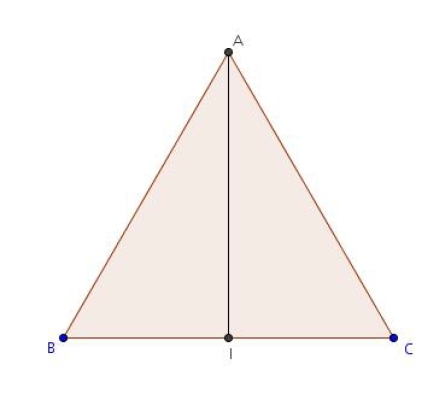
ABC est un triangle équilatéral de côté 5 cm. I est le milieu de [BC].
Calculer les produits scalaires suivants :

1. $\vec{BA}.\vec{BC}$ .

$\vec{BA}.\vec{BC}\\=BA\times BC\times cos(\vec{BA},\vec{BC}) \\=25\times cos60^{\circ}=\frac{25}{2}$

2. $\vec{CA}.\vec{CI}.$

$\vec{CA}.\vec{CI}.$
$\vec{CA}.\vec{CI}=CA\times CI\times cos(\vec{CA},\vec{CI})\\=5\times 2,5\times \frac{1}{2}=6,25$

3. $(\vec{AB}-\vec{AC}).\vec{AI}.$

$(\vec{AB}-\vec{AC}).\vec{AI}=\vec{CB}.\vec{AI}=0$
(Ai) est une médiane mais comme le triangle est équilatéral, c’est aussi une hauteur
donc ces deux vecteurs sont orthogonaux et par conséquent leur produit scalaire nul.

Exercice 15 :

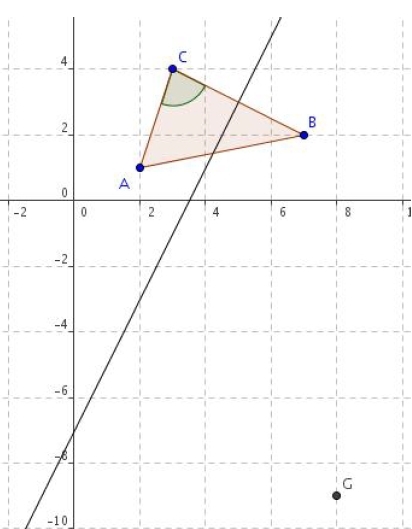
Dans un repère orthonormé $(O;\vec{i},\vec{j})$
on considère les points suivants : A (2 ; 1), B (7 ; 2) et C (3 ; 4).

Toutes les questions suivantes sont indépendantes et sans rapport.

1. Calculer les coordonnées du barycentre G de (A ; 3), (B ; 2) et (C ; – 4).

Tout d’abord, le barycentre existe car $3+2-4=1\neq 0$

$3\vec{GA}+2\vec{GB}-4\vec{GC}=\vec{0}$

$\{ 3(x_A-x_G)+2(x_G-x_B)-4(x_C-x_G)=0 \\3(y_A-y_G)+2(y_B-y_G)-4(y_C-y_G)=0 =0$

$\{ 3(2-x_G)+2(7-x_G)-4(3-x_G)=0 \\3(1-y_G)+2(2-y_G)-4(4-y_G)=0$

$\{ 6-3x_G+14-2x_G-12+4x_G=0 \\3-3y_G+4-2y_G-16+4y_G=0$

$\{ -x_G+8=0 \\-y_G+9=0$

$\{ x_G=8 \\y_G=9$

2. Déterminer une équation cartésienne de la médiatrice de [BC].

un vecteur directeur de [BC] est $\vec{u} (3-7\\4-2 )$

$\vec{u} (-4\\2 )$

$\vec{u} (-2\\1 )$

donc un vecteur normal de la médiatrice est :

$\vec{u} (-2\\1 )$

donc une équation cartésienne est du type :

or le milieu I de [BC] appartient à la médiatrice : 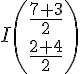$I ( \frac{7+3}{2} \\\frac{2+4}{2} )$ donc $I ( 5 \\3 )$

Nous obtenons :

$-2\times 5+3+c=0$

c=7

Conclusion : une équation cartésienne de la médiatrice est .

3. Calculer $\vec{CB}.\vec{CA}$ .

$\vec{CB}.\vec{CA}= ( 7-3\\2-4 ). ( 2-3\\1-4 )= ( 4\\-2 ). ( -1\\-3 )=4\times (-1)+(-2)\times (-3)=-4+6=2$

4. L’angle $\widehat{C}$ est-il droit ?

Non puisque le produit scalaire n’est pas nul.

Exercice 16 :

1. Dans un triangle ABC , on sait que le carré de la longueur d’un côté est égal à la somme des carrés des longueurs des deux autres côtés, moins deux fois leur produit par le cosinus de l’angle compris entre eux. En utilisant cette formule avec le triangle ABC , on obtient :

$AB^2\,=\,AC^2\,+\,BC^2\,-\,2\times \,AC\times \,BC\times \,\cos\,\widehat{BAC}$

En isolant BC^2 dans cette expression, on a :

$BC^2\,=\,AB^2\,-\,AC^2\,+\,2\,\times \,AC\,\times \,BC\,\times \,\cos\,\widehat{BAC}$

Il nous reste donc à calculer le cosinus de l’angle \angle BAC et le produit $\vec{AB}\cdot\vec{AC}$ :

Tout d’abord, $\vec{AB}\cdot\vec{AC}=\,AB\,\times \,AC\,\times \,cos\,\widehat{BAC}$ . Sachant que AB=6 cm et AC=5 cm (et que $\widehat{BAC}=60^{\circ}\,)$ ,

on obtient :

$\vec{AB}\cdot\vec{AC}\,=\,AB\times \,AC\,\times \,cos\,\widehat{BAC}\,=\,6\,\times \,5\,\times \,\frac{1}{2}\,=\,15\text{\,cm}^2$

Ensuite, on peut utiliser la formule du cosinus dans le triangle ABC :

$cos\,\widehat{BAC\,}=\,\frac{AB^2+AC^2-BC^2}{2\,\times \,AB\,\times \,AC}$

En substituant les valeurs connues, on obtient :

$cos\,\widehat{BAC}\,=\,\frac{6^2+5^2-BC^2}{2\,\times \,6\times 5}\,=\,\frac{11-\frac{BC^2}{25}}{6}$

En multipliant par 6 et en simplifiant, on a :

$6\,\times \,\cos\,\widehat{BAC}\,=\,\frac{55}{30}-\frac{BC^2}{25}$

Finalement, on peut réécrire cette expression de la façon suivante :

$BC^2\,=\,25\,\times \,(\frac{55}{30}-6\,\times \,\cos\,\widehat{BAC})\,=\,25\,\times \,(\frac{11}{3}-2\cos\,\widehat{BAC})$

En substituant la valeur de 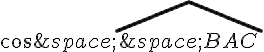$cos\,\widehat{\,BAC}$ obtenue précédemment, on a :

$BC^2\,=\,25\,\times \,(\frac{11}{3}-2\times \,\frac{11-BC^2/25}{6})\,=\,\frac{175}{3}-\frac{10}{3}BC^2$

En résolvant cette équation du second degré pour BC^2 , on obtient :

$BC^2\,=\,\frac{175-3\,\times \,15\,\times \,15}{10}\,=\,50$

Ainsi, $\vec{AB}\cdot\vec{AC}=15\,cm\,^2$ et $BC=5\sqrt{2}$ cm.

2. On peut utiliser la même formule pour le carré d’un côté d’un triangle en fonction des deux autres côtés et de l’angle entre eux.

En isolant BC^2 , on a :

$BC^2\,=\,AB^2\,+\,AC^2\,-\,2\,\times \,AB\times \,AC\times \,cos\,\widehat{\,BAC}$

Il nous faut donc calculer le produit $\vec{AB}\cdot\vec{AC}$ et le cosinus de l’angle $\widehat{BAC}$ .

Tout d’abord, on a $\vec{AB}\cdot\,\vec{AC}=\,AB\times \,AC\times \,cos\,\widehat{BAC}$ .

Sachant que AB=7 cm et AC=4 cm, on obtient :

$\vec{AB}\times \vec{AC}\,=\,AB\,\times \,AC\times \,cos\,\widehat{BAC}\,=\,7\,\times \,4\,\times \,(-\frac{1}{2})\,=\,-14\text{\,cm}^2$

Ensuite, on peut utiliser la formule du cosinus dans le triangle ABC :

$cos\,\widehat{BAC}\,=\,\frac{AB^2+AC^2-BC^2}{2\times \,AB\,\times \,AC}$

En substituant les valeurs connues, on obtient :

$cos\widehat{\,BAC}\,=\,\frac{7^2+4^2-BC^2}{2\times \,7\,\times \,4}\,=\,\frac{33-BC^2}{56}$

On peut donc réécrire la formule pour BC^2 en isolant BC^2 :

$BC^2\,=\,33-56\,\times \,\cos\,\widehat{BAC}\,=\,33-56\,\times \,\frac{33-BC^2}{56}\,=\,2BC^2-33$

Ce qui donne :

$BC^2\,=\,\frac{33}{2}$

Ainsi, $\vec{AB}\cdot\vec{AC}=-14\,cm\,^2$ et $BC=\sqrt{\frac{33}{2}}$ cm.

Exercice 17 :

Il semble y avoir une erreur dans la solution proposée pour le premier cas.

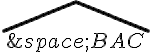
L’équation $BC^2\,=\,AB^2\,-\,AC^2\,+\,2\,\times \,AC\times \,BC\times \,cos(\,\widehat{BAC})$ est en réalité l’équation pour le cosinus de l’angle $\widehat{\,BAC}$ .

Pour isoler BC^2 , on doit utiliser l’équation $BC^2\,=\,AC^2\,+\,AB^2\,-\,2\,\times \,AB\times \,AC\times \,cos(\,\widehat{BAC})$ .

En utilisant cette dernière équation, on trouve :

$\vec{AB}.\vec{AC}\,=\,AB\,\times \,AC\times \,cos(\,\widehat{BAC})\,=\,6\times \,5\times \,\frac{1}{2}\,=\,15$

En utilisant la formule pour le cosinus de l’angle 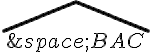$\widehat{\,BAC}$ dans le triangle ABC , on a :

$cos(\,\widehat{BAC})\,=\,\frac{AB^2\,+\,AC^2\,-\,BC^2}{2\,\times \,AB\times \,AC}$

En substituant les valeurs connues, on a :

$cos(\,\widehat{BAC})\,=\,\frac{6^2\,+\,5^2\,-\,BC^2}{2\,\times \,6\times \,5}\,=\,\frac{11\,-\,\frac{BC^2}{25}}{6}$

On peut multiplier les deux membres de cette équation par 6 pour obtenir :

$6\,\times \,cos(\,\widehat{BAC})\,=\,\frac{11}{3}\,-\,\frac{BC^2}{25}$

En isolant BC^2 , on a :

$BC^2\,=\,\frac{175}{3}\,-\,50\,\times \,cos(\,\widehat{BAC})$

En utilisant la valeur précédente du cosinus de l’angle \angle BAC trouvée ci-dessus, on a :

$BC^2\,=\,\frac{175}{3}\,-\,50\,\times \,(\frac{11}{18}\,-\,\frac{BC^2}{75})\,=\,\frac{25\times \,BC^2\,-\,825}{9}$

En résolvant cette équation, on trouve :

BC^2 = \frac{225}{4}

Ainsi, $\vec{AB}.\vec{AC}\,=\,15$ et $BC\,=\,\frac{15}{2}\sqrt{2}$ .

Exercice 18 :

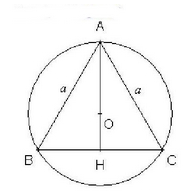
Commençons par tracer la figure :

![Triangle équilatéral ABC avec H le projeté orthogonal de A sur (BC) et O le centre du cercle circonscrit à ABC.]

On a :

– $\vec{AB}$ et $\vec{AC}$ sont deux vecteurs de même norme (égalent à la longueur a d’un côté du triangle). De plus, le triangle ABC étant équilatéral, l’angle $\widehat{BAC}$ vaut $60^{\circ}$ , donc ces vecteurs forment un angle de $60^{\circ}$ l’un avec l’autre. Ainsi, on a :

$\vec{AB}.\vec{AC}\,=\,a^2\,\times \,\cos\,60^{\circ}\,=\,\frac{a^2}{2}$

– On a également $\vec{AC}\,=\,-\vec{CB}$ (vecteur opposé), donc $\vec{AC}.\vec{CB}\,=\,-a^2$ .

– Le vecteur $\vec{AH}$ est le projeté orthogonal de $\vec{AB}$ sur la droite (BC) , donc il est orthogonal à $\vec{BC}$ . Ainsi, $\vec{AB}.\vec{AH}\,=\,0$ $\vec{AB}.\vec{AH}\,=\,0$ .

– Le triangle ABH est rectangle en H , donc l’hypoténuse AH est un diamètre du cercle circonscrit.

Ainsi, le point O (centre du cercle) se situe sur la droite (AH) et le produit scalaire $\vec{AH}.\vec{BC}$ est nul (les vecteurs sont orthogonaux).

– Enfin, le point O étant le centre du cercle circonscrit, les vecteurs $\vec{OA}$ et \vec{OB} ont même norme (le rayon du cercle) et ils font un angle de $60^{\circ}$ l’un avec l’autre (car ils joignent le centre à deux points du cercle qui sont à distance égale). Ainsi,

$\vec{OA}.\vec{OB}\,=\,r^2\,\times \,\cos\,60^{\circ}\,=\,\frac{a^2}{3}$

où r est le rayon du cercle circonscrit (égal à $\frac{a}{\sqrt{3}}$ ).

En résumé, on a :

$\vec{AB}.\vec{AC}\,=\,\frac{a^2}{2}\,\\\\\vec{AC}.\vec{CB}\,=\,-a^2\,\\\\\vec{AB}.\vec{AH}\,=\,0\,\\\\\vec{AH}.\vec{BC}\,=\,0\,\\\\\vec{OA}.\vec{OB}\,=\,\frac{a^2}{3}$

où a est la longueur d’un côté du triangle ABC .

Exercice 19 :

Sachant que les vecteurs $\vec{u}$ et $\vec{v}$ sont tels que $\| \vec{u} \|=3$ , $\| \vec{v} \|=7$ et $\vec{u}.\vec{v} =13$ .

Calculer les produits scalaires suivants :

1. $\vec{u}. (\vec{u}+3\vec{v} )$

$\vec{u}. (\vec{u}+3\vec{v} ) \\=\vec{u}.\vec{u}+3\vec{u}.\vec{v}\\= \| \vec{u} \|^2+3\vec{u}.\vec{v}\\=9+39=48$ $(\vec{u}-2\vec{v} ) ^2= \| \vec{u} \|^2-4\vec{u}.\vec{v}+4 \| \vec{v} \|^2\\=9-52+196\\=153$

2. $(\vec{u}-2\vec{v} ) ^2$

$(\vec{u}-2\vec{v} ) ^2= \| \vec{u} \|^2-4\vec{u}.\vec{v}+4 \| \vec{v} \|^2\\=9-52+28\\=-15$

Exercice 20 :

A quelle condition sur les points A, B et C a-t-on :

$(\vec{AB}+\vec{AC})^2=(AB+AC)^2$

Nous avons :

$(\vec{AB}+\vec{AC})^2=AB^2+AC^2+2\vec{AB}.\vec{AC}=AB^2+AC^2+2AB\times AC\times cos(\vec{AB};\vec{AC})$
et
$(AB+AC)^2=AB^2+AC^3+2\times AB\times AC$

Il faut donc que :

$cos(\vec{AB};\vec{AC})=1$
$(\vec{AB};\vec{AC})=2k\pi$

donc
que le point A appartienne à la droite (BC) privée du segment [BC].

Exercice 21 :
1. $\vec{MA}.\vec{MB}=1.$

Soit I le milieu de [AB] donc isobarycentre de [AB].
$\vec{MA}.\vec{MB}=1$

$(\vec{MI}+\vec{IA} ). (\vec{MI} +\vec{IB} )=1$

en utilisant les propriétés du produit scalaire :

$\vec{MI}.\vec{MI}+\vec{MI}.\vec{IB}+\vec{IA}.\vec{MI}+\vec{IA}.\vec{IB}=1$

$MI^2+\vec{MI}. (\vec{IA}+\vec{IB} )+\vec{IA}.\vec{IB}=1$

$MI^2+\vec{MI}.\vec{0} +\vec{IA}.\vec{IB}=1$

$MI^2+0 +\vec{IA}.\vec{IB}=1$

$MI^2+IA\times IB\times cos\,\pi=1$

$MI^2-IA\times IB=1$

$MI^2=1+IA\times IB$ > 1

$MI^2=1+0,5\times 0,5$

$MI=\sqrt{1,25}$

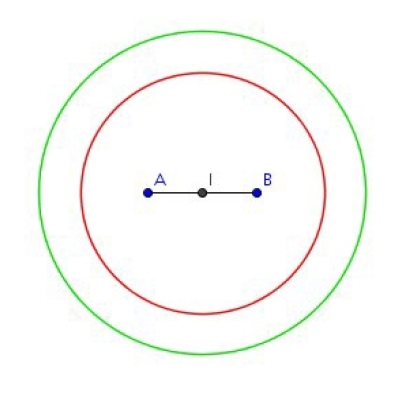
Conclusion : c’est le cercle de centre I et de rayon $\sqrt{1,25}$ dm .

Exercice 22 :

[AB] est un segment de milieu I et AB = 2 cm.

1. Montrer que pour tout point M du plan :

$MA^2-MB^2=2\vec{IM}.\vec{AB}$

Nous avons :

$MA^2-MB^2=(\vec{MA}+\vec{MB}).(\vec{MA}-\vec{MB})$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).(\vec{MA}+\vec{BM})$

$MA^2-MB^2=(\vec{MA}+\vec{MB}).\vec{BA}$

$MA^2-MB^2=(\vec{MI}+\vec{IA}+\vec{MI}+\vec{IB}).\vec{BA}$

$MA^2-MB^2=(2\vec{MI}+\vec{IA}+\vec{IB}).\vec{BA}$

$MA^2-MB^2=2\vec{MI}.\vec{BA}$

car I milieu de [AB] donc $\vec{IA}+\vec{IB}=\vec{0}$

Exercice 23 :

Démontrer que :

1. $\| \vec{u}+\vec{v} \|^2- \| \vec{u}-\vec{v} \|^2=4\vec{u}.\vec{v}$ .

${\color{DarkBlue} \| \vec{u} \|^2+2\vec{u}.\vec{v}+ \| \vec{v} \|^2- \| \vec{u} \|^2+2\vec{u}.\vec{v}- \| \vec{v} \|^2=4\vec{u}.\vec{v}}$

2. $\| \vec{u}+\vec{v} \|^2+ \| \vec{u}-\vec{v} \|^2=2( \|\vec{u} \|^2+ \| \vec{v} \|^2)$ .

3. Quel est le lien avec le losange, le parallélogramme ?

Faire une figure…

4. Démontrer que :

$(\vec{u}+\vec{v}).(\vec{u}-\vec{v})= \| \vec{u} \|^2- \| \vec{v} \|^2$

$(\vec{u}+\vec{v}).(\vec{u}-\vec{v})=\vec{u}.\vec{u}-\vec{u}.\vec{v}+\vec{v}.\vec{u}-\vec{v}.\vec{v}$

$(\vec{u}+\vec{v}).(\vec{u}-\vec{v})=\vec{u}.\vec{u}-\vec{u}.\vec{v}+\vec{u}.\vec{v}-\vec{v}.\vec{v}$ (car le produit scalaire est symétrique)

$(\vec{u}+\vec{v}).(\vec{u}-\vec{v})=\vec{u}.\vec{u}-\vec{v}.\vec{v}$

${\color{DarkBlue} (\vec{u}+\vec{v}).(\vec{u}-\vec{v})= \| \vec{u} \|^2- \| \vec{v} \| ^2}$

5. En déduire qu’un parallélogramme a ses diagonales perpendiculaires si et seulement si ses côtés sont égaux.

Faire une figure….

Exercice 24 :

Indication :

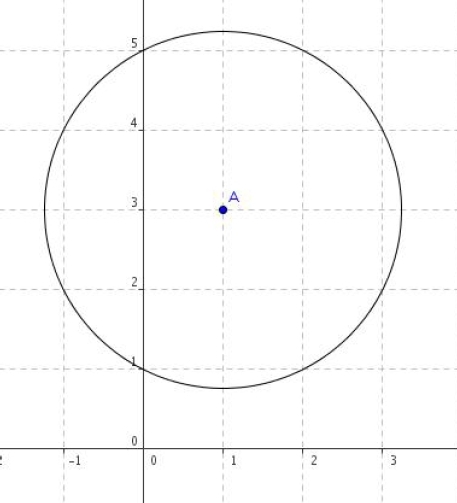
L’équation d’un cercle est

avec $\Omega (x_0;y_0)$ centre du cercle de rayon R.

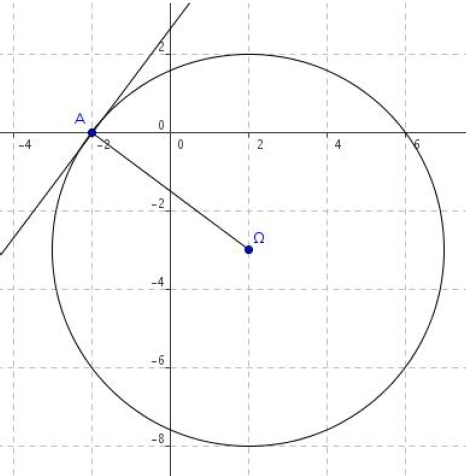
Dans un repère orthonormé $(O;\vec{i},\vec{j})$ , on donne un point $\Omega (2;-3)$ .

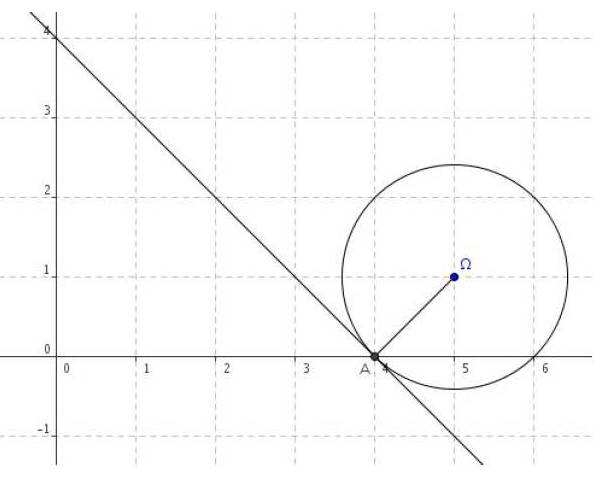
1. Déterminer l’équation du cercle (C) de centre $\Omega$ et de rayon R = 5.

2. Démontrer que le point A( – 2 ; 0) est un point du cercle (C).

3. Déterminer une équation cartésienne de la tangente en A au cercle (C).

Exercice 25 :

Commençons par tracer la figure :

On a :

1. Les vecteurs $\vec{MN}$ et $\vec{QP}$ sont des vecteurs opposés (vecteur directeur de la droite (MN) et vecteur directeur de la droite (PQ) ).

Ainsi, leur produit scalaire est :

$\vec{MN}.\vec{QP} = -MN\cdot QP = -6^2 = -36$

2. Le vecteur $\vec{MN}$ est orthogonal à lui-même (vecteur nul), donc on a :

$\vec{MN}.\vec{PN} = 0$

3. Les vecteurs $\vec{IN}$ et $\vec{IP}$ ont même norme (le rayon du cercle circonscrit au carré) et ils font un angle de $90^{\circ}$ l’un avec l’autre (car ils joignent le centre du carré à deux points du carré qui sont à distance égale). Ainsi,

$\vec{IN}.\vec{IP} = r^2 \times \cos 90^{\circ} = 0$

où r est le rayon du cercle circonscrit au carré (égal à $\frac{MN}{2} = 3$ ).

4. Le point I est le centre du carré, donc les vecteurs $\vec{QI}$ et $\vec{NI}$ sont des vecteurs opposés (ils ont même norme et sont de sens contraire).

Ainsi, leur produit scalaire est :

$\vec{QI}.\vec{NI} = -NI\cdot QI = -r^2 = -3^2 = -9$

où r est le rayon du cercle circonscrit au carré (égal à $\frac{MN}{2} = 3$ ).

Exercice 26 :

On se place dans un repère orthonormé $(O;\vec{i},\vec{j}).$
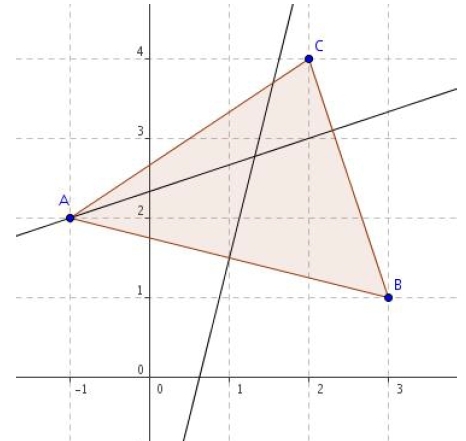
On considère un triangle ABC avec A (- 1 ; 2), B (3 ; 1) et C (2 ; 4).

1. Déterminer une équation de la médiatrice du segment [AB].

Déterminons les coordonnées du vecteur $\vec{AB}$ .

$\vec{AB} ( 3+1\\1-2 )= ( 4\\-1 )$

Déterminons les coordonnées de I milieu du segment [AB] :

$I ( \frac{-1+3}{2}\\\frac{2+1}{2} )= ( 1\\\frac{3}{2} )$

Les coordonnées d’un vecteur directeur de la médiatrice est un vecteur normal au vecteur $\vec{AB}$
donc $\vec{u} ( 1\\4 )$

Tout point M(x,y) appartient à la médiatrice de [AB]

si et seulement si :

$\vec{IM}=k\vec{u}$

(k non nul)

$( x-1\\y-\frac{3}{2} ) = ( k\\4k )$
donc
$\{ k=x-1\\y=4k+\frac{3}{2} .$

$\{ k=x-1\\y=4 (x-1 )+\frac{3}{2} .$

$\{ k=x-1\\y=4x-4+\frac{3}{2} .$

donc l’équation réduite de la médiatrice de [AB] est :

${\color{DarkRed} y=4x-\frac{5}{2}}$

2. Déterminer une équation de la hauteur issue de A dans le triangle ABC.

Déterminons les coordonnées du vecteur $\vec{BC}$ :

$\vec{BC} ( 2-3\\4-1 )= ( -1\\3 )$

Notons H le projeté orthogonal de A sur (BC).

La droite (AH) est donc la hauteur issue du sommet A.

Soit M(x,y) appartient à (AH)

si et seulement si :

$\vec{BC}.\vec{AM}=0$

$( -1\\3 ). (x+1\\y-2 )=0$

$-x +3y-7=0$

3y=x+7

$y=\frac{x+7}{3}$

${\color{DarkRed} y=\frac{1}{3}x+\frac{ 7}{3}}$ est une équation réduite de la hauteur issue de A.

Exercice :

On se place dans un repère orthonormé $(O;\vec{i},\vec{j})$ .

1. Déterminer l’équation du cercle de centre $\Omega (5;1)$ tangent à la droite (D) d’équation :

$x + y - 4 = 0.$

Indication :
on rappelle que la distance entre un point $A(\alpha ;\beta )$ et une droite (D) d’équation ax + by + c = 0 est
donnée par la formule :

$d(A,D)=\frac{ | a\alpha +b\beta +c |}{\sqrt{a^2+b^2}}$

Déterminons la distance entre la tangente et le centre du cercle, ce sera le rayon du cercle.

$d(\Omega ,D)=\frac{ | 1\times 5 +1\times 1 -4 |}{\sqrt{1^2+1^2}}$

$d(\Omega ,D)=\frac{2}{\sqrt{2}}=\frac{2\sqrt{2}}{2}=\sqrt{2}$

L’équation du cercle est :

$(x-5)^2+(y-1)^2=\sqrt{2}^2$

${\color{DarkRed} (x-5)^2+(y-1)^2=2}$

Exercice 27 :
On se place dans un repère orthonormé $(O;\vec{i},\vec{j})$ .

Examiner si les équations suivantes sont des équations de cercle et, le cas échéant, préciser le centre et le rayon du cercle.

1. $x^2 + y^2 - 2x - 6y + 5 = 0.$

C’est un cercle de centre le point I ( 1 ; 3 ) et de rayon $\sqrt{5}$ .

2. $x^2 + y^2 - x - 3y + 3 = 0.$

$(x-\frac{1}{2})^2-\frac{1}{4}+(y-\frac{3}{2})^2+\frac{9}{4}+3=0$

$(x-\frac{1}{2})^2+(y-\frac{3}{2})^2+\frac{8}{4}+\frac{12}{4}=0$

$(x-\frac{1}{2})^2+(y-\frac{3}{2})^2=-5$

Ce n’est pas l’équation d’un cercle .

Exercice 28 :

Indication : utiliser les formule de Pythagore généralisé dans le triangle quelconque.
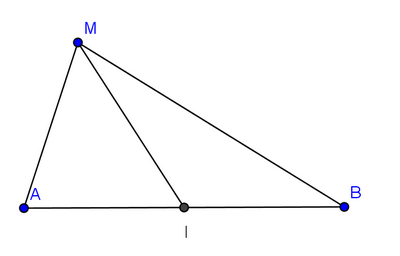
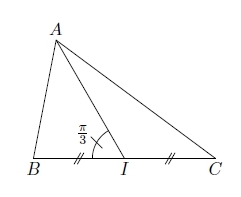
ABC est un triangle et I est le milieu de [BC].
On donne : BC = 4, AI = 3 et $(\vec{IA},\vec{IB})=\frac{\pi}{3}$ .

Calculer :

1. $\vec{AB}.\vec{AC}.$

4. $AB\,et\,AC.$

EXERCICE 29 :

a) Comme O est le centre du carré, on a $\vec{AB}=-\vec{CD}$ et $\vec{AO}=-\vec{OD}$ (les vecteurs ont la même norme mais des directions opposées car ils sont symétriques par rapport à O).
Ainsi, $\vec{AB}.\vec{AO}=-\vec{CD}.\vec{OD}=-CD^2=-8^2=-64$ .

b) Comme O est le centre du carré, $\vec{OB}=-\vec{OA}$ et $\vec{OD}=-\vec{OC}$ (les vecteurs ont la même norme mais des directions opposées car ils sont symétriques par rapport à O).
Ainsi, $\vec{OB}.\vec{OD}=-\vec{OA}.\vec{OC}=-OA^2=-4^2=-16$ .

c) Les vecteurs $\vec{AB}$ et $\vec{AD}$ sont adjacents et forment un angle droit car ils sont des côtés du carré. Ainsi, leur produit scalaire est nul : $\vec{AB}.\vec{AD}=0$ .

d) Les vecteurs $\vec{BO}$ et $\vec{BC}$ sont adjacents et forment un angle droit car ils sont des côtés du carré. Ainsi, leur produit scalaire est nul : $\vec{BO}.\vec{BC}=0$ .

EXERCICE 30 :

On utilise la formule du produit scalaire en coordonnées :

$\vec{u}.\vec{v}=u_1v_1+u_2v_2+u_3v_3$

Comme l’angle entre $\vec{u}$ et $\vec{v}$ vaut 60 degrés, on a $cos(60^{\circ})=\frac{\vec{u}.\vec{v}}{\|\vec{u}\|\|\vec{v}\|}$ ce qui donne :

$\vec{u}.\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos(60^{\circ})=2\times 3\times \frac{1}{2}=3$ .

EXERCICE 31 :

On utilise la formule du produit scalaire en coordonnées :

$\vec{u}.\vec{v}=u_1v_1+u_2v_2+u_3v_3$

Et on sait que $\|\vec{u}\|=6 et \|\vec{v}\|=2$ donc $\vec{u}.\vec{u}=6^2=36$ et $\vec{v}.\vec{v}=2^2=4$ .
On a également $\vec{u}.\vec{v}=-6$ .

En combinant ces informations, on obtient :

$\cos(\theta)=\frac{\vec{u}.\vec{v}}{\|\vec{u}\|\|\vec{v}\|}=\frac{-6}{6\times 2}=-\frac{1}{2}$

L’angle cherché est donc $\theta=\arccos(-\frac{1}{2})=120^{\circ}$ .

EXERCICE 32 :

a) $\vec{u}.\vec{v}=u_1v_1+u_2v_2=(-2)\times (-1)+3\times (-5)=13$

b) $(4\vec{u}).\vec{v}=4(u_1v_1+u_2v_2)=4\times 13=52$

c) $(\vec{u}-\vec{v}).(\vec{u}+\vec{v})=\vec{u}.\vec{u}-\vec{v}.\vec{v}=||\vec{u}||^2-||\vec{v}||^2=4^2-(-5)^2=-9$

EXERCICE 33 :

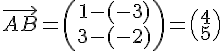
Le vecteur $\vec{AB}$ est donné par $\vec{AB}=\begin{pmatrix}1-(-3)\\3-(-2)\end{pmatrix}=\begin{pmatrix}4\\5\end{pmatrix}$ .

Le produit scalaire entre $\vec{AB}$ et $\vec{u}$ est donné par :

$\vec{AB}.\vec{u}=4\times (-5)+5\times 4=-20+20=0$ .

Comme le produit scalaire est nul, cela signifie que les vecteurs $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

EXERCICE 34 :

a) On utilise la propriété distributive du produit scalaire : $\vec{AB}.\vec{CD} = ( \vec{AB} + \vec{BA} ).( \vec{DC} + \vec{CD} ) = \vec{BA}.\vec{DC} + \vec{AB}.\vec{CD}$ , d’où $\vec{AB}.\vec{CD} = \vec{BA}.\vec{DC}$ .

b) On utilise la relation de Chasles : $\vec{ED} = \vec{EA} + \vec{AB} + \vec{BC} + \vec{CD}$ , d’où $\vec{AB}.\vec{ED} = \vec{AB}.\vec{EA} + \vec{AB}.\vec{AB} + \vec{AB}.\vec{BC} + \vec{AB}.\vec{CD}$ .

Or $\vec{AB}.\vec{EA} = \vec{AB}.\vec{EC}$

car $\vec{EA} = \vec{ED}+\vec{DC}+\vec{CE}, \vec{AB}.\vec{AB} = \|\vec{AB}\|^2$ ,

$\vec{AB}.\vec{BC} = \vec{AC}.\vec{BC} - \vec{AC}.\vec{AB} = 0$ car $\vec{AC}$ et $\vec{AB}$ sont orthogonaux et $\vec{AC}.\vec{BC} = 0$ car ils sont adjacents et forment un angle droit.

Ainsi, on a

$\vec{AB}.\vec{ED} = \vec{AB}.\vec{EC} + \|\vec{AB}\|^2 + \vec{AB}.\vec{CD} = \vec{AB}.\vec{AC} + \vec{AB}.\vec{EC} + \vec{AB}.\vec{CD} + \|\vec{AB}\|^2 = \vec{AB}.\vec{AC} + \vec{AB}.\vec{EC}$ ,

d’où $\vec{AB}.\vec{AC} + \vec{AB}.\vec{EC} = \vec{AB}.\vec{ED}$ .

c) On utilise la relation de Chasles : $\vec{AC} = \vec{AB} + \vec{BC}$ , d’où $\vec{AB}.\vec{AC} = \vec{AB}.\vec{AB} + \vec{AB}.\vec{BC} = \|\vec{AB}\|^2$ . On sait également que $\vec{AB}.\vec{BA} = -\|\vec{AB}\|^2$ car les vecteurs sont opposés.

En combinant ces éléments, on obtient $\vec{AB}.\vec{AC} = \vec{AB}^2 - \vec{BA}.\vec{BC}$ .

EXERCICE 35 :

On utilise la relation de Chasles : $\vec{MD} = \vec{MC} + \vec{CD}$ , d’où $\vec{MC}.\vec{MD} = \vec{MC}$ .

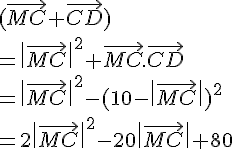
$(\vec{MC}+\vec{CD}) \\\\= \|\vec{MC}\|^2+\vec{MC}.\vec{CD} \\\\= \|\vec{MC}\|^2 - (10-\|\vec{MC}\|)^2\\\\ = 2\|\vec{MC}\|^2-20\|\vec{MC}\|+80$ .

Cette expression est de la forme .

Le coefficient a est strictement positif, donc la fonction est une parabole ouverte vers le haut. Son minimum est atteint en $x= -\frac{b}{2a}= \frac{10}{4} = 2,5$ .

Ainsi, l’ensemble des points M vérifiant $\vec{MC}.\vec{MD}=-9$ est donc le cercle de centre H et de rayon 2,5.

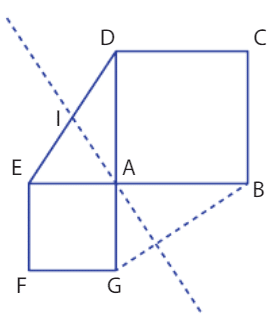
EXERCICE 36 :

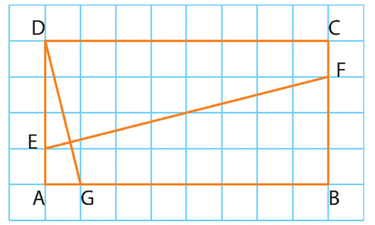
1. Dans le repère (A ; G,E), les coordonnées des vecteurs sont $\vec{AE} =\begin{pmatrix}2\\0\end{pmatrix}, \vec{AG} =\begin{pmatrix}1\\0\end{pmatrix}, \vec{CE} =\begin{pmatrix}-2\\4\end{pmatrix}, \vec{CF} =\begin{pmatrix}-2\\1\end{pmatrix}, \vec{DE} =\begin{pmatrix}0\\4\end{pmatrix}, \vec{DF} =\begin{pmatrix}0\\1\end{pmatrix})$

, et les coordonnées des points sont $A=(0,0), B=(8,0), C=(8,4), D=(0,4), E=(2,0), F=(6,1), G=(1,0)$ .

2. Le vecteur $\vec{EF}$ est donné par $\vec{EF} = \vec{CF} - \vec{CE} =\begin{pmatrix}0\\-3\end{pmatrix}$ .

Le vecteur $\vec{DG}$ est donné par $\vec{AB} - \vec{AD} - \vec{DG} = \begin{pmatrix}8\\0\end{pmatrix} - \begin{pmatrix}0\\4\end{pmatrix} - \vec{DG} =\begin{pmatrix}8\\-4\end{pmatrix} - \vec{DG}$ , d’où $\vec{DG} =\begin{pmatrix}-2\\4\end{pmatrix}$ .

Ainsi, $\vec{EF}.\vec{DG} = 0\times (-2) + (-3)\times 4 = -12$ .

3. Le produit scalaire $\vec{EF}.\vec{DG}$ est négatif, ce qui montre que les vecteurs $\vec{EF}$ et $\vec{DG}$ ne sont pas orthogonaux, et donc que les droites (EF) et (DG) ne sont pas perpendiculaires.

EXERCICE 37 :

a) On a $\vec{BA} = -\vec{AB}$ et $\vec{BF} = \frac{1}{2}\vec{BA}$

donc $\vec{BA}.\vec{BF} = -\frac{1}{2}||\vec{BA}||^2 = -\frac{1}{2}AB^2$

b) On a $\vec{CF} = \frac{1}{2}\vec{CD}$

et donc $\vec{CF}.\vec{CD} = \frac{1}{2}||\vec{CD}||^2 = \frac{1}{2}CD^2 = \frac{1}{2}AB^2$

c) On a $\vec{AF} = \vec{AB}+\vec{BF}$

et donc $\vec{AF}.\vec{AB} = \vec{AB}^2 + \vec{AB}.\vec{BF} = AB^2 + \frac{1}{2}AB^2 = \frac{3}{2}AB^2$

d) On a $\vec{BE} = -\vec{BA}+\vec{BC} = -\vec{BA}$

et donc $\vec{AB}.\vec{BE} = -||\vec{AB}||^2 = -AB^2$

EXERCICE 38 :

a) $\vec{u}.\vec{v} = 2\times (-3)+1\times (-1) = -7$

b) $\vec{w}.\vec{v} = 1\times (-3)+4\times (-1) = -7$

c) $\vec{u}.(\vec{v}+\vec{w}) = \vec{u}.\vec{v}+\vec{u}.\vec{w} = -7-2 = -9$

d) $(-2\vec{u}).\vec{v}+3(\vec{v}.\vec{w}) = -4\times (-7)+3((-3)\times (1)+(-1)\times (4)) = 28-15 = 13$

EXERCICE 39 :

On a $\vec{u}.\vec{v} = (-3)\times (-8)+4\times (-6) = 24-24 = 0$

donc les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux.

EXERCICE 40 :

a) Un vecteur directeur de (d_1) est $\vec{u}_1 = (3;2)$ et un vecteur directeur de (d_2) est $\vec{u}_2 = (-2;3)$ .

On a $\vec{u}_1.\vec{u}_2 = 3\times (-2)+2\times 3 = 0$ donc les droites (d_1) et d2 sont perpendiculaires.

b) Un vecteur directeur de (d_1) est $\vec{u}_1 = (1;1)$ et un vecteur directeur de (d_2) est $\vec{u}_2 = (-1;1)$ .

On a $\vec{u}_1.\vec{u}_2 = 1\times (-1)+1\times 1 = 0$ donc les droites (d_1) et (d_2) sont perpendiculaires.

c) Un vecteur directeur de la droite (d_1) est $\vec{u}_1 = (-1;3)$ .

On a $\vec{u}_1.\vec{u}_2 = (-1)\times (-1)+3\times 3 = 1 \neq 0$ donc les droites (d_1) et (d_2) ne sont pas perpendiculaires.

EXERCICE 41 :

a) $\vec{u}.\vec{v} = (-2)\times (-1)+3\times (-5) = 1-15 = -14$

b) $(4\vec{u}).\vec{v} = 4(-2)\times (-1)+4\times 3\times (-5) = 8-60 = -52$

c) $(\vec{u}-\vec{v}).(\vec{u}+\vec{v}) = (\vec{u}.\vec{u}-\vec{v}.\vec{v}) = (||\vec{u}||^2-||\vec{v}||^2) = (4+9)-(1+25) = -13$

EXERCICE 42 :

On a $\vec{u}.\vec{v} = (-3)\times (-8)+4\times (-6) = 24-24 = 0$ donc les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux.

2. On a $\vec{AB} = (1-(-3);3-(-2)) = (4;5)$ et $\vec{u} = (-5;4)$ .

On a $\vec{AB}.\vec{u} = 4\times (-5)+5\times 4 = -20+20 = 0$ donc les vecteurs $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

EXERCICE 43 :

1. On utilise la loi des cosinus : $BC^2 = AB^2+AC^2-2\times AB\times AC\times \cos(\widehat{BAC}) = 9+16+12 = 37$ donc $BC = \sqrt{37}$

2. On utilise la loi des cosinus : $MP^2 = MN^2+NP^2-2\times MN\times NP\times \cos(\widehat{MNP}) = 25+49-70\times \cos(61^\circ) \approx 23,1$

donc $MP \approx \sqrt{23,1}$

3. On utilise la loi des cosinus :

$\cos(\widehat{EFG}) = \frac{EF^2+FG^2-EG^2}{2\times EF\times FG} = \frac{49+36-121}{2\times 7\times 6} = -\frac{1}{12} \\donc\\\\ \widehat{EFG} \approx 103 , 6^\circ$

4. On utilise la loi des cosinus :

$\cos(\widehat{EDF}) = \frac{EF^2+DF^2-ED^2}{2\times EF\times DF} = \frac{25+64-81}{2\times 5\times 8} = \frac{1}{8}\\\\ donc \\\\\widehat{EDF} \approx 82{,}5^\circ$

EXERCICE 44 :

a) On a $\vec{u}.(\vec{u}+\vec{v}) = \vec{u}.\vec{u}+\vec{u}.\vec{v} = a^2$

b) On a $(2\vec{u}-3\vec{v}).\vec{v} = 2\vec{u}.\vec{v}-3\vec{v}.\vec{v} = -3b^2$

c) On a $(\vec{u}+\vec{v})^2 = \vec{u}^2+2\vec{u}.\vec{v}+\vec{v}^2 = a^2+b^2$

EXERCICE 45 :

On a $\vec{v} = 3\vec{u}$ donc $\vec{u}.\vec{v} = 3a^2$ .

Les vecteurs $\vec{u}$ et $\vec{w}$ sont orthogonaux donc $\vec{u}.\vec{w} = 0$ .

On a $\vec{u}+\vec{w} = (\vec{u}+\vec{v})+(\vec{w}-\vec{v}) = \frac{a}{\sqrt{10}}\times (3\vec{u}+\vec{w})-\frac{3a}{\sqrt{10}}\times \vec{v}$

donc $(\vec{u}+\vec{v}).(\vec{u}+\vec{w}) = \frac{a^2}{10}(3a^2)+0 = \frac{3}{10}a^4$ .

On a $(\vec{u}+\vec{w})^2 = \vec{u}^2+2\vec{u}.\vec{w}+\vec{w}^2 = a^2+121a^2 = 122a^2$ .

EXERCICE 46 :

a) On a

$\vec{AB}.\vec{CD} = |\vec{AB}|\times |\vec{CD}|\times \cos(\widehat{AB,CD}) = AB\times DC\cos(\widehat{DC,AB}) = BA\times DC$

b) On a

$\vec{AB}.\vec{CD}+\vec{AB}.\vec{CE} = \vec{AB}.(\vec{CD}+\vec{CE}) = \vec{AB}.\vec{DE} = \vec{AB}.\vec{ED} = \vec{AB}.\vec{EC}+\vec{AB}.\vec{CD}$

c) On a

$\vec{AB}.\vec{AC} = AB\times AC\cos(\widehat{AB,AC}) = AB\times AC\cos(\widehat{BAC}-\widehat{CAB}) = AB(AB-BC) = AB^2-BA\times BC$

EXERCICE 47 :

1. Soit M un point du plan. On a $\vec{MA}+\vec{MB} = \vec{AB}$

donc

$(\vec{MA}+\vec{MB})^2 = \vec{AB}^2 = 144$

ce qui donne

$\vec{MA}^2+2\vec{MA}.\vec{MB}+\vec{MB}^2 = 144$ .

Comme I est le milieu de [AB], on a $\vec{MA}=\vec{MI}-\vec{AI}$ et $\vec{MB} = \vec{MB}-\vec{AI}$ .

En injectant ces expressions dans l’équation précédente, on obtient

$\vec{MI}.\vec{AI}+\vec{MI}.\vec{BI}+\vec{BI}.\vec{AI} = 68$ .

Posons $\vec{MI} = (x;y)$ et $\vec{AI} = (-\frac{1}{2};0)$ .

On a alors $\vec{BI} = (x+\frac{1}{2};y)$ et donc $\vec{MI}.\vec{AI} = -\frac{x}{2}$ .

En injectant ces expressions dans l’équation précédente et en développant, on obtient l’équation suivante :

$-\frac{x}{2}+2(x+\frac{1}{2})y+4y^2 = 68$ .

Ce qui donne l’équation suivante pour y : $4y^2+4xy-31 = 0$ .

Cette équation admet des solutions réelles si et seulement si le discriminant est positif, ce qui donne $x^2\geq\, 31$ .

Ainsi, l’ensemble des points M qui vérifient l’équation est l’ensemble des points situés à l’extérieur ou sur le cercle de centre I et de rayon $\sqrt{31}$ .

2. Soit M un point du plan.

On a $\vec{MC}+\vec{MD} = \vec{CD} = \sqrt{100} = 10$

donc

$(\vec{MC}+\vec{MD})^2 = \vec{CD}^2 = 100$ ce qui donne $\vec{MC}^2+2\vec{MC}.\vec{MD}+\vec{MD}^2 = 100$ .

Comme H est le milieu de [CD], on a $\vec{MC}=\vec{MH}-\vec{CH}$ et $\vec{MD} = \vec{MD}-\vec{DH}$ .

En injectant ces expressions dans l’équation précédente, on obtient $\vec{MH}.\vec{CH}+\vec{MH}.\vec{DH}+\vec{CH}.\vec{DH} = -49$ .

Posons $\vec{MH} = (x;y)$ et $\vec{CH} = (5;0)$ .

On a alors $\vec{DH} = (x-5;y-10)$ et donc $\vec{MH}.\vec{CH} = 5x$ .

En injectant ces expressions dans l’équation précédente et en développant, on obtient l’équation suivante : $10y-95 = 0$ .

Ainsi, l’ensemble des points M qui vérifient l’équation est la droite passant par H et parallèle à la droite (CD).

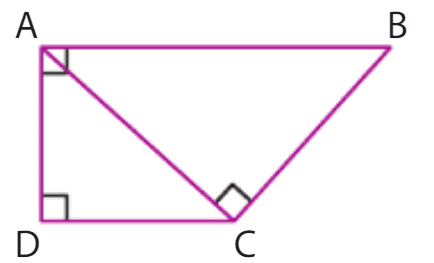
EXERCICE 48 :

On a $\vec{AB} = (1;a)$ et $\vec{AC} = (-a;1)$ .

On a $\vec{AB}.\vec{AC} = -a+a = 0$ .

D’un autre côté, on a $AB^2+BC^2 = a^2+(a-1)^2 = 2a^2-2a+1 = (a-1)^2 + a^2+1 = AC^2+BD^2$ donc les triangles ABD et BCD sont rectangles en B et C respectivement et $AC^2 = AB^2+BC^2 = AB\times CD$ .

EXERCICE 49 :

A. Avec coordonnées
1. Les coordonnées des points sont : $A(0,0), B(1,0), C(-a+1,a), D(-a, a), E(0,a), F(a,a), G(a+1,0)$ ,

donc il suffit de trouver les coordonnées du point G.

Le vecteur $\vec{GB}$ est égal à $\vec{GE}+\vec{EA}+\vec{AB} = (-a+1,a)+(0,a)+(1,0) = (2-a,2a)$

donc les coordonnées de G sont (2-a,a) .
2. Les droites (AG) et (CE) sont perpendiculaires si et seulement si $\vec{AG}.\vec{CE} = 0$ .

On a $\vec{AG} = (-a+1,a)$ et $\vec{CE} = (-a,a-1)$

donc $\vec{AG}.\vec{CE} = -a(a-1)+(a)(a-1) = 0$ .

B. Sans coordonnées
1. On a

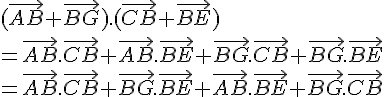
$(\vec{AB}+\vec{BG}).(\vec{CB}+\vec{BE}) \\\\= \vec{AB}.\vec{CB}+\vec{AB}.\vec{BE}+\vec{BG}.\vec{CB}+\vec{BG}.\vec{BE} \\\\= \vec{AB}.\vec{CB}+\vec{BG}.\vec{BE}+\vec{AB}.\vec{BE}+\vec{BG}.\vec{CB}$ .

Comme les vecteurs $\vec{AB}$ et $\vec{CB}$ sont orthogonaux et de même norme, on a $\vec{AB}.\vec{CB} = \vec{CB}^2-\vec{BQ}^2 = (a-1)^2+a^2 = 2a^2-2a+2$ .

De même, on a $\vec{BG}.\vec{BE} = \vec{BE}^2-\vec{BQ}^2 = (a^2+1)-a^2 = 1$ .

Il reste donc à calculer les produits scalaires $\vec{AB}.\vec{BE}$ et $\vec{BG}.\vec{CB}$ .

On a $\vec{AB}.\vec{BE} = \vec{AB}.\vec{BC}-\vec{EC}.\vec{AB} = -a+1$

et $\vec{BG}.\vec{CB} = \vec{BG}.\vec{BC}-\vec{CG}.\vec{BG} = a+1$ .

En injectant ces calculs dans l’expression précédente, on obtient $2a^2-2a+2+1+a^2-1-a^2-a = 0$ ce qui donne a = 0.

Ainsi, les droites (AG) et (CE) sont perpendiculaires.

EXERCICE 50 :

A. Sans coordonnées
1. On a $AD+AE = a\sqrt{2}+a = 2a\frac{\sqrt{2}}{2}+2a\frac{\sqrt{2}}{2}+\sqrt{2}a = 2Al$ .
2. On a

$(AD+AE).(AB+AG) = AD.AB+AD.AG+AE.AB+AE.AG = a^2+(a+a)\times (-a)+(a+a)\times (a)+(a+a)\times (0) = 0$ .

Donc les droites (AI) et (BG) sont perpendiculaires.

B. Avec coordonnées
1. On a A(0,0), $I(-\frac{a}{2},\frac{a}{2}), B(a,0)$ et $G(2a,\frac{a}{2})$ .
2. Les vecteurs $\vec{AI} = (-\frac{a}{2},\frac{a}{2})$ et $\vec{BG} = (a,\frac{a}{2})$ sont-ils orthogonaux ?

On a $\vec{AI}.\vec{BG} = -\frac{a^2}{2}+a\frac{a}{2} = \frac{a^2}{2} \neq 0$ , donc les droites ne sont pas orthogonales.

Avec les coordonnées, on peut également calculer les équations des droites (AI) et (BG) et vérifier qu’elles sont perpendiculaires (on peut utiliser la méthode des coefficients directeurs).

EXERCICE 51 :

1.
a) On utilise le repère (A;B,D) et on note (x;y) les coordonnées de M.

Les coordonnées de H sont (x,0) et les coordonnées de K sont (0,y).

Les coordonnées de C sont $(\frac{y}{2},\frac{y}{2})$ car AC est la diagonale du carré.

Les coordonnées de D sont $(\frac{1-x}{2},\frac{1-x}{2})$ .

Les vecteurs CK et DH sont alors respectivement $(\frac{y}{2},\frac{y}{2})-(0,y) = (\frac{y}{2},-\frac{y}{2})$ et $(\frac{x}{2},-\frac{x}{2})-(x,0) = (-\frac{x}{2},-\frac{x}{2})$ et leur produit scalaire vaut $-\frac{xy}{2}+\frac{xy}{2}=0$ , donc les droites (CK) et (DH) sont perpendiculaires.
b) On a $\vec{BK} = (0,y)$ et $\vec{DH} = (x,0)-(x,y)\times \frac{(0,1).(x,y)}{\|(x,y)\|^2} = (x,\frac{x^2-y^2}{x^2+y^2})$

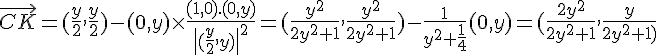
et $\vec{CK} = (\frac{y}{2},\frac{y}{2})-(0,y)\times \frac{(1,0).(0,y)}{\|(\frac{y}{2},y)\|^2} = (\frac{y^2}{2y^2+1},\frac{y^2}{2y^2+1})-\frac{1}{y^2+\frac{1}{4}}(0,y) = (\frac{2y^2}{2y^2+1},\frac{y}{2y^2+1)}$ .

On a donc $\vec{CK}.\vec{DH} = \frac{2xy^2}{(2y^2+1)^2}-\frac{xy^2}{(x^2+y^2)(2y^2+1)}-\frac{xy^2}{(x^2+y^2)(2y^2+1)}+\frac{y^3}{(x^2+y^2)(2y^2+1)} = \frac{-xy(x^2-y^2)}{(x^2+y^2)(2y^2+1)} = 0$

donc les droites (CK) et (DH) sont perpendiculaires.

2.
a) On utilise le repère (A;B,D) et on note (x;y) les coordonnées de M. Les coordonnées de H sont (x,0) et les coordonnées de K sont (0,y) .

Pour démontrer que les longueurs DH et CK sont égales, on calcule les coordonnées de leur milieu et on montre qu’elles sont égales. Les coordonnées du milieu de DH sont $(\frac{x}{2},-\frac{x}{2})$ et les coordonnées du milieu de CK sont $(\frac{y^2}{2y^2+1},\frac{y}{2y^2+1})$ .

On a donc à montrer que $\frac{x}{2}=\frac{y^2}{2y^2+1}$ et $-\frac{x}{2}=\frac{y}{2y^2+1}$ , ce qui est vérifié en remplaçant y par $\frac{\sqrt{2}}{2}$ et en utilisant le fait que $x = 1-\frac{\sqrt{2}}{2}y$ .
b) On peut également utiliser la géométrie pour démontrer que DH et CK ont même longueur. On remarque que les triangles DMH et DCK sont semblables, donc $\frac{DH}{CK}=\frac{HM}{CK}=\frac{CK}{CM}=\frac{CK}{CD}=\frac{1}{\sqrt{2}}$ . De plus, les triangles DHC et CKM sont semblables, donc $\frac{CD}{CK}=\frac{DH}{CM}=\sqrt{2}$ , donc DH=CK.

4.4/5 - (20878 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «produit scalaire : corrigé des exercices de maths en 1ère en PDF.» au format PDF.

Ressources de première

Cours de première

Les suites numériques

Angles orientés et repérage polaire

Le produit scalaire dans le plan

Equations et inéquations du second degré

Généralités sur les fonctions numériques

Probabilités

Exercices de première

Produit scalaire

Géométrie dans l’espace

Les suites

Les équations et inéquations du second degré

Dérivée d’une fonction

Angles orientés et repérage polaire

D'autres cours et exercices à consulter

Fonction exponentielle : corrigé des exercices de maths en terminale en PDF.

Géométrie dans l’espace : corrigé des exercices en 1ère en PDF.

Angles orientés, repérage et polaire : corrigé des exercices en 1ère en PDF.

Fonctions : corrigé des exercices de maths en 1ère en PDF.

Limites de fonctions : corrigé des exercices de maths en 1ère en PDF.

Statistiques : corrigé des exercices de maths en 1ère en PDF.

Barycentre : corrigé des exercices de maths en 1ère en PDF.

Suites : corrigé des exercices de maths en 1ère en PDF.

Exercices de maths interactifs avec saisie au clavier des réponses.

Maths et programmation dans un escape game.

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Produit scalaire : corrigé des exercices de maths en 1ère en PDF.

Ressources de première

Cours de première

Exercices de première

D'autres cours et exercices à consulter

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques