Dans cette leçon en première, nous étudierons deux familles de suites particulières, les suites arithmétiques et géométriques ainsi que leur sens de variation suivant la valeur de la raison puis, nous terminerons avec le calcul de la somme des n premiers termes d’une suite numérique.
I. Définition
Une suite numérique 
est une fonction de dans : .
Son ensemble de définition est donc ou un sous-ensemble de .
II. Notations – Vocabulaire
La variable n étant un nombre entier naturel, cet entier n permet de numéroter les images : en plus de l’écriture fonctionnelle classique s(n) utilisée pour désigner l’image de l’entier naturel n par la fonction s, on peut aussi utiliser la notation indexée (ou indicée): sn . Avec cette notation l’image de 0 s’écrit : s0.
· Avec cette notation, on dit que :
- s(n) = sn est le terme d’indice n ou de rang n de la suite s.
- s est la suite de terme général sn et l’on écrit : s = (sn)
- s(0) = s0 qui est l’image de 0 par s est aussi appelé terme de rang 0 de la suite s .
- s(1) = s1 qui est l’image de 1 par s est aussi appelé terme de rang 1 de la suite s.
Si la numérotation commence au rang 0, s(0) = s0 est le premier terme de la suite s . s(1) = s1 est le second terme de la suite s.
Il arrive parfois que le premier terme d’une suite s ne soit pas s0 .
Exemple :
n’existe pas pour n = 0. La suite commence au rang 1. On écrira alors: pour .
n’existe pas pour n = 0, ni pour n = 1. La suite commence au rang 2.
Dans tous les cas de ce type-là, on précisera le sous-ensemble de où la suite est définie: Ici, on a : .
III. Diverses manières de définir une suite
1. Suites définies par une formule de fonction:
Pour cela, la plupart du temps, on restreint à une fonction définie sur ou un sous-ensemble de contenant .
Par exemple, la suite un = n2 ( ), est la restriction à n de la fonction f définie sur par f(x) = x2 .
Ainsi, les propriétés déjà étudiées pour les fonctions de la variable réelle seront utilisables pour les suites!
Nous étudierons cependant aussi quelques exemples de suites associées à des fonctions que vous n’avez pas encore étudiées en 1ère ; par exemple, la suite géométrique un = 2n est associée à la fonction exponentielle définie sur par f(x) = 2x qui sera étudiée en classe terminale.
2. Suites définies par une formule de récurrence:
Pour tout entier naturel n, l’image s(n) = sn est « numérotable ».
On peut définir le terme de rang (n+1) en fonction du terme précédent de rang n par une formule appelée formule de récurrence.
Plus précisément, la suite s = (sn) sera définie par récurrence par:
- Son premier terme .
- · Une égalité reliant deux termes consécutifs quelconques de la suite:
- où est une fonction connue.
Exemple :
La suite définie par son premier terme u0 = 4096 et la formule de récurrence vérifiée pour tout entier n: .
On obtient : u1 = = = 64
u2 = = = 8
u3 = =
u4 = =
u5 = …. et ainsi de suite …
Ici la fonction f est définie par .
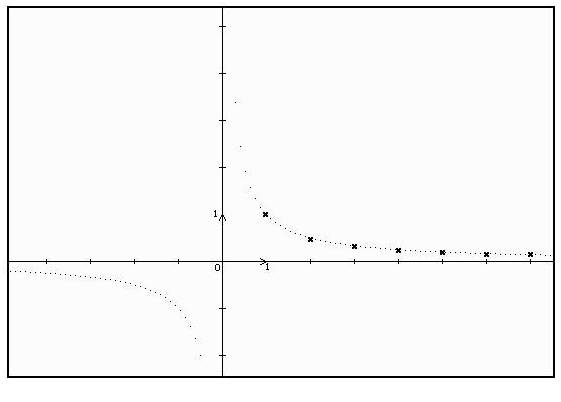
IV. Représentations graphiques de suites
, la représentation traditionnelle des graphiques de fonction est utilisable: On obtient alors les points d’abscisses entières du graphique de la fonction de la variable réelle x: .Exemple :
Le graphique de la suite définie sur par: , correspond aux point d’abscisses de la fonction définie sur par .
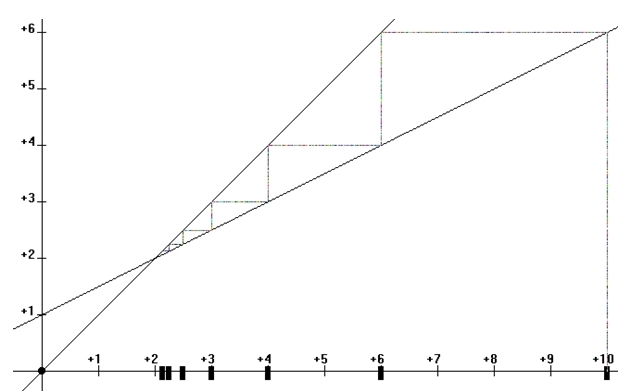
Lorsque la suite est définie par une formule de récurrence du type , cette représentation n’est plus directement réalisable.
On a alors recours à une représentation de type « toile d’araignée » .
Exemple :
Sur le graphique ci-dessus, sont tracées les droites d’équation et y = x.
Ce dispositif permet de visualiser les termes successifs de la suite définie sur par :
u0 = 10 et , pour tout :
En effet :
V. Suites monotones.
1. Sens de variation d’une suite.
|
Si pour tout |
|
|
|
|
Sens de variation de |
|
|
|
|
Variation absolue |
|
|
|
|
Quotient (termes strictement positifs) |
|
|
|
VI. Suites bornées, majorées, minorées.
Mêmes définitions que pour les fonctions de la variable réelle.
Exemple :
La suite sn = sin n est une suite bornée. En effet: elle est majorée par 1 et minorée par (-1).
VII. Suites périodiques.
On dit qu’une suite est périodique de période , lorsque, pour tout , on a: , p étant le plus petit entier naturel non nul vérifiant ceci.
Exemple :
Les suites constantes sont périodiques de période 1.
La suite est périodique de période 2.
VIII. Suites arithmétiques.
Lorsque l’on passe de n’importe quel terme d’une suite au terme suivant, en additionnant (ou en soustrayant) toujours le même nombre, on dit que la suite est arithmétique.
C’est à dire que, s’il existe , tel que, pour tout , on ait :
, on dit alors que la suite est arithmétique de raison r.
Les accroissements d’une suite arithmétique sont donc constants : cette constante est la raison r de la suite arithmétique.
Exemples :
- La suite des entiers naturels est arithmétique de premier terme 0 et de raison 1.
- La suite des entiers naturels pairs est arithmétique de premier terme 0 et de raison 2.
- La suite des entiers naturels impairs est arithmétique de premier terme 1 et de raison 2.
- La suite constante de terme général Un = 2 est arithmétique de premier terme 2 et de raison 0.
IX. Suites géométriques.
Lorsque l’on passe de n’importe quel terme d’une suite au terme suivant, en multipliant (ou en divisant) toujours par le même nombre non nul, on dit que la suite est géométrique.
C’est à dire que, s’il existe , tel que, pour tout , on ait :
, on dit alors que la suite est géométrique de raison .
Les coefficients multiplicateurs d’une suite géométrique sont donc constants : cette constante est la raison q de la suite géométrique.
Les taux d’accroissements d’une suite géométrique sont aussi constants. En effet :
.
La suite géométrique de raison q possède donc un taux d’accroissement constant t = q – 1.
Exemple :
La suite constante de terme général Un = 2 est géométrique de premier terme 2 et de raison 1.
La suite de terme général Un = (-1)n est géométrique de premier terme U0 = 1 et de raison -1.
Remarque :
- Une suite dont les variations absolues successives Sn+1 – Sn = r sont constantes, c’est à dire indépendantes de n, est une suite arithmétique de raison r.
- Une suite dont les variations relatives successives sont constantes , c’est à dire indépendantes de n, est une suite géométrique de raison q = 1 + t.
Par exemple, avec une augmentation relative de t = 5 % = 0,05 , alors, q = 1,05 .
En effet, si 0,05 , alors : Sn+1 – Sn = 0,05 Sn .
Donc : Sn+1 = Sn + 0,05 Sn = (1 + 0,05) Sn .
Cela donne : Sn+1 = 1,05 Sn .
On a donc une suite géométrique de raison q = 1,05.
Et dans le cas général, si , alors : .
Donc : .
On a donc une suite géométrique de raison .
X. Suites arithmétiques et géométriques : résumé.
S est une suite et n un entier naturel quelconque :
|
Suite arithmétique de raison r |
Suite géométrique de raison q ¹ 0 |
|
| formule de récurrence |
|
|
| caractérisations |
|
si |
| terme de rang n : formule de fonction |
1er terme + n fois la raison
|
1er terme
|
XI. Quelques remarques intéressantes.
1. Suites arithmétiques.
La suite définie par la formule: (fonction affine de ) est la suite arithmétique de premier terme et de raison .La représentation graphique d’une suite arithmétique est donc formée de points alignés.
2. Suites géométriques.
La suite des puissances d’un nombre réel a non nul, de terme général est
la suite géométrique de premier terme et de raison .
La représentation graphique d’une suite géométrique de raison différente de 1 est donc formée de points qui ne sont pas alignés (ils sont situés sur une courbe exponentielle).
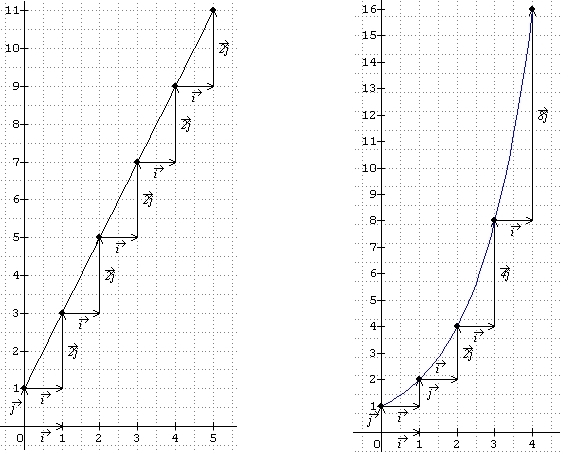
3. Illustrations graphiques.
4. Suites arithmétiques et sens de variation.
(un) est une suite arithmétique de raison r.
- Si r > 0, alors (un) est strictement croissante.
- Si r < 0, alors (un) est strictement décroissante.
- Si r = 0, alors (un) est constante.
5. Suites géométriques et sens de variation.
(un) est une suite géométrique raison et de premier terme .
- Si q < 0, alors (un) n’est pas monotone (les termes sont alternativement positifs, puis négatifs).
- Si q > 1 et si u0 > 0 , alors (un) est strictement croissante.
- Si q > 1 et si u0 < 0 , alors (un) est strictement décroissante.
- Si 0 < q < 1 et si u0 > 0 , alors (un) est strictement décroissante.
- Si 0 < q < 1 et si u0 < 0 , alors (un) est strictement croissante.
- Si q = 1, alors (un) est constante.
6.Suites arithmétiques et somme de termes consécutifs.
Si est une suite arithmétique de raison r, alors, pour tout , on a :
égalité qui s’écrit aussi : .
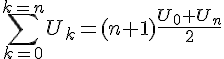
Pour utiliser cette formule, il peut être utile de voir que : .
En particulier :
7. Suites géométriques et somme de termes consécutifs.
Si est une suite géométrique de raison , alors, pour tout , on a :
égalité qui s’écrit aussi :
.
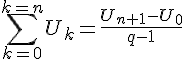
Pour utiliser cette formule, il peut être utile de voir que :
.
En particulier : .
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les suites numériques : cours de maths en 1ère en PDF.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
