Fonction exponentielle : exercices de maths en 1ère corrigés en PDF.

Mis à jour le 29 mai 2025

Sommaire

✏️Exercices

1ère • Lycée

Fonction exponentielle

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les fonctions exponentielles à travers des exercices de maths en 1ère corrigés.Vous pouvez également consulter les énoncés avec des difficultés croissantes et les réponses correspondantes afin de repérer vos erreurs.

Exercice 1 – Primitive d’une fonction composée
Soit la fonction f définie par $f(x) = (x - 3)^{\frac{2}{3}}$
1. Donner le domaine de définition de la fonction f.
2. Donner une primitive de la fonction.

Exercice 2 – Fonctions puissances
soit la fonction f tel que :
1. Indiquer le domaine de définition de f et transformer l’écriture du réel f(x).
2. Donner un prolongement par continuité de f au point 0.
3. Etudier la dérivabilité de f au point 0.
4. Calculer la dérivée de f et étudier son signe. Etablir le tableau de variations.
5. Décrire comment se présente la tangente en ce point.
6. Construire la courbe dans un repère approprié.

Exercice 3 – Restitution organisée de connaissances
On supposera connus les résultats suivants :
* e^0=1
* Pour tous réels x et y, $e^x\times e^y=e^{x+y}$ .
1. Démontrer que pour tout réel x, $e^{-x}=\frac{1}{e^x}$ .
2. Démontrer que pour tout réel x et pour tout entier naturel n,
$(e^{x})^n=e^{nx}$

Exercice 4 – Résoudre les inéquations suivantes :
1. $x^{\pi}<\frac{1}{2}.$
2. $3^x\geq\, 4.$

Exercice 5 – Primitives de fonctions exponentielles
Déterminer les primitives des fonctions suivantes :
1. $f(x)=sinx\times e^{cosx}$ .
2. $f(x)=x^{-2}e^{\frac{1}{x}}\,sur\,]-\infty;0[.$

Exercice 6 – Etude d’une fonction

Soit pour x ∈ R.

1. Déterminez les limites de f aux bornes du domaine de déﬁnition.

2. Etudier les variations de f.

3. Construisez la courbe C représentant f.

Exercice 7 – Résoudre les équations et inéquations proposées
$1.e^{2x^2+3}=e^{7x}.\\2.\,2e^{-x}=\frac{1}{e^x+2}.\\3.\,e^x\leq\, \frac{1}{e^x}.$

Exercice 8 – Bénéfice d’une entreprise
Une entreprise fabrique et vend chaque jour un nombre x d’objets. Chaque objet est vendu 100 .
Le coût de production unitaire C_u(x) exprimant le coût de production par objet produit est :
$C_u(x)=x-10+\frac{900}{x}$ pour x dans [10 ; 100]
1.a) Montrer que $C^'_u(x)=\frac{(x-30)(x+30)}{x^2}$ .
b) Etudier le signe de sur [10 ; 100] et en déduire le tableau de variation de la fonction C_u sur [10 ; 100].
c) Déterminer pour quelle production le coût unitaire est le plus bas. Déterminer alors le bénéfice de l’entreprise.
2. Montrer que le bénéfice global de l’entreprise s’exprime par : B(x ) = −x² +110x − 900.
3. Déterminer son sens de variation sur [10 ; 100] et déterminer la production qui donne un bénéfice maximal. Quel est ce
bénéfice ?

Exercice 9 – Problème de courbe
La courbe représente une fonction f définie par f(x)= (ax+b)exp(-x).
Elle passe par les points de coordonnées (o;2) et (-2;0).
1) Calculer a et b .
2) Déterminer les coordonnées du maximum après avoir étudié les variations de f.

Exercice 10 – Logarithme et exponentielle
Simplifier au maximum :
$A=ln(\sqrt{80})-\frac{1}{2}ln5$
$B=ln(\sqrt{6}-1)+ln(\sqrt{6}+1)-ln(\sqrt{100})-ln\frac{1}{8}$

Exercice 11 – Calcul de dérivées et de limites
Calculez les dérivées et les limites aux bornes des ensembles de déﬁnitions des

fonctions déﬁnies par les expressions suivantes :

$1.f(x)=e^{4x+1}\\2.f(x)=e^x+x^2+1\\3.f(x)=5e^x+5xe^x\\4.f(x)=\frac{e^x+1}{e^x-1}\\5.f(x)=\frac{3x+1-e^x}{e^x}\\6.f(x)=x^3e^{-x}$

Exercice 12 – Simplifier des exponentielles

Simplifier au maximum les expressions suivantes :

$1. e^xe^{-x.}\\2.e^xe^{-x+1}\\3.ee^{-x}\\4.(e^{-x})^2\\5.\frac{e^{2x}}{e^{2-x}}\\6.\frac{(e^x)^3}{e^{2x}}$

Exercice 13 – Résoudre des équations et inéquations contenant des exponentielles
Résoudre les équations et inéquations :

$e^{2x}+3e^x-4=0$
$e^{3x}-e^x=0$
$e^x+e^{-x}=1$
$e^{2x-1}<\sqrt{e}$
$4e^{2x}<3e^x+1$
$e^{\frac{^2x-1}{3x+1}}>\frac{1}{e^2}$

Exercice 14 – Etude de l’équation lnx=x^n

Exercice 15 -Courbe de Gauss
soit $k\in\mathbb{R}^{+*}$ .On définit sur $\mathbb{R}$ , la fonction G_k par $G_k(x)=e^{-kx^2}$ .
1.Etudier la parité de G_k .
2.Démontrer G_k que est dérivable et calculer sa dérivée.En déduire le tableau de variations de G_k .
3.Calculer G'_k et résoudre .
4.Tracer les courbes de G_k pour $k=\frac{1}{2};1;2$ .
5.Démontrer que $h\leq\,,k\Leftrightarrow,G_h\geq\,,G_k$ sur $\mathbb{R}$ .
6.Dans cette question $k=\frac{1}{2}$ .Soit $\alpha$ la solution positive de l’équation .
7.Déterminer une équation de la tangente T à la courbe de G_k au point d’abscisse $\alpha$ .
8.Tracer T sur le graphique.

Exercice 16 -Extrait baccalauréat.

Partie A
On donne un entier naturel n strictement positif, et on considère l’équation différentielle :
$(E_n)\,\,y'+y=\frac{x^n}{n!}e^{-x}$
1. On fait l’hypothèse que deux fonctions g et h, définies et dérivables sur $\mathbb{R}$ , vérifient, pour tout x réel :
$g(x)=h(x)e^{-x}$
a. Montrer que g est solution de (E_n) si et seulement si, pour tout x réel :
$\,\,h'(x)=\frac{x^n}{n!}$ .
b. En déduire la fonction h associée à une solution g de (E_n) , sachant que f(0)=0.
Quelle est alors la fonction g?
2. Soit $\phi$ une fonction dérivable sur $\mathbb{R}$ .
a. Montrer que $\phi$ est solution de (E_n) si et seulement si $\phi - g$ est solution de l’équation :
(F) y’+y=0
b. Résoudre (F) .
c. déterminer la solution générale $\phi$ de l’équation (E_n) .
d. Déterminer la solution f de l’équation (E_n) vérifiant f(0)=0 .

Partie B
Le but de cette partie est de montrer que :
$\fbox{\lim_{n \to +\infty}(\sum_{k=0}^{n}\frac{1}{k!})=e}$
1. On pose, pour tout x réel,
$f_0(x)=e^{-x}\,,\,f_1(x)=xe^{-x}$ .
a. vérifier que f_1 est solution de l’équation différentielle : y’+y= f_0 .
b. Pour tout entier strictement positif n, on définit la fonction f_n comme la solution de l’équation différentielle y’+y= $f_{n-1}$ vérifiant .
En utilisant la partie A, montrer par récurrence que , pour tout x réel et tout entier $n\ge 1$ :
$f_n(x)=\frac{x^n}{n!}e^{-x}$ .
2. Pour tout entier naturel n, on pose :
$I_n=\int_{0}^{1} f_n(x)dx$
a. Montrer, pour tout entier naturel n et pour tout x élément de l’intervalle [0;1], l’encadrement :
$0\le f_n(x)\le \frac{x^n}{n!}$ .
En déduire que $0\le I_n\le \frac{1}{(n+1)!}$ , puis déterminer la limite de la suite ( I_n) .
b. Montrer, pour tout entier naturel k non nul, l’égalité :
$\fbox{I_k-I_{k-1}=-\frac{1}{k!}e^{-1}}$ .
c. Calculer I_0 et déduire de ce qui précède que :
$I_n=1-\sum_{k=0}^{n}\frac{e^{-1}}{k!}$ .
d. En déduire finalement :
$\fbox{\lim_{n \to +\infty}(\sum_{k=0}^{n}\frac{1}{k!})=e}$

Exercice 17 :

Ecrire à l’aide d’une seule exponentielle :

a. $\frac{1}{e^3}$

b. $e^{-2}\times \,e^7$

Exercice 18 :

f est une fonction dérivable sur $\mathbb{R}$ telle que $f'=f\,\,et\,\,f(0)=-\frac{1}{2}$ .

g est la fonction définie sur $\mathbb{R}$ par .

Vérifier que g est dérivable sur $\mathbb{R}$ et que g’ = g.
Calculer g(0); en déduire l’expression de g(x).
En déduire l’expression de f(x).

Exercice 19 :

Dans chaque cas, écrire l’expression avec une seule exponentielle.

a. $e^4\times \,e^6$

b. $e\times \,(e^5)^2$

c. $\frac{e^{30}\times \,e^{-10}}{e^{10}}$

2. a désigne un nombre réel, simplifier l’écriture de chaque expression :

$a)\,\,\frac{e^{2a}\times \,e^{-a}}{e^{5a}}\,\,;b)\,\,\frac{e^{2a}+1}{e^{1-a}}\,\,;\,\,c)(e^a)^3\times \,e$

Exercice 20 :

f est la fonction définie sur $]-1;+\infty[$ par $f(x)=\frac{e^x}{1+x}$ .

Dans un repère, $\xi$ est la courbe représentative de la fonction f et T_a est la tangente à $\xi$ au point A d’abscisse a avec a>-1 .

1. donner une équation de T_a .

2. Démontrer qu’il existe deux valeurs de a pour lesquelles T_a passe par l’origine du repère.

Exercice 21 :

On modélise la température moyenne T à l’intérieur d’un congélateur en posant :

$T(t)=19,5e^{-7\times \,10^{-4}t}-10,5$ où $t\in[0;+\infty[$ correspond au temps, exprimé en minutes, écoulé

depuis sa mise en marche et T(t) sa température en °C.

1. Donner la température moyenne à l’intérieur du congélateur :

a. avant sa mise en marche;

b. après une journée de fonctionnement.

2. Etudier la limite de T en $+\infty$ et interpréter le résultat obtenu.

Exercice 22 :

Ecrire les réels donnés sous la forme exponentielle e^k où k est un entier.

$1)e^{-7}\times \,e^3$

$2)e^{-1}\times \,e^{-5}$

$3)e^2,\times \,e$

$4)e\times \,e^{-1}$

$5)\frac{1}{e}$

$6)\frac{1}{e^{-1}}$

$7)\frac{1}{e^2}$

$8)\frac{1}{e^{-3}}$

$9)\frac{e^{-3}}{e^2}$

$10)\frac{e}{e^{-1}}$

$11)\frac{e^{-2}}{e}$

$12)\frac{e^2\times \,e^{-3}}{e^5}$

$15)(e^{-1})^6$

$16)e\times \,(e^{-1})^3$

Exercice 23 :

Ecrire l’expression donnée sous la forme e^A où A est une expression.

$1)e^x,\times \,e^2$

$2)e^{-1}\times \,e^{-x}$

$3)e\times \,e^x$

$4)e^x\times \,e^x$

$5)e^x\times \,e^{-x}$

$6)e^{x-1}\times \,e^x$

$8)(e^{-x+1})^3$

$10)\frac{e^{5x}}{e^x}$

$11)\frac{e^{x+1}}{e}$

$12)\frac{e^3}{e^{2x-1}}$

Exercice 24 :

On donne l’expression de trois fonctions f,g et h définies et dérivables sur $\mathbb{R}$ .

Calculer la dérivée des fonctions f, g et h.

$1)f(x)=e^{0,5x};g(x)=e^{3x};h(x)=e^{-x}$ .

$2)f(x)=e^{x+1};g(x)=e^{1-2x};h(x)=e^{-3x+1}$

$3)f(x)=2+e^{2x};g(x)=1-e^{-2x};h(x)=e^{-3x+1}$

$4)f(x)=2+e^{2x};g(x)=1-e^{-2x};h(x)=1+2e^{-x}$

Exercice 25 :

On estime que les futures découvertes de pétrole dans le monde peuvent être modélisées,
à partir de 2015, par la fonction f définie sur [15 ; + $\infty$ [ par:

$f(x)=17280e^{-0,024x}$

où f(x) représente, en millions de barils, l’estimation de la quantité
de pétrole qui sera découverte au cours de l’année 2000 + x.
1. Déterminer la limite de la fonction f en + $\infty$ .

2. Calculer f ‘ (x) et en déduire le sens de variation de la fonction f sur l’intervalle [15 ; + $\infty$ [.
3. Interpréter les résultats des questions 1 et 2.

Exercice 26 :

Soit f la fonction définie sur $\mathbb{R}$ par .

Exprimer $f\,'\,(x)$ en fonction de x.

2) Justifier que, pour tout réel x de l’intervalle $[0;+\infty[$ , $f'(x)\leq\,\,0$ .

3) En déduire les variations de la fonction f sur $\mathbb{R}$ .

Exercice 27 :

Ecrire les expressions suivantes sous la forme exponentielle e^A , où A est une expression.

$1)\frac{e^{2x+1}}{e^{1-x}}$

$2)\frac{e^{-x+2}\times \,e^{-2x-1}}{e^{3x+2}\times \,e^{-x-1}}$

$3)\frac{(e^{-x})^2\times \,e^{-x+1}}{e^{x+2}\times \,(e^{-x-1})^3}$

Exercice 28 :

Démontrer les égalités suivantes :

Pour tout réel x, $-2e^{2x}+3e^x+2=(1-2e^x)(2-e^x)$ .

Pour tout réel x, $\frac{e\times \,e^x}{e^{2+3x}}=(e^{-x-0,5})^2$ .

Pour tout réel x, $\frac{e^{1-3x}}{1+e^{-3x}}=\frac{e}{e^{3x}+1}$

Exercice 29 :

1)Démontrer que l’équation $e^x-2e^{-x}+1=0$ est équivalente à l’équation .

2)Résoudre dans $\mathbb{R}$ l’équation $e^x-2e^{-x}+1=0$ .

Exercice 30 :

1)Résoudre dans $\mathbb{R}$ l’inéquation $e^{-x}-e^x>0$ .

2)En déduire le signe de $1-\frac{1+e^x}{1+e^{-x}}$ sur $\mathbb{R}$ .

Exercice 31 :

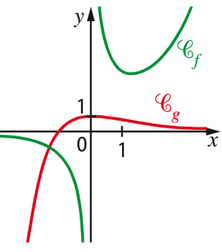
Soit f la fonction définie sur $\mathbb{R}^*$ par $f(x)=\frac{e^x+1}{x}$

et g la fonction définie sur $\mathbb{R}$ par $g(x)=\frac{x+1}{e^x}$ .

On donne ci-dessous les courbes représentatives C_f et C_g des fonctions f et g.

Conjecturer les limites des fonctions f et g aux bornes de leur ensemble de définition.
Démontrer ces conjectures.

Exercice 32 :

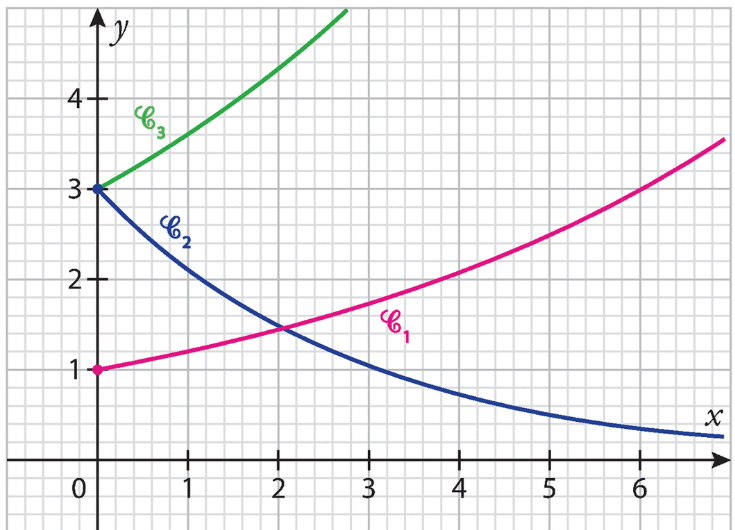
On considère les fonctions f, g et h dont les courbes sont tracées dans le repère ci-dessous.
Elles sont définies sur $\mathbb{R}^{+}$ par :

$f(x)=3\times \,0,7^x$
$g(x)=3\times \,1,2^x$
$h(x)\,=\,1,2^x$

Associer chaque fonction à sa courbe représentative.

Exercice 33 :

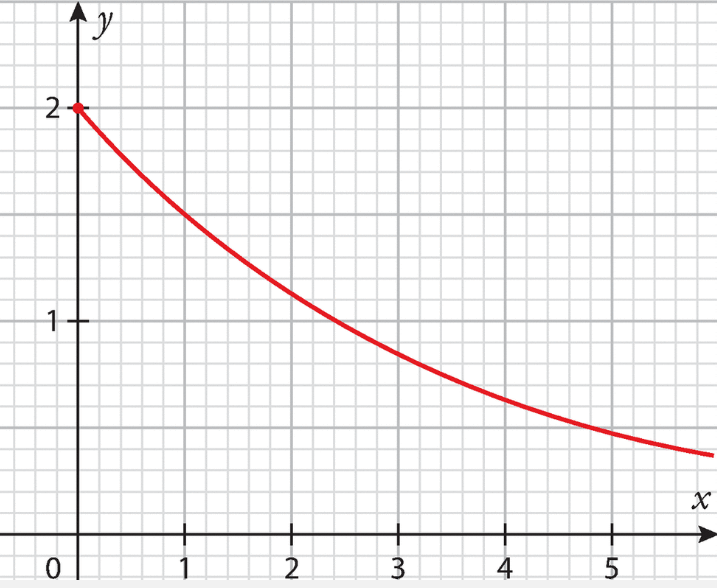
f est une fonction de la forme $x\,\mapsto \,k\times \,a^x$ , dont on donne la représentation graphique dans le repère
ci-dessous.

Déterminer les valeurs de k et de a.

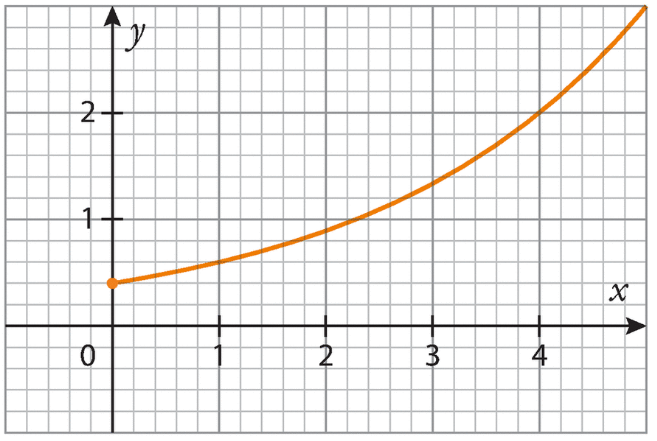
Exercice 34 :

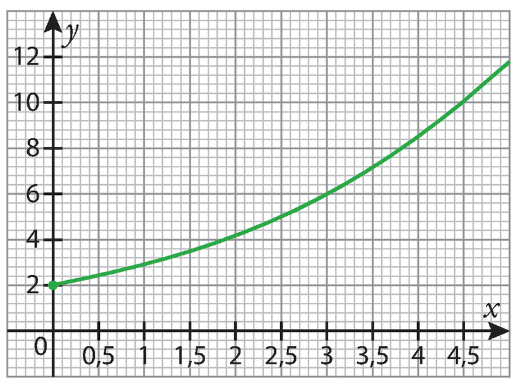
f est une fonction de la forme $x\,\mapsto \,k\times \,a^x$ , définie sur $\mathbb{R}^{+}$ .

Sa courbe représentative est donnée dans le repère ci-dessous.

1.Déterminer graphiquement f(0) et f(l ).
2.En déduire les valeurs de k et de a.

Exercice 35 :
Le nombre de bactéries d’un échantillon de laboratoire augmente de 50 % chaque jour.

On suppose que l’échantillon contient 2 000 bactéries le premier jour, et on note u(n) le nombre de bactéries (en milliers) présentes au bout de n jours.

Ainsi, $u(0)\,=\,2$ .
a) Donner la nature de la suite .
b) Donner le terme général de la suite .
c) En calculant les premiers termes de la suite, déterminer
au bout de combien de jours la population de bactérie dépassera 10 000.
2. On a représenté dans le graphique ci-dessous la courbe
de la fonction f définie sur $[0;+\infty[$ par $f(x)\,=\,2\,\times \,1,5^x$ .

a. En utilisant la courbe représentative de la fonction f, retrouver le résultat de la question 1 c).
b. Déterminer le nombre de bactéries au bout de 12 h.

5/5 - (21587 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonction exponentielle : exercices de maths en 1ère corrigés en PDF.» au format PDF.