Equations et second degré : corrigé des exercices de maths en 1ère en PDF.
Mis à jour le 14 septembre 2025
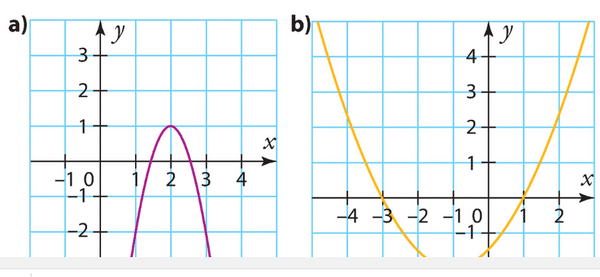
Exercice 1 :
a. 
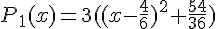
b. 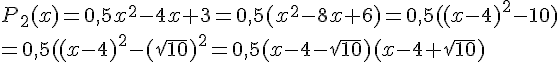
c. Poser 
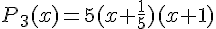
d. 
e. 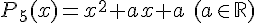
Il fait effectuer un raisonnement par disjonction des cas :
Si ![x\in [0;4] P_5(x)=(x+\frac{a}{2})^2-\frac{a(a-4)}{4}](https://mathovore.fr/latex-images/360c1745a9b9342615f8321829b19330.png)
Si ![x\not\in [0;4] P_5(x)=(x+\frac{a}{2}-\sqrt{\frac{a(a-4)}{4}})(x+\frac{a}{2}+\sqrt{\frac{a(a-4)}{4}})](https://mathovore.fr/latex-images/2e71d0fea0c1dfa7286c28052a04ff13.png)
Exercice 2 :
a. 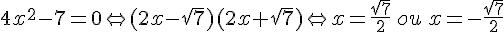
b. 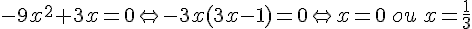
c. 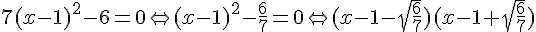
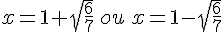
e. ![4(x-2)^2=9(2x+3)^2\Leftrightarrow [2(x-2)]^2-[3(2x+3)]^2=0\Leftrightarrow (4x-4-6x-9)(4x-4+6x+9)=0](https://mathovore.fr/latex-images/2a03a3c02579af70a1f26c9981a796f9.png)
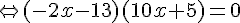

Exercice 3 :
1. 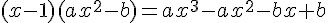
par identification a =2 et b= 1 .
2. 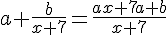
par identification a=4 et en résolvant l’équation 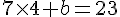
, nous obtenons b=19.
Exercice 4 :
a. 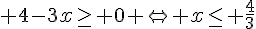
b. ![x\in ]-\infty ; -3[\cup]3;+\infty[](https://mathovore.fr/latex-images/f5dde42e5f5873f6eb3b6a63350eb5da.png)
c. Ensemble vide.
d. 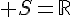
e. 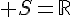
Exercice 5 :
a. 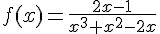 .
.
f est définie 
donc 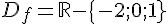
b. 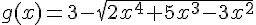
f est définie 
![\Leftrightarrow x\in ]-\infty;-3]\cup[\frac{1}{2};+\infty[](https://mathovore.fr/latex-images/0dbf54139349f718e454dc26fee82a35.png) .
.
Exercice 6 :
1. 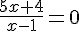 .
.

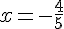
2. 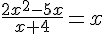 .
.
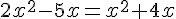
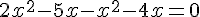
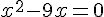
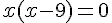

3. 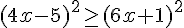 .
.

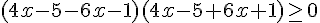

Les racines sont :

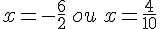
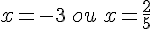
Conclusion : L’ensemble solution est ![[-3;\frac{2}{5}]](https://mathovore.fr/latex-images/04f17c27be4109abac33d5236e9d6c33.png) .
.
Exercice 7 :
Pour résoudre cette inéquation, nous allons suivre les étapes suivantes :
1. Trouver les valeurs pour lesquelles le numérateur est égal à zéro : 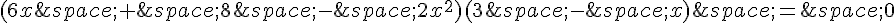
Le premier facteur est égal à zéro si 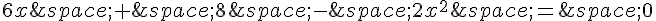
Réarrangeons l’équation :
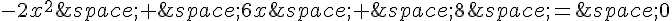
Nous pouvons diviser toute l’équation par -2 :
x^2 – 3x – 4 = 0
En factorisant, nous obtenons :
(x – 4)(x + 1) = 0
Cela donne les solutions : x = 4 et x = -1
Le deuxième facteur est égal à zéro si 3 – x = 0
Cela donne la solution x = 3
2. Trouver les valeurs pour lesquelles le dénominateur est égal à zéro : 4x^2 – 12x + 9 = 0
Pour résoudre cette équation quadratique, nous pouvons utiliser la formule quadratique ou la factorisation.
En utilisant la factorisation, nous obtenons :

Cela donne la solution x = 3/2
Ainsi, les valeurs critiques de x sont x = -1, x = 3/2, x = 3 et x = 4.
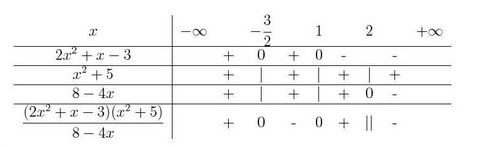
3. Construire un tableau de signes en utilisant les valeurs critiques :
\begin{array}{|c|c|c|c|c|} \hline & (-\infty,-1) & (-1,\frac{3}{2}) & (\frac{3}{2},3) & (3,4) & (4,+\infty) \\ \hline 6x+8-2x^2 & + & + & + & – & – \\ \hline 3-x & – & – & + & + & + \\ \hline 4x^2-12x+9 & + & – & + & + & + \\ \hline \frac{(6x+8-2x^2)(3-x)}{4x^2-12x+9} & – & + & – & + & – \\ \hline \end{array}
4. Identifier les intervalles pour lesquels l’expression est positive ou nulle.
L’expression est positive ou nulle sur les intervalles ![]1,\,\frac{3}{2}[](https://mathovore.fr/latex-images/118b814469b0b479813c3560177f41cb.png) et (3, 4].
et (3, 4].
Donc, la solution de l’inéquation est l’union de ces deux intervalles :
![x\,\in\,]-1,\,3/2[\,\cup\,[3,\,4]](https://mathovore.fr/latex-images/670e273327a86c82c4e6deec2b013cc4.png)
Exercice 8 :
1. Pour trouver une fonction polynôme du second degré ayant 1 et 4 comme racines, nous utilisons la forme factorisée du polynôme :
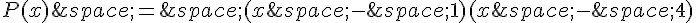
Si nous voulons que la courbe représentative de ce polynôme passe par le point A(-1, 1), nous substituons les coordonnées du point dans le polynôme :
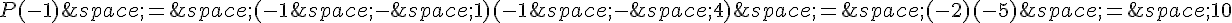
Cependant, nous voyons que P(-1) ne correspond pas à la valeur y = 1 donnée par le point A. Par conséquent, il n’existe pas de fonction polynôme du second degré ayant 1 et 4 comme racines et passant par le point A(-1, 1).
2. Nous devons montrer que pour tout réel a, l’équation 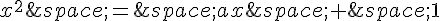 a deux solutions réelles distinctes.
a deux solutions réelles distinctes.
Pour cela, nous pouvons utiliser le discriminant de l’équation quadratique. Le discriminant est défini comme 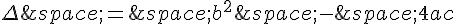 , où a, b et c sont les coefficients de l’équation.
, où a, b et c sont les coefficients de l’équation.
Dans ce cas, a = 1, b = -a et c = 1.
Donc, le discriminant est 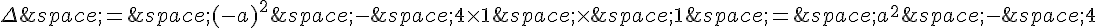 .
.
Pour que l’équation ait deux solutions réelles distinctes, le discriminant doit être strictement positif : 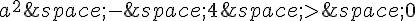 .
.
Cela implique que 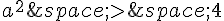 , donc |a| > 2.
, donc |a| > 2.
Donc, pour tout réel a dont la valeur absolue est supérieure à 2 (|a| > 2), l’équation x^2 = ax + 1 admet deux solutions réelles distinctes.
3. Pour que l’équation 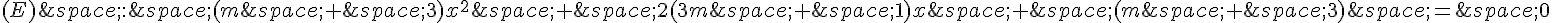 ait une unique solution, son discriminant doit être égal à zéro : b^2 – 4ac = 0.
ait une unique solution, son discriminant doit être égal à zéro : b^2 – 4ac = 0.
Dans ce cas, 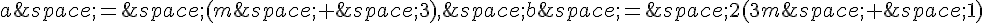 et c = (m + 3).
et c = (m + 3).
Donc, le discriminant est :
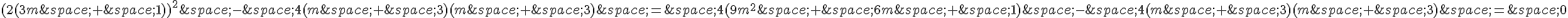
Nous pouvons simplifier cette équation en développant les termes :
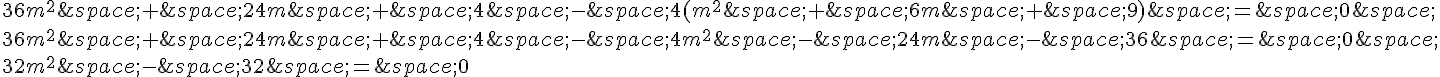
Divisons par 32 pour simplifier l’équation :

Cette équation peut être factorisée comme 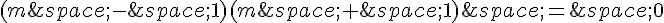 .
.
Donc, les valeurs de m pour lesquelles l’équation (E) a une unique solution sont m = 1 et m = -1.
Pour calculer la solution lorsque m = 1, nous substituons m dans l’équation :
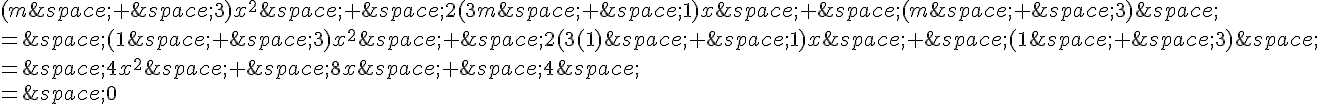
Nous pouvons diviser toute l’équation par 4 pour simplifier :

Cette équation peut être factorisée comme 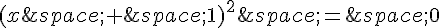 .
.
La solution unique est donc x = -1.
Exercice 9 :
Pour résoudre cette problématique, nous allons suivre les étapes suivantes :
1. Pour exprimer en fonction de x l’aire de la partie coloriée, on peut considérer deux parties distinctes : la bande coloriée et le carré central.
La bande coloriée a une largeur x cm et une longueur égale à la longueur du carré, c’est-à-dire 10 cm. Donc, l’aire de la bande est de 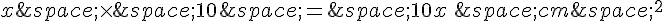 .
.
Le carré central a un côté de longueur x cm, donc son aire est de 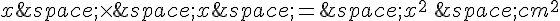 .
.
L’aire totale de la partie coloriée, notée A(x), est donc la somme de ces deux aires : 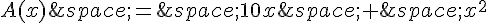 cm².
cm².
2. Pour trouver les valeurs de x pour lesquelles l’aire coloriée est égale à l’aire de la partie blanche, nous devons considérer que l’aire du carré total est de 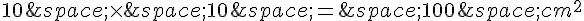 .
.
L’aire de la partie blanche est donc égale à l’aire totale moins l’aire de la partie coloriée : 100 cm² – A(x).
Nous devons donc résoudre l’équation suivante :
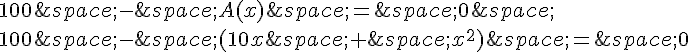
Réarrangeons cette équation :
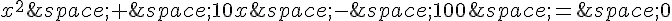
On peut résoudre cette équation quadratique en utilisant la formule quadratique ou en factorisant. Factorisons cette équation :
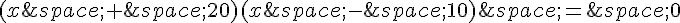
Cela donne deux solutions possibles : x = -20 ou x = 10.
Cependant, une valeur négative pour x n’a pas de sens dans ce problème, puisque x représente une longueur. Donc, la seule valeur valide pour x est x = 10.
Par conséquent, pour x = 10 cm, l’aire coloriée est égale à l’aire de la partie blanche.
Exercice 10 :
1. Pour résoudre l’équation 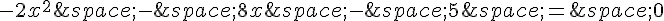 , nous pouvons utiliser la méthode du discriminant :
, nous pouvons utiliser la méthode du discriminant :
Le discriminant Δ est donné par 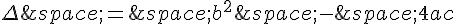 , où a = -2, b = -8 et c =
, où a = -2, b = -8 et c =
-5.
Calculons le discriminant : 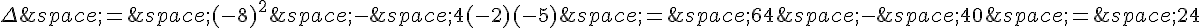 .
.
Puisque le discriminant est positif (Δ > 0), cela signifie que l’équation 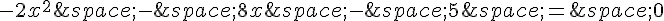 admet deux solutions réelles distinctes.
admet deux solutions réelles distinctes.
Nous pouvons utiliser la formule quadratique pour trouver les solutions :
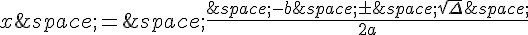

Simplifions :
x = (8 ± 2√6) / -4
x = (4 ± √6) / -2
Les solutions de cette équation sont donc x = -(4 + √6) / 2 et x = -(4 – √6) / 2.
2. Pour résoudre l’équation 9(1-x)^2 = 4(2x + 1)^2, nous devons développer les termes et simplifier l’équation :


Réarrangeons cette équation :


Nous pouvons essayer de factoriser cette équation pour trouver les solutions, mais dans ce cas, cela ne semble pas possible.
Nous pouvons utiliser la formule quadratique pour résoudre cette équation :
x = (-b ± √Δ) / (2a)
a = 25, b = -34 et c = 5.
Calculons le discriminant : 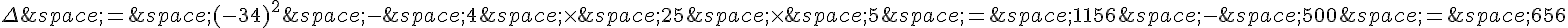 .
.
Le discriminant est positif, donc l’équation a deux solutions réelles distinctes.
Les solutions de cette équation sont donc :

Simplifions :
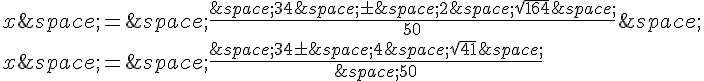
Finalement, les solutions de l’équation sont 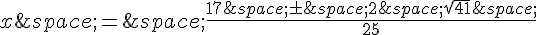 .
.
3. Pour résoudre l’équation fractionnelle, nous devons trouver un dénominateur commun et simplifier l’équation :

Pour avoir un dénominateur commun, nous multiplions 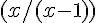 par (x-2) et
par (x-2) et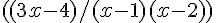 par (x-1) :
par (x-1) :
![[x(x-2)/(x-1)(x-2)]\,-\,[(3x-4)/(x-1)(x-2)]\,=\,0](https://mathovore.fr/latex-images/eef484d4ceb50de140515d78daabc65a.png)
Simplifions l’équation :
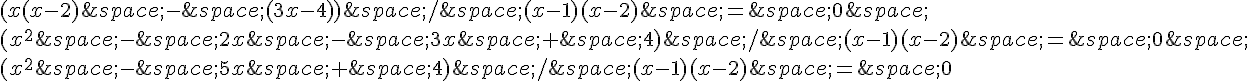
Nous pouvons maintenant factoriser le numérateur de l’équation pour résoudre :
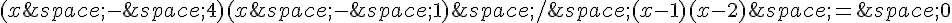
Maintenant, nous pouvons simplifier et trouver les solutions :
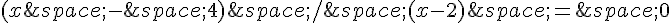
Le numérateur doit être égal à zéro pour que l’équation soit satisfaite :
x – 4 = 0
x = 4
La solution de l’équation est donc x = 4.
4. Pour résoudre l’inéquation 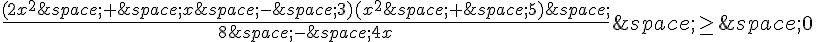 , nous devons trouver les valeurs de x qui satisfont cette inégalité.
, nous devons trouver les valeurs de x qui satisfont cette inégalité.
Pour cela, nous devons considérer les valeurs de x pour lesquelles l’expression est positive ou nulle. Nous devons donc trouver les zéros et les points de discontinuité de l’expression.
Tout d’abord, nous devons prendre en compte que le dénominateur ne peut pas être égal à zéro : 8 – 4x ≠ 0.
Cela signifie que x ≠ 2.
Ensuite, nous devons trouver les zéros de l’expression. Nous avons :
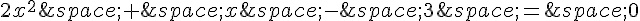
Nous pouvons résoudre cette équation en utilisant la formule quadratique :
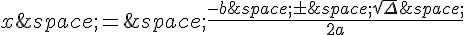
a = 2, b = 1 et c = -3.
Calculons le discriminant : 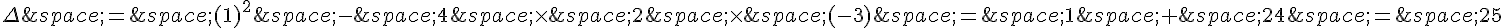 .
.
Le discriminant est positif, nous avons donc deux solutions réelles distinctes.
Les solutions de cette équation sont donc :

Simplifions :
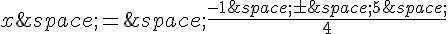
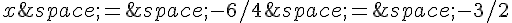 ou
ou 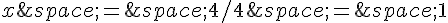 .
.
Maintenant, nous pouvons dresser un tableau de signes pour trouver les intervalles de x qui satisferont l’inégalité :
Donc, les solutions de l’inéquation sont les intervalles x ∈ (-∞, -3/2) ∪ (1, 2).
L’expression est positive ou nulle pour ces valeurs de x.
Exercice 11 :
L’aire d’un triangle rectangle est 429 m², et l’hypoténuse a pour longueur h = 72,5 m.
Trouver le périmètre.
Notons 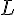 la longueur du triangle rectangle et sa largeur.
la longueur du triangle rectangle et sa largeur.
Nous avons 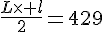 donc
donc 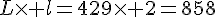 ainsi
ainsi 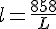
Remarque :  car l’aire du triangle rectangle est non null, donc nous pouvons diviser par L.
car l’aire du triangle rectangle est non null, donc nous pouvons diviser par L.
Appliquons le théorème de Pythagore à ce triangle rectangle :
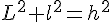

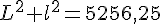


Multiplions cette équation par 
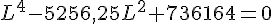
Posons 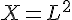 :
:
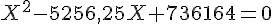
Calculons la valeur du discriminant :
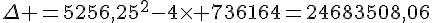
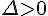 , il y a donc deux racines distinctes dans
, il y a donc deux racines distinctes dans 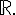

et
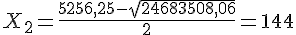
Nous obtenons donc 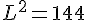 ou
ou 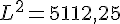
Comme L est une longueur alors L>0.
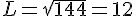 ou
ou 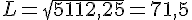
ce qui nous donnerait :
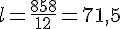 ou
ou 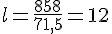
or la longueur est plus grande que la largeur.
La longueur du triangle rectangle est L = 71,5 m et la largeur est 12 m.
Conclusion : Son périmètre est 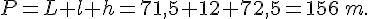
Exercice 12 :
Pour se rendre d’une ville A à une ville B distantes de 195 km, deux cyclistes partent en même temps.
L’un deux, dont la vitesse moyenne sur ce parcours est supérieure à 4 km/h à celle de l’autre, arrive une heure plus tôt.
Quelles sont les vitesses des deux cyclistes ?
Indication : Utiliser le fait que la vitesse moyenne v est 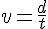
avec d la distance parcourue et t le temps écoulé.
Exercice 13 :
1. On dispose d’une baguette de bois de 10 cm de long.
Où briser la baguette pour que les morceaux obtenus soient deux côtés consécutifs d’un rectangle de surface 20 cm² ?
On note x la distance à laquelle on brise la baguette, on obtient un autre morceau de longueur 10 – x .
On doit avoir 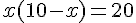

Calculons la valeur du discriminant :
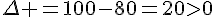 , il y a donc deux racines réelles distinctes.
, il y a donc deux racines réelles distinctes.
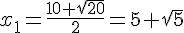 et
et 
Il faut donc couper la baguette exactement 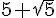 ce qui revient à couper à partir de l’autre bout
ce qui revient à couper à partir de l’autre bout 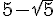 .
.
2. Même question avec un rectangle d’aire 40 cm².
Exactement le même principe, nous vous laissons faire…..![]()
Exercice 14 :
Résoudre les inéquations suivantes :
1. 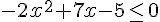
Calculons la valeur du discriminant :
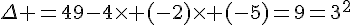
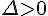 , il y a deux racines réelles distinctes.
, il y a deux racines réelles distinctes.
 et
et 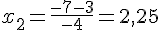
a est négatif donc ![{\color{DarkRed} S=]-\infty;1]\cup [2,25;+\infty[}](https://mathovore.fr/latex-images/c34ec60332cc783d88e19a9b5870821f.png) .
.
2. 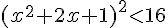
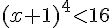





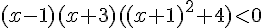
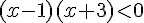 car
car 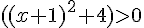
a est positif et les racines sont 1 et – 3.
![{\color{DarkRed} S=[-3;1]}](https://mathovore.fr/latex-images/e96cc03bab2d38cd5c4a5e4f98997060.png)
Exercice 15 :
1. Résoudre les équations suivantes :
a. 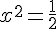 .
.
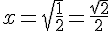 ou
ou 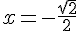
b. 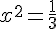 .
.
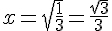 ou
ou 
2. Résoudre l’équation suivante : 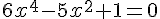 .
.
Posons 
on est amené à résoudre :

Calculons la valeur du discriminant :

Le discriminant est strictement positif, il existe donc deux racines réelles distinctes.
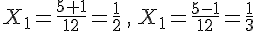
Nous avons donc :
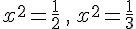
Ce sont les équations du 1.
Conclusion : 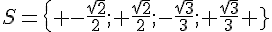
Exercice 16 :
Indication : faire un schéma puis utiliser les propriétés de la symétrie axiale ainsi que l’aire d’un trapèze.
Sur un drapeau rectangulaire de longueur 4 m et de largeur 3 m, on trouve une croix d’épaisseur x m.
Quelle valeur doit-on donner à la largeur de la croix pour que son aire soit égale à la moitié du drapeau ?
Exercice 17 :
1. 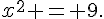

2. 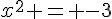 .
.
Impossible dans  , un carré est positif ou nul.
, un carré est positif ou nul.
3. 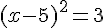 .
.


C’est une équation produit, il y a deux solutions :
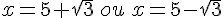
4. 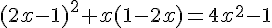 .
.
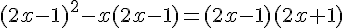
![(2x-1)[(2x-1)-x]-(2x-1)(2x+1)=0](https://mathovore.fr/latex-images/ff5872e4bfb7dd76fa2080765baaabba.png)
![(2x-1)[x-1]-(2x-1)(2x+1)=0](https://mathovore.fr/latex-images/21eefa10d26f36a485d946eb21ca5259.png)
![(2x-1)[x-1-(2x+1)]=0](https://mathovore.fr/latex-images/bdc33ca652b0b793c411cd5df4ad4d13.png)
![(2x-1)[x-1-2x-1]=0](https://mathovore.fr/latex-images/37424f9c7aff020fe8b1680f1b83fa1b.png)
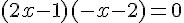
C’est une équation produit, il y a deux solutions :
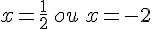
5) 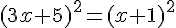 .
.
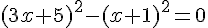
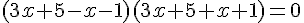
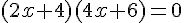
C’est une équation produit, il y a deux solutions :
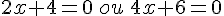

6) 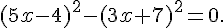
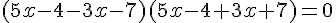
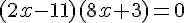
C’est une équation produit :
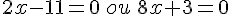

Exercice 18 :
Notons 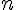 la longueur du plus petit carré .
la longueur du plus petit carré .
Nous avons :

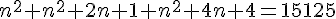
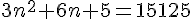
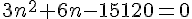
Calculons la valeur du discriminant :
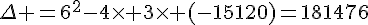
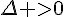 , il existe deux racines réelles distinctes.
, il existe deux racines réelles distinctes.
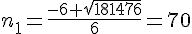 et
et 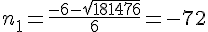
Or nous recherchons la longueur d’un côté donc un entier positif .
Conclusion : les longueurs de ces trois carrés sont 70, 71 et 72 .
Exercice 19 :
Nous obtenons l’équation suivante en traduisant l’égalité des deux aires :
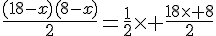
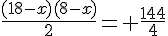
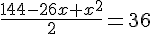
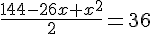
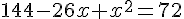
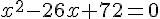
Calculons la valeur du discriminant :
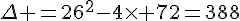
Le discriminant est strictement positif, il existe donc deux racines réelles distinctes.
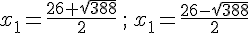
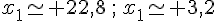
or ![D\in[AC]](https://mathovore.fr/latex-images/5b15bf9a290ef0e14cd34effdd447f32.png) donc
donc 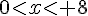
Conclusion : il faut que x prenne la valeur approximative de 3,2 mètres.
Exercice 20 :
Résoudre :
a. 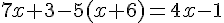
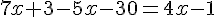
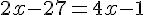

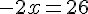

b. 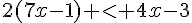

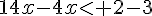
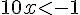

c. 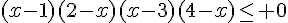
Exercice 21 :
Résoudre les équations suivantes :
1. 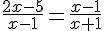
Utilisons le produit en croix :
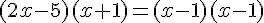
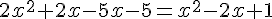

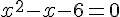
Une racine évidente est – 2 :
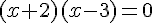
C’est une équation produit, il y a deux solutions :

2. 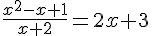

Utilisons le produit en croix :
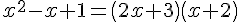
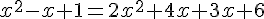

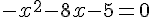
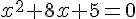
Calculons le discriminant :
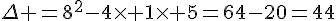
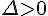 , il y a donc deux racines distinctes réelles .
, il y a donc deux racines distinctes réelles .
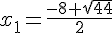 ou
ou 
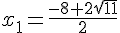 ou
ou 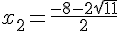
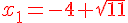 ou
ou 
Exercice 22 :
Quel était le prix d’essence à la première station et combien de litres en avait-on pris ?
Notons  le prix d’un litre d’essence dans la première station service en euro.
le prix d’un litre d’essence dans la première station service en euro.
Nous avons :
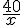 représente le nombre de litres d’essence achetés dans la première station.
représente le nombre de litres d’essence achetés dans la première station.
Dans la seconde on aurait pu avoir : 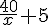 litres d’essence.
litres d’essence.
donc :

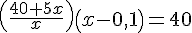
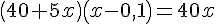

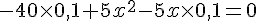
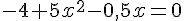
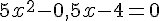
Calculons la valeur du discriminant :
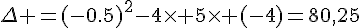
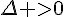 , il y a donc deux racines réelles distinctes .
, il y a donc deux racines réelles distinctes .
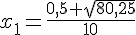 et
et 
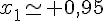 et
et 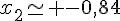
Conclusion : le prix étant positif, on en déduit que le prix d’un litre d’essence est de 0,95 € dans la première station.
on a prit 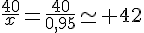 litres d’essence dans la première station et 47 dans la seconde .
litres d’essence dans la première station et 47 dans la seconde .
Exercice 23 :
Trouver deux nombres dont la somme est égale à 57 et le produit égal à 540.
Soit S la somme et P le produit de ces deux nombres.
Ces deux nombres sont solution de l’équation :

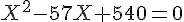
Calculons la valeur du discriminant :
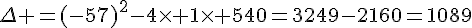
le discriminant est strictement positif, il y a deux solutions distinctes :
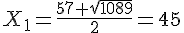 et
et 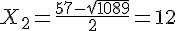
Conclusion : les deux nombres recherchés sont 45 et 12 .
Exercice 24 :
Résoudre l’inéquation suivante :
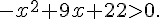
Calculons la valeur du discriminant :

Le discriminant est strictement positif, il existe deux racines réelles distinctes.
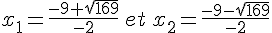
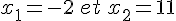
Le coefficient dominant a=-1<0 donc 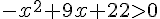 pour
pour ![x\in]-2;11[](https://mathovore.fr/latex-images/83161966b3e0945f17dd9de6a4f5e0f7.png)
1)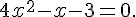
La valeur du discriminant es t 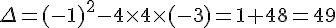 .
.
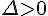 , il y a donc deux racines distinctes.
, il y a donc deux racines distinctes.
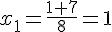 et
et 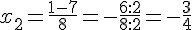
Conclusion : 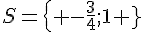
2) 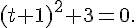

Un carré est toujours positif ou nul donc cette équation n’a pas de solution dans 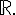
3) 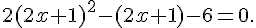

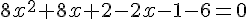

La valeur du discriminant est 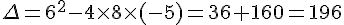 .
.
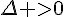 , il y a donc deux racines distinctes.
, il y a donc deux racines distinctes.
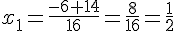 et
et 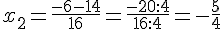
Conclusion : 
4) 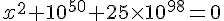 .
.
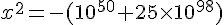
Le carré d’un nombre est toujours positif ou nul donc cette équation n’a pas de solution dans 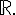
Exercice 25 :
1. On cherche les éventuelles racines de f, c’est-à-dire les valeurs de x pour lesquelles f(x) = 0 :
– -x² + 6x – 8 = 0
On peut résoudre cette équation du second degré en utilisant la formule :
– x = [-b ± √(b² – 4ac)] / 2a
En identifiant les coefficients, on a a=-1, b=6, c=-8. On peut alors remplacer dans la formule pour obtenir :
– x = (-(6) ± √((6)² – 4(-1)(-8))) / 2(-1)
On simplifie pour obtenir :
– x = 2 ± √6
Ainsi, les éventuelles racines de f sont x = 2 – √6 et x = 2 + √6.
On peut alors factoriser f(x) en utilisant les racines trouvées :
– f(x) = -(x – (2 – √6))(x – (2 + √6))
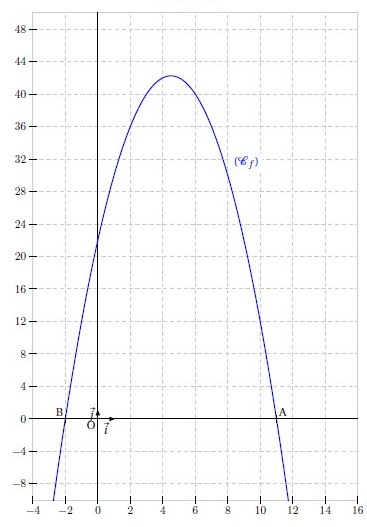
2. Pour déterminer les coordonnées des points d’intersection de la courbe de f avec les axes du repère, on cherche les valeurs de x pour lesquelles f(x) = 0 :
– f(x) = -x² + 6x – 8 = 0
On peut résoudre cette équation en utilisant la factorisation trouvée dans la question 1 :
– -(x – (2 – √6))(x – (2 + √6)) = 0
Ainsi, les solutions de l’équation sont x = 2 – √6 et x = 2 + √6.
Pour trouver les coordonnées des points d’intersection avec l’axe des x, on a y = 0 :
– Pour x = 2 – √6, on a f(2 – √6) = 0 – (2 – √6)² + 6(2 – √6) – 8 = -2√6
– Pour x = 2 + √6, on a f(2 + √6) = 0 – (2 + √6)² + 6(2 + √6) – 8 = 2√6
Ainsi, les coordonnées des points d’intersection sont :
– (2 – √6 ; 0) et (2 + √6 ; 0)
3. Pour étudier la position relative des courbes de f et g, on peut représenter les deux fonctions sur le même graphique :
<img src= »https://mathovore.fr/latexrender/pictures/f7d33088296fd407c9b06462eecf9fc2.png » align= »absmiddle » />
On peut alors remarquer que :
– g est une droite qui passe par le point (0 ; 3) et qui a une pente de -1 (car son coefficient directeur est -1).
– f est une parabole dont l’expression est -x² + 6x – 8.
On peut alors observer les trois situations suivantes :
– Si f est au-dessus de g sur tout l’intervalle considéré, alors f(x) > g(x) pour tout x, soit :
<img src= »https://mathovore.fr/latexrender/pictures/dee115b2c08b0a1503fb7dd587268949.png » align= »absmiddle » />
– Si f est en-dessous de g sur tout l’intervalle considéré, alors f(x) < g(x) pour tout x, soit :
<img src= »https://mathovore.fr/latexrender/pictures/c2454c454448ab155e767f12717c24b2.png » align= »absmiddle » />
– Si f coupe g en un point et est au-dessus de g à gauche de ce point et en-dessous à droite, alors :
<img src= »https://mathovore.fr/latexrender/pictures/2702d16e0ef55936186ee81fa304cfce.png » align= »absmiddle » />
En étudiant la courbe, on observe que f et g se coupent en un point d’abscisse x = 3. Ainsi, on a les informations suivantes :
– f est au-dessus de g sur l’intervalle ]-∞ ; 3[
– f est en-dessous de g sur l’intervalle ]3 ; +∞[
On peut alors résumer ces informations en disant que :
– f(x) > g(x) pour x ∈ ]-∞ ; 3[
– f(x) < g(x) pour x ∈ ]3 ; +∞[
Et que f et g se coupent en un point d’abscisse 3.
Exercice 26 :
1.
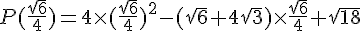
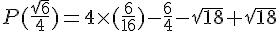
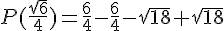
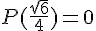
2.



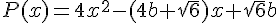
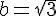
Conclusion : 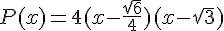
Exercice 27 :
Résoudre les équations suivantes :
a) 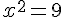

Il y a deux solutions .
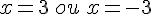
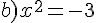
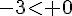
Il y a aucune solution car le carré d’un nombre est positif ou nul .
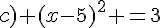
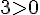
Il y a donc deux solutions
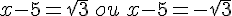
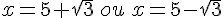
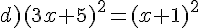
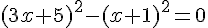
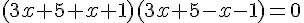

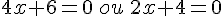


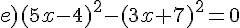

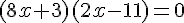

Exercice 28 :
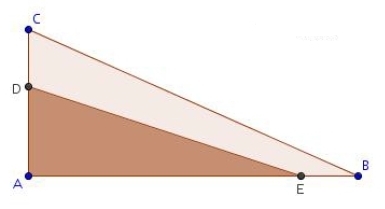
On sait que l’aire du triangle ABC est égale à
– (AB x AC) / 2 = (18 x 8) / 2 = 72 m²
On cherche à trouver x pour que l’aire du triangle ADE soit égale à la moitié de celle du triangle ABC, c’est-à-dire :
– (AE x AD) / 2 = 36 m²
On peut exprimer AE en fonction de x en utilisant le théorème de Pythagore dans le triangle ABE :
– AE² + BE² = AB²
– AE² + x² = 18²
– AE² = 18² – x²
De même, on peut exprimer AD en fonction de x en utilisant le théorème de Pythagore dans le triangle ADC :
– AD² + DC² = AC²
– AD² + (AC – AD)² = AC²
– AD² + (8 – AD)² = 8²
– AD² + 64 – 16AD + AD² = 64
– 2AD² – 16AD = 0
– AD² – 8AD = 0
– AD(AD – 8) = 0
Ainsi, on a AD = 8 ou AD = 0. On exclut la solution AD = 0, car dans ce cas le triangle ADE serait en fait une droite et son aire serait nulle. Ainsi, AD = 8.
On peut alors remplacer AE et AD par les expressions trouvées dans l’aire du triangle ADE pour obtenir une équation en x :
– (x x √(18² – x²)) / 2 = 36
– x x √(18² – x²) = 72
– x² (18² – x²) = 72²
– x^4 – 18² x² + 72² = 0
On peut résoudre cette équation du quatrième degré en remplaçant x² par y :
– y² – 18² y + 72² = 0
On peut résoudre cette équation du second degré en utilisant la formule :
– y = [18² ± √(18² – 4 x 72²)] / 2
– y = [18² ± √(18² – 20736)] / 2
– y = [18² ± √207360] / 2
– y = 81 ou y = 288
On retrouve alors les valeurs x = √81 = 9 et x = √288 ≈ 16,97 m.
On peut exclure la solution x = √81 = 9 m, car dans ce cas le point E se situe sur le coin du triangle ABC et le triangle ADE serait une droite et son aire serait nulle. Ainsi, la seule solution possible est x = √288 ≈ 16,97 m.
EXERCICE 29 :
1)a) En utilisant la formule du discriminant, on a :
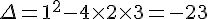
Comme  , l’équation n’a pas de solution réelle.
, l’équation n’a pas de solution réelle.
b) En utilisant la formule du discriminant, on a :
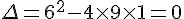
Comme 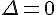 , l’équation a une solution réelle unique donnée par
, l’équation a une solution réelle unique donnée par 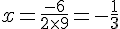 .
.
c) En factorisant, on obtient : 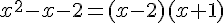 .
.
Les solutions de l’équation sont donc -1 et 2.
2) En utilisant la formule du discriminant, on a :  .
.
Comme 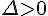 , l’équation a deux solutions réelles qui sont données par :
, l’équation a deux solutions réelles qui sont données par :
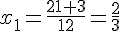 et
et 
EXERCICE 30 :
1)a) En utilisant la formule du discriminant, on a :
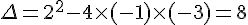
Comme 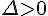 , la fonction a deux racines réelles données par :
, la fonction a deux racines réelles données par :
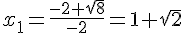 et
et 
b) En utilisant la formule du discriminant, on a :

Comme 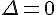 , la fonction a une racine réelle double donnée par :
, la fonction a une racine réelle double donnée par :
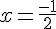
c) En utilisant la formule du discriminant, on a :

Comme \Delta > 0, la fonction a deux racines réelles données par :
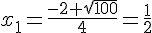 et
et 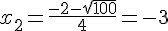 .
.
2) a) En utilisant la formule du discriminant, on a :
 .
.
Comme  , l’équation n’a pas de solution réelle.
, l’équation n’a pas de solution réelle.
b) En utilisant la formule du discriminant, on a :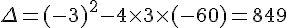 .
.
Comme 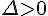 , l’équation a deux solutions réelles données par :
, l’équation a deux solutions réelles données par :
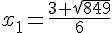 et
et 
c) En utilisant la formule du discriminant, on a :

Comme  , l’équation n’a pas de solution réelle.
, l’équation n’a pas de solution réelle.
EXERCICE 31 :
La fonction f est un polynôme de degré 2.
Pour déterminer le nombre de racines de la fonction, on calcule le discriminant : 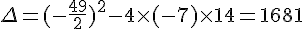 .
.
Comme 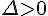 , la fonction a deux racines réelles distinctes.
, la fonction a deux racines réelles distinctes.
On vérifie que -4 est une racine en remplaçant x par -4 dans f(x) :

Donc -4 est bien une racine de f.
En utilisant la somme des racines, on a :
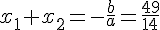
En utilisant le produit des racines, on a :
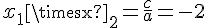 .
.
Les racines sont solutions de l’équations 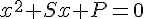 avec S la somme des deux racines et P leur produit.
avec S la somme des deux racines et P leur produit.
En résolvant ce système, on trouve que les deux racines sont -2 et 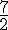 .
.
EXERCICE 32 :
a) La fonction f(x) est un polynôme de degré 2 car le terme de plus haut degré est 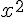 .
.
b) La fonction g(x) n’est pas un polynôme de degré 2 car elle contient une fraction.
c) La fonction h(x) n’est pas un polynôme de degré 2 car le terme de plus haut degré est x.
EXERCICE 33 :
1) En développant l’expression, on obtient :
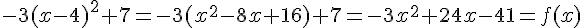
2) La forme canonique de f est de la forme 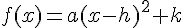 , où
, où 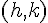 est le sommet de la parabole.
est le sommet de la parabole.
Pour obtenir cette forme, on complète le carré :

Donc la forme canonique de f est 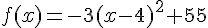 , et le sommet est (4,55).
, et le sommet est (4,55).
L’axe de symétrie est la droite verticale passant par le sommet.
Dans ce cas, c’est la droite x = 4.
Le signe de a est -3, donc la parabole est orientée vers le bas.
EXERCICE 34 :
a) La forme canonique de  est :
est :

Le sommet est 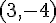 et l’axe de symétrie est la droite x = 3.
et l’axe de symétrie est la droite x = 3.
Le signe de a est 1, donc la parabole est orientée vers le haut.
b) La forme canonique de 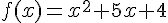 est :
est :
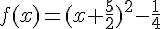
Le sommet est 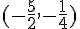 et l’axe de symétrie est la droite
et l’axe de symétrie est la droite 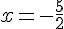 .
.
Le signe de a est 1, donc la parabole est orientée vers le haut.
EXERCICE 35 :
a) Les coordonnées du sommet sont 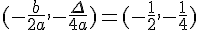 .
.
L’axe de symétrie est la droite 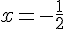 .
.
Le signe de a est 1, donc la parabole est orientée vers le haut.
b) Les coordonnées du sommet sont  .
.
L’axe de symétrie est la droite x = 1.
Le signe de a est 2, donc la parabole est orientée vers le haut.
c) Les coordonnées du sommet sont 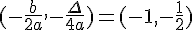 .
.
L’axe de symétrie est la droite x = -1.
Le signe de a est 2, donc la parabole est orientée vers le haut.
EXERCICE 36 :
a) L’axe de symétrie est la droite 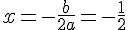 .
.
Les coordonnées du sommet sont 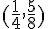 .
.
b) L’axe de symétrie est la droite 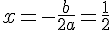 .
.
Les coordonnées du sommet sont 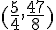 .
.
c) L’axe de symétrie est la droite 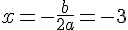 .
.
Les coordonnées du sommet sont (-3,-6).
d) L’axe de symétrie est la droite 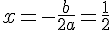 .
.
Les coordonnées du sommet sont 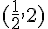 .
.
EXERCICE 37 :
a) On utilise l’identité remarquable 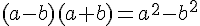 :
:

b) On utilise l’identité remarquable 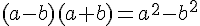 :
:
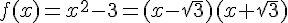
c) Pour factoriser 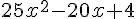 , on cherche deux nombres dont la somme est
, on cherche deux nombres dont la somme est 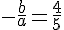 et le produit est
et le produit est 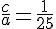 .
.
Ces nombres sont 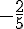 et
et 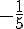 , donc :
, donc :
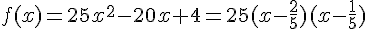
d) Pour factoriser 9x^2 + 24x + 16, on cherche deux nombres dont la somme est 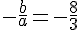 et le produit est
et le produit est  .
.
Ces racines doubles sont 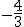 , donc :
, donc :
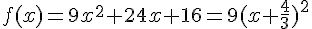
EXERCICE 38 :
a) Le discriminant est 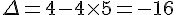 , donc l’équation n’a pas de solution réelle.
, donc l’équation n’a pas de solution réelle.
b) Le discriminant est 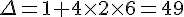 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
c) Le discriminant est  , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
d) Le discriminant est 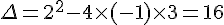 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
EXERCICE 39 :
a) On peut factoriser le trinôme par 3 : 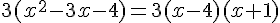 .
.
Donc les solutions sont x = 4 et x = -1.
b) Le discriminant est 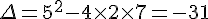 , donc l’équation n’a pas de solution réelle.
, donc l’équation n’a pas de solution réelle.
c) Le discriminant est 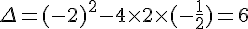 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
EXERCICE 40 :
a) On factorise le trinôme : 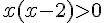 .
.
Les solutions sont donc : x < 0 ou x > 2.
b) Le trinôme est déjà factorisé : 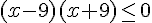 .
.
Les solutions sont 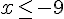 ou
ou 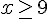 .
.
c) On trouve les racines du trinôme comme ceci : 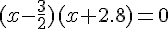 .
.
Les racines sont donc 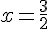 et
et  .
.
Il faut maintenant déterminer le signe de la fonction pour les intervalles suivants :![]-\infty,-2.8[,]-2.8,\frac{3}{2}[](https://mathovore.fr/latex-images/e0d10d1baeadc31951c51b8861771df1.png) et
et ![]\frac{3}{2},+\infty[](https://mathovore.fr/latex-images/bdd055dfc7d8890f80bb14200b8f2df9.png) .
.
On peut utiliser le test de signe ou la forme canonique de la fonction.
La forme canonique est 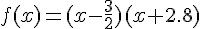 , donc on voit que la parabole est orientée vers le haut
, donc on voit que la parabole est orientée vers le haut 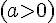 , et que les racines divisent le plan en deux intervalles.
, et que les racines divisent le plan en deux intervalles.
Donc le signe de la fonction est positif sur 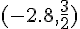 .
.
d) Le trinôme est déjà factorisé : 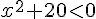 .
.
Comme  , la parabole est orientée vers le haut et n’a pas de racines réelles.
, la parabole est orientée vers le haut et n’a pas de racines réelles.
Donc la fonction est négative pour tout x réel.
EXERCICE 41 :
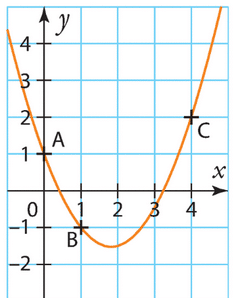
1. Le point A est sur la courbe de f, donc  .
.
En utilisant les coordonnées du point A, on a :
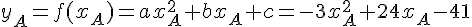
On peut utiliser les deux autres points pour écrire un système d’équations.
On utilise la méthode de substitution :
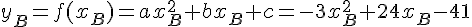
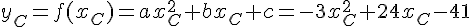
On peut résoudre ce système en soustrayant l’équation du point B à l’équation du point A, ce qui élimine le terme en c :
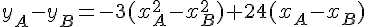
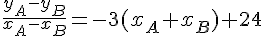
On peut ensuite soustraire l’équation du point C à l’équation du point A, ce qui permet d’éliminer le terme en 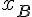 :
:


On a ainsi deux équations linéaires à deux inconnues : 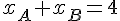 et
et 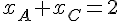 .
.
En les soustrayant, on trouve 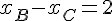 .
.
On peut ensuite utiliser cette équation pour exprimer 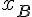 en fonction de
en fonction de 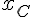 et simplifier les deux autres équations pour trouver les valeurs de a, b et c :
et simplifier les deux autres équations pour trouver les valeurs de a, b et c :
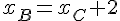


En substituant ces expressions dans les équations obtenues plus tôt, on trouve que 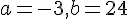 et
et 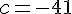 .
.
Donc l’expression de f est 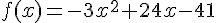 .
.
EXERCICE 42 :
a) Le discriminant est 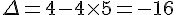 , donc l’équation n’a pas de solution réelle.
, donc l’équation n’a pas de solution réelle.
b) Le discriminant est 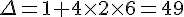 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
c) Le discriminant est  , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
d) Le discriminant est 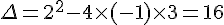 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
EXERCICE 43 :
a) Le discriminant est 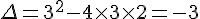 , donc l’équation n’a pas de solution réelle.
, donc l’équation n’a pas de solution réelle.
b) Le discriminant est 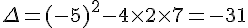 , donc l’équation n’a pas de solution réelle.
, donc l’équation n’a pas de solution réelle.
c) Le discriminant est 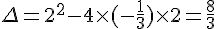 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
d) Le discriminant est 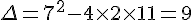 , donc l’équation a deux solutions réelles.
, donc l’équation a deux solutions réelles.
EXERCICE 44 :
a) Le sommet est sur l’axe des x, donc 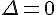 .
.
b) Le sommet est en dessous de l’axe des x, donc 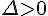 .
.
c) Le sommet est au dessus de l’axe des x, donc  .
.
d) Le sommet est au dessus de l’axe des x, donc  .
.
EXERCICE 45 :
a) On trouve les racines du trinôme :  .
.
On peut en déduire le tableau de signes :
x | -∞ | 2 | 4 | +∞ —|—-|—|—|—-
f(x) | – | 0 | + | +
b) On trouve les racines du trinôme :
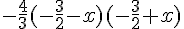 .
.
On peut en déduire le tableau de signes :
x | -∞ | 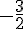 |
| 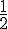 | +∞
| +∞
—|—-|———–|———|—-
f(x) | + | 0 | – | – c)
On trouve les racines du trinôme :
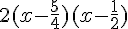 .
.
On peut en déduire le tableau de signes :
x | -∞ | 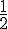 |
|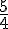 | +∞
| +∞
—|—-|———–|———–|—-
f(x) | – | + | – | –
EXERCICE 46 :
a) On factorise le trinôme : 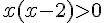 .
.
Les racines sont 0 et 2, donc il y a deux intervalles à considérer : ![]-\infty;0[](https://mathovore.fr/latex-images/e20c8052ee231e864e919e3183c8da8d.png) et
et ![]0;2[](https://mathovore.fr/latex-images/75c78f0d32b456d503131a7734b5f04a.png) .
.
On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.
On trouve que la fonction est positive sur ![]0;2[](https://mathovore.fr/latex-images/75c78f0d32b456d503131a7734b5f04a.png) et négative sur
et négative sur ![]-\infty;0[](https://mathovore.fr/latex-images/e20c8052ee231e864e919e3183c8da8d.png) et
et ![]2;+\infty[](https://mathovore.fr/latex-images/6199f041896ede3c58ba97b10f542e1b.png) .
.
Donc les solutions sont 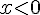 ou
ou 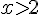 .
.
b) On trouve les racines du trinôme : 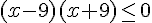 .
.
Les racines sont -9 et 9, donc il y a trois intervalles à considérer : ![]-\infty;-9]](https://mathovore.fr/latex-images/099e0d3dde172b902721110d8053de29.png) ,
, ![[-9,9]](https://mathovore.fr/latex-images/0bf95cd59de19d04a6d5bb0a0ed8b8b1.png) et
et 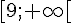 .
.
On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.
On trouve que la fonction est négative sur ![[-9,9]](https://mathovore.fr/latex-images/0bf95cd59de19d04a6d5bb0a0ed8b8b1.png) et positive sur
et positive sur ![]-\infty;-9]](https://mathovore.fr/latex-images/099e0d3dde172b902721110d8053de29.png) et
et 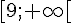 .
.
Donc les solutions sont 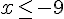 ou
ou 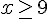 .
.
c) On trouve les racines du trinôme :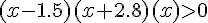 .
.
Les racines sont 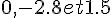 , donc il y a quatre intervalles à considérer :
, donc il y a quatre intervalles à considérer :
![]-\infty,-2,8[,]-2,8,0[,]0,1,5[](https://mathovore.fr/latex-images/95a9f7d1b5c73dbcbe7de0da4e529b56.png) et
et![]1,5;+\infty[](https://mathovore.fr/latex-images/ebaf198dbc52cf09e42d9bc3fd1f80cf.png) .
.
On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.
On trouve que la fonction est négative sur ![]-2.8,0[](https://mathovore.fr/latex-images/e406b283ce656b4d66ab7ceca8c811a8.png) et positive sur
et positive sur ![]-\infty,-2.8[,]0,1,5[](https://mathovore.fr/latex-images/9cbcc462444afe5a69346485b5995ed6.png) et
et ![]1,5,+\infty[](https://mathovore.fr/latex-images/cd8c2dc0d5045617c6f4c7a18d568849.png) . Donc les solutions sont
. Donc les solutions sont 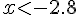 ou
ou ![x\in]0,1,5[](https://mathovore.fr/latex-images/f3990dfb6b606bf81ade3f8b9219fa28.png) .
.
d) Le trinôme est déjà factorisé : 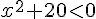 .
.
Comme  , la parabole est orientée vers le haut et n’a pas de racines réelles.
, la parabole est orientée vers le haut et n’a pas de racines réelles.
Donc la fonction est négative pour tout x réel.
Donc la solution est l’ensemble vide.
EXERCICE 47 :
a) On commence par résoudre l’équation associée 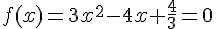 .
.
On calcule le discriminant : 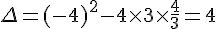 .
.
Le trinôme a donc deux solutions réelles.
En étudiant le signe de f(x) pour les intervalles ![]-\infty,\frac{1}{2}]](https://mathovore.fr/latex-images/e0ee09b11abfc33f60c55b5468a22260.png) ,
, 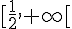 , on trouve que la solution est
, on trouve que la solution est ![x\in[\frac{1}{2},1]](https://mathovore.fr/latex-images/5014cc0e0d41f3c1b3294f145ad99e9b.png) .
.
b) On commence par résoudre l’équation associée 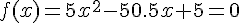 .
.
On calcule le discriminant : 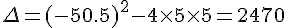 .
.
Le trinôme a donc deux solutions réelles.
En étudiant le signe de f(x) pour les intervalles ![]-\infty,\frac{1}{2}[](https://mathovore.fr/latex-images/779151af7ba247700084eda08a184c9d.png) ,
, ![]\frac{1}{2},+\infty[](https://mathovore.fr/latex-images/19620803c56c9fb148fabdd68b93d18c.png) ,
,
on trouve que la solution est ![x\in]\frac{1}{10},\frac{1}{2}[](https://mathovore.fr/latex-images/f3925aa21f178f7bd9227f79a49f150e.png) .
.
c) La parabole est orientée vers le haut, donc 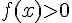 pour tout x.
pour tout x.
Donc la solution est l’ensemble  .
.
d) On commence par résoudre l’équation associée 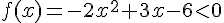 .
.
On calcule les racines du trinôme : 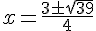 .
.
On peut alors dresser le tableau de signes de f(x) :
x | -∞ | 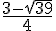 |
| 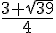 | +∞
| +∞
—|—-|———————–|—————-
EXERCICE 48 :
1. On complète le carré : 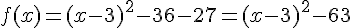 .
.
Donc la forme canonique de f est 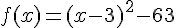 , et le sommet est
, et le sommet est 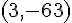 .
.
L’axe de symétrie est la droite verticale passant par le sommet.
Dans ce cas, c’est la droite 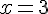 .
.
Le signe de a est 1, donc la parabole est orientée vers le haut.
2. On peut factoriser f(x) comme suit :

3.
a) On résout 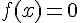 en utilisant la forme factorisée :
en utilisant la forme factorisée :

Les solutions sont 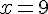 et
et 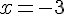 .
.
b) On résout f(x) = -27 en utilisant la forme factorisée :
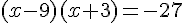
On peut réécrire -27 comme 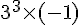 , et on utilise cette astuce pour factoriser :
, et on utilise cette astuce pour factoriser :

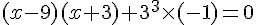
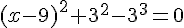
En utilisant la forme canonique, on voit que le sommet de la parabole est à 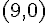 , et que la distance entre le sommet et l’axe des x est de 3.
, et que la distance entre le sommet et l’axe des x est de 3.
Donc les racines sont à une distance de 3 de l’axe des x, et se trouvent donc à 6 et 12 :
 ou
ou 
c) On résout  en utilisant la forme factorisée :
en utilisant la forme factorisée :
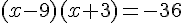
On peut réécrire 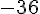 comme
comme 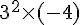 , et on utilise cette astuce pour factoriser :
, et on utilise cette astuce pour factoriser :
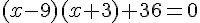
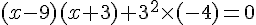
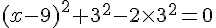
Là encore, on retrouve une équation de la forme 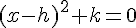 , donc la seule solution est
, donc la seule solution est 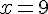 .
.
4.
a) On vérifie que 1 est racine en remplaçant x par 1 dans g(x) :

Donc 1 est bien racine de g.
b) En utilisant le produit et la somme des racines, on sait que :
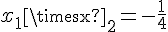 et
et 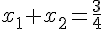
On sait aussi que x_1 = 1. On peut utiliser ces informations pour déterminer la valeur de x_2 :
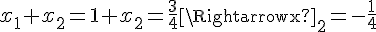
Donc les racines de g sont 1 et 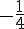 .
.
5. Pour résoudre f(x) < g(x), on peut d’abord réécrire les deux fonctions sous forme canonique :
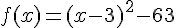

En soustrayant les deux fonctions, on trouve :

On veut maintenant trouver les valeurs x pour lesquelles 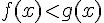 , c’est-à-dire les valeurs pour lesquelles.
, c’est-à-dire les valeurs pour lesquelles.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «equations et second degré : corrigé des exercices de maths en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
Exercices de première
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.