Limites de fonctions : corrigé des exercices de maths en 1ère en PDF.
Mis à jour le 16 septembre 2025
Exercice 1 :
Déterminer dans chaque cas 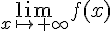 .
.
1. 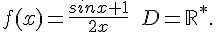
Il n’y a pas de forme indéterminée.
En  , le numérateur est majoré par 2 et minoré par 0 et le dénominateur tend vers
, le numérateur est majoré par 2 et minoré par 0 et le dénominateur tend vers 
donc 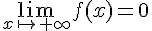
2. 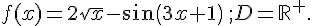
Il n’y a pas de forme indéterminée ici le sinus est borné entre – 1 et + 1
donc 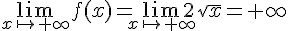
Exercice 2 :
Déterminer le domaine de définition D de f puis étudier les limites de f aux bornes de D.
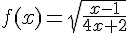
Il faut que 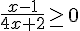 et
et 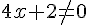
ce qui revient à 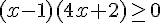 et
et 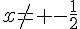
Conclusion : ![D_f=]-\infty;-\frac{1}{2}[\cup [1;+\infty[](https://mathovore.fr/latex-images/20b5937deb12a52fcca585878c55eae6.png)
Exercice 3 :
Déterminer la limite en  et
et 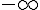 de :
de :
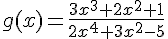
C’est une fonction rationnelle donc la limite en l’infini correspond au quotient des limites en plus l’infini des termes de plus haut degré.
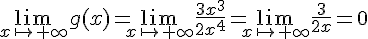
et de même :
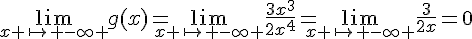
Exercice 4 :
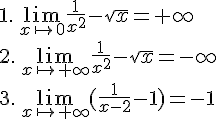
Exercice 5 :
1. La fonction 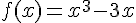 est dérivable sur
est dérivable sur  , et sa dérivée est :
, et sa dérivée est :
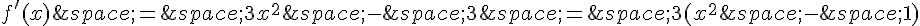
On résout l’équation 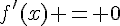 :
:
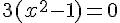
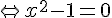
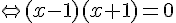
Ainsi, les solutions de l’équation 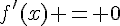 sont
sont 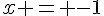 et
et 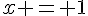 .
.
2. Pour qu’une tangente à la courbe  soit horizontale, il faut que sa pente (c’est-à-dire la valeur de sa dérivée) soit nulle. Ainsi, les coordonnées des points d’intersection de la courbe avec les tangentes horizontales sont les solutions de l’équation
soit horizontale, il faut que sa pente (c’est-à-dire la valeur de sa dérivée) soit nulle. Ainsi, les coordonnées des points d’intersection de la courbe avec les tangentes horizontales sont les solutions de l’équation 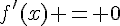 , c’est-à-dire les points de coordonnées
, c’est-à-dire les points de coordonnées 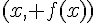 où
où 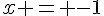 ou
ou 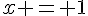 . Ces points sont donc
. Ces points sont donc 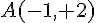 et
et 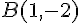 .
.
3. Les points d’intersection entre  et l’axe des abscisses sont les solutions de l’équation
et l’axe des abscisses sont les solutions de l’équation 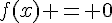 . On a :
. On a :
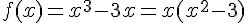
Ainsi, les solutions de l’équation 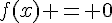 sont
sont 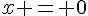 ,
, 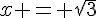 et
et 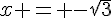 . Les coordonnées de ces points sont donc
. Les coordonnées de ces points sont donc 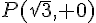 ,
, 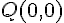 et
et 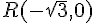 .
.
4. On veut l’équation de la tangente à  en
en 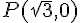 . La pente de cette tangente est donnée par la dérivée de
. La pente de cette tangente est donnée par la dérivée de  en
en 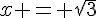 , c’est-à-dire :
, c’est-à-dire :
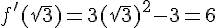
Ainsi, l’équation de la tangente en 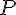 est de la forme
est de la forme 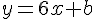 . Comme la tangente passe par le point
. Comme la tangente passe par le point 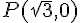 , on a :
, on a :
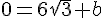
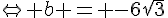
L’équation de la tangente en 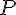 est donc :
est donc :
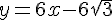
Exercice 6 :
1. Pour étudier les limites de 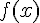 , on peut utiliser la forme indéterminée
, on peut utiliser la forme indéterminée 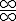 (pour la limite en
(pour la limite en  ) et la forme indéterminée
) et la forme indéterminée 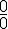 (pour la limite en
(pour la limite en 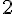 ). On a :
). On a :
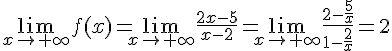
On a utilisé ici la règle de de L’Hôpital (en faisant tendre le numérateur et le dénominateur vers l’infini).
Pour la limite en 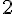 , on a :
, on a :
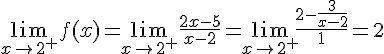
La limite en 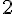 du côté droit est donc égale à
du côté droit est donc égale à 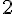 .
.
2. On calcule la dérivée de  en utilisant la formule du quotient (
en utilisant la formule du quotient (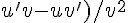 ) :
) :
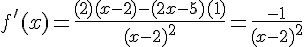
La dérivée 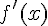 est donc strictement négative pour tout
est donc strictement négative pour tout 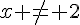 . En effet, le dénominateur est toujours positif, et le numérateur est négatif, donc la fraction est négative.
. En effet, le dénominateur est toujours positif, et le numérateur est négatif, donc la fraction est négative.
Exercice 7 :
Déterminer les limites suivantes :
1. 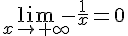
2. 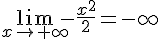
3. 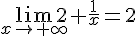
4. 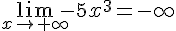
Exercice 8 :
1. 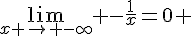
2. 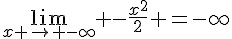
3. 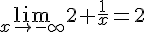
4. 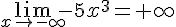
5. 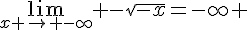
6. 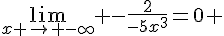
Exercice 9 :
1. 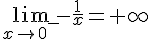
2. 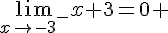
3. 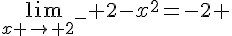
4. 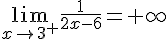
5. 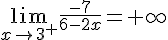
Exercice 10 :
Déterminer les limites de sommes ou de différences suivantes :
1. 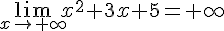
2. 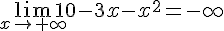
3. 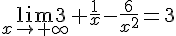
Exercice 11 :
Déterminer les limites de quotients et racines carrées suivantes :
1. 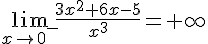
2. 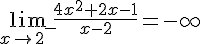
3. 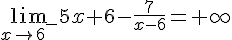
4. 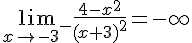
5. 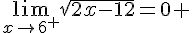
6. 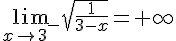
7. Elle n’existe pas.
Exercice 12 :
Préciser la limite des formes indéterminées suivantes :
1. 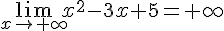
2. 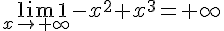
3. 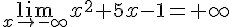
4. 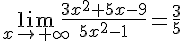
5. 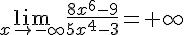
6. 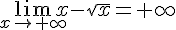
7. 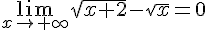
8. 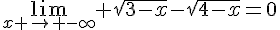
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «limites de fonctions : corrigé des exercices de maths en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.







