Angles orientés et repérage polaire : cours de maths en 1ère S.

Les angles orientés et le repérage polaire à travers un cours de maths en 1ère. Nous aborderons dans cette leçon en première, le sinus, le cosinus et la tangente avec les différentes relations trigonométriques.

I. Repérage sur le cercle trigonométrique.

1.Enroulement sur la droite numérique.

Définition: cercle trigonométrique.

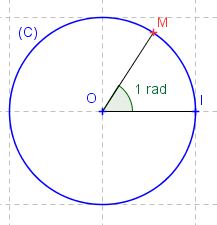
Le cercle trigonométrique $\varphi$ est le cercle de centre O et de rayon 1.

Il est muni d’un sens de parcours appelé sens direct, qui est l’inverse de celui des aiguilles d’une montre.

Avec ce choix, on dit que le plan est orienté.

Propriété :

Tout nombre réel a un point-image unique sur le cercle $\varphi$ .S’il existe $k\in\,\mathbb{Z}$ tel que $x'=x+2k\pi$ , alors et ont le même point-image sur le cercle $\varphi$ .

2.Le radian

Définition :

La mesure en radian d’un angle est égale à la longueur de l’arc du cercle trigonométrique qu’il intercepte.

Propriété :

Les mesures des angles en radian et en degré sont proportionnelles.

II. Mesures d’un angle orienté.

Définition : angle orienté.

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls et les points M et N tels que $\vec{OM}$ et $\vec{ON}$ sont leurs représentants respectifs d’origine O. Soient M’ et N’ les points d’intersection des demi-droites [OM) et [ON) avec le cercle trigonométrique.

Soient x et y deux nombres réels qui ont pour points-images M’ et N’, alors y-x est une mesure en radian de l’angle orienté $(\vec{u};\vec{v})$ .

Propriété : mesure principale.

L’angle orienté $(\vec{u};\vec{v})$ a une unique mesure $\alpha$ dans l’intervalle $]-\pi:\pi[$ appelée mesure principale de l’angle.

Propriétés :

Relation de Chasles pour les angles : soient $\vec{u}$ , $\vec{v}$ et $\vec{w}$ trois vecteurs non nuls, alors $(\vec{u},\vec{v})+(\vec{v},\vec{w})=(\vec{u},\vec{w})$ .
Caractérisation de la colinéarité de deux vecteurs : deux vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires si, et seulement si, $(\vec{u},\vec{v})=0[\pi]$ .

Propriétés :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls.

$(\vec{v},\vec{u})=-(\vec{u},\vec{v})$ ;
$(-\vec{u},-\vec{v})=\,(\vec{u},\vec{v})$
$(-\vec{u},\vec{v})=\,(\vec{u},\vec{v})[\pi]$
$(\vec{u},-\vec{v})=\,(\vec{u},\vec{v})[\pi]$

III. Cosinus et sinus d’un réel et d’un angle orienté.

1. Repérage à l’aide du cosinus et du sinus.

Théorème : coordonnées d’un point du cercle trigonométrique.

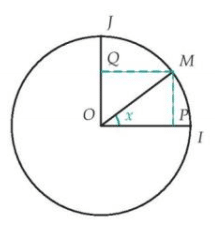
soit x un nombre réel et M son point-image sur le cercle trigonométrique $\varphi$ .Le point M a pour coordonnées .

Propriétés :

Pour tout réel x et pour tout entier relatif k.

(théorème de Pythagore).
$-1\leq\,\,cosx\leq\,\,1$
$-1\leq\,\,sinx\leq\,\,1$
$cos(x+2k\pi)=cosx$
$sin(x+2k\pi)=sinx$

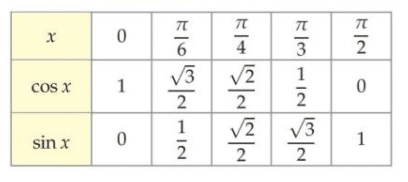
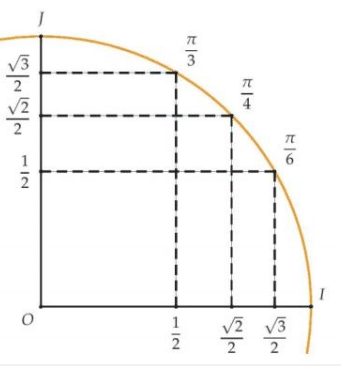
Les valeurs particulières :

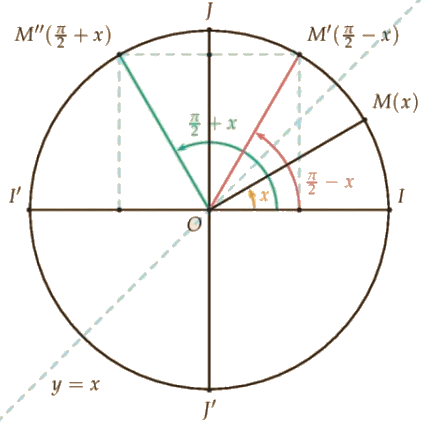
2. Les angles associés.

Propriétés :

Pour tout nombre réel x :

$cos(\pi-x)=-cosx$
$sin(\pi-x)=sinx$
$cos(\pi+x)=-cosx$
$sin(\pi+x)=-sinx$

Propriétés :

Pour tout nombre réel x :

$cos(\frac{\pi}{2}-x)=sinx$ .
$sin(\frac{\pi}{2}-x)=cosx$ .
$cos(\frac{\pi}{2}+x)=-sinx$ .
$sin(\frac{\pi}{2}+x)=cosx$ .

3. Formules de duplication.

Propriétés :

On considère deux nombres réels a et b.

$cos(a+b)=cosa\times \,cosb-sina\times \,sinb$ .
$cos(a-b)=cosa\times \,cosb+sina\times \,sinb$ .
$sin(a+b)=sina\times \,cosb+cosa\times \,sinb$ .
$sin(a-b)=sina\times \,cosb-cosa\times \,sinb$ .

Propriétés :

On considère un nombre réel a.

$cos(2a)=cos^2\,a-sin^2\,a\\=2cos^2\,a-1\\=1-2sin^2\,a$ .
$sin2a=2\times \,cosa\times \,sina$ .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «angles orientés et repérage polaire : cours de maths en 1ère en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.