Trigonométrie : corrigé des exercices de maths en 1ère en PDF.
Mis à jour le 16 septembre 2025
Exercice 1 :
Résoudre dans ![]-\pi;\pi]](https://mathovore.fr/latex-images/a693574a43f0291195eadc5321437c55.png) les équations suivantes.
les équations suivantes.
1. 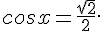
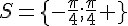
2. 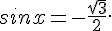
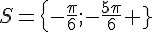
Exercice 2 :
Dans cet exercice, on donne :
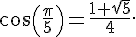
Calculer la valeur exacte de 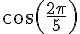 puis de
puis de 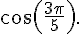
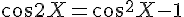
donc
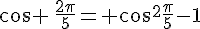
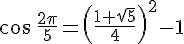
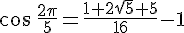
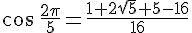
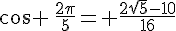
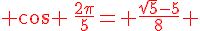
Indication : pour 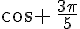 , utiliser la formule d’addition
, utiliser la formule d’addition 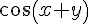 avec
avec 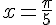 et
et 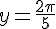 .
.
Exercice 3 :
Dans cet exercice, on dispose de la donnée suivante : 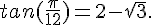
1. Soit ![x\in]0;\frac{\pi}{2}[](https://mathovore.fr/latex-images/3ba7f8e0d60593ccc8536568a099b8b6.png) . Démontrer que
. Démontrer que 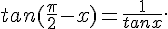

2. En déduire que :
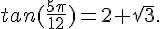
Utiliser l’égalité du 1. en prenant 
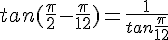
donc 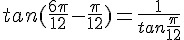
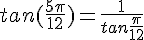
et en utilisant la donnée de l’énoncé :
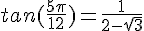
Multiplions par la quantité conjuguée et utilisons l’identité remarquable 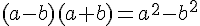 .
.
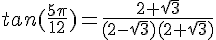
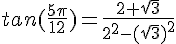
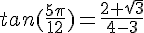
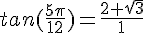
Conclusion : 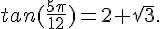
Exercice 4 :
Résoudre dans![]-\pi;\pi]](https://mathovore.fr/latex-images/a693574a43f0291195eadc5321437c55.png) l’équation : sin(2x) = cos(x).
l’équation : sin(2x) = cos(x).
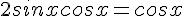
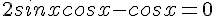
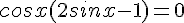
C’est une équation produit.
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
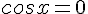 ou
ou 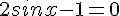
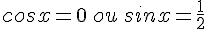
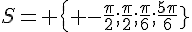
Exercice 5 :
Résoudre dans![]-\pi;\pi[](https://mathovore.fr/latex-images/59c37f95ad044b68700e6f5fe7148321.png) les équations suivantes :
les équations suivantes :
Indication : faire des changements de variable et utiliser les formules trigonométriques.
Pour la 1, poser X=cosx.
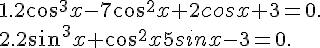
Exercice 6 :
Résoudre dans l’équation :
l’équation :
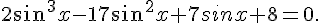
Posons 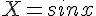
Nous sommes amenés à résoudre :
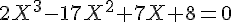
Une racine évidente est X = 1.
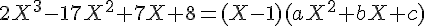
a = 2
-c=8 donc c= -8
c-b=7 donc -8-b=7 ainsi b=-8-7=-15
Donc
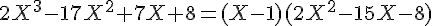
Calculons la valeur du discriminant :
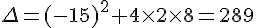
Le discriminant est positif, il existe deux racines réelles distinctes.
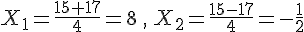
donc
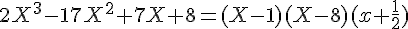
donc nous obtenons :
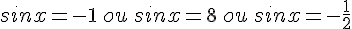
or 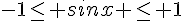
donc soit
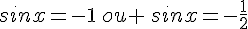
Conclusion :
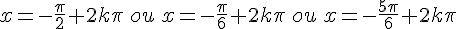
Exercice 7 :
1. On peut déterminer les mesures des angles demandés en utilisant les propriétés des triangles rectangles et de l’angle au centre dans un cercle.
Tout d’abord, le triangle ABC est équilatéral, donc chacun de ses angles mesure 60 degrés.
Dans le triangle BCI, on a un angle droit en I et deux côtés de même longueur (BI = CI car le triangle est isocèle en B), donc c’est un triangle rectangle isocèle, ce qui implique que l’angle 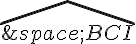 mesure 45 degrés.
mesure 45 degrés.
De même, dans le triangle ACJ, on a un angle droit en J et deux côtés de même longueur (AJ = CJ car le triangle est isocèle en J), donc c’est un triangle rectangle isocèle, ce qui implique que l’angle 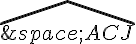 mesure 45 degrés.
mesure 45 degrés.
Pour déterminer l’angle 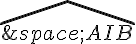 , on peut observer que ce triangle est isocèle en I car AI = IB. On peut également remarquer que ce triangle est inscrit dans le cercle de centre O passant par A, B et I. L’angle \angle AIB mesure donc la moitié de l’angle au centre qui intercepte l’arc AB. Cet arc mesure 60 degrés (car ABC est équilatéral), donc l’angle
, on peut observer que ce triangle est isocèle en I car AI = IB. On peut également remarquer que ce triangle est inscrit dans le cercle de centre O passant par A, B et I. L’angle \angle AIB mesure donc la moitié de l’angle au centre qui intercepte l’arc AB. Cet arc mesure 60 degrés (car ABC est équilatéral), donc l’angle 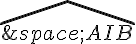 mesure 30 degrés.
mesure 30 degrés.
Enfin, pour déterminer l’angle 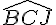 , on peut utiliser la propriété de l’angle inscrit dans un cercle : l’angle
, on peut utiliser la propriété de l’angle inscrit dans un cercle : l’angle 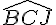 mesure la moitié de l’arc BC du cercle circonscrit au triangle ABC. Comme ABC est équilatéral, l’arc BC mesure 60 degrés, donc l’angle
mesure la moitié de l’arc BC du cercle circonscrit au triangle ABC. Comme ABC est équilatéral, l’arc BC mesure 60 degrés, donc l’angle 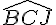 mesure 30 degrés.
mesure 30 degrés.
De même, l’angle 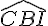 mesure la moitié de l’arc BI du cercle circonscrit au triangle BCI. Cet arc mesure 90 degrés (car le triangle est rectangle en I), donc l’angle
mesure la moitié de l’arc BI du cercle circonscrit au triangle BCI. Cet arc mesure 90 degrés (car le triangle est rectangle en I), donc l’angle 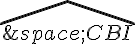 mesure 45 degrés.
mesure 45 degrés.
Ainsi, on a :
-
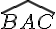 = 60 degrés
= 60 degrés -
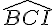 = 45 degrés
= 45 degrés -
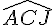 = 45 degrés
= 45 degrés -
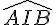 = 30 degrés
= 30 degrés -
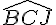 = 30 degrés
= 30 degrés -
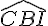 = 45 degrés
= 45 degrés
2. On doit montrer que les points A, I et J sont alignés.
Pour cela, on peut utiliser le fait que dans un triangle rectangle, le milieu de l’hypoténuse est également le centre du cercle circonscrit et donc que la droite passant par le milieu de l’hypoténuse et l’angle droit est un diamètre de ce cercle.
Dans le triangle ACJ, on a un angle droit en J et les côtés AJ et CJ sont de même longueur. Par conséquent, le point milieu M de [AC] est également le centre du cercle circonscrit au triangle ACJ. De plus, la droite (JM) est un diamètre de ce cercle.
Dans le triangle BCI, on a un angle droit en I et les côtés BI et CI sont de même longueur. Par conséquent, le point milieu N de [BC] est également le centre du cercle circonscrit au triangle BCI. De plus, la droite (IN) est un diamètre de ce cercle.
Comme ces deux cercles ont le même diamètre (car les côtés BI et CJ sont de même longueur), les droites (JM) et (IN) se coupent en leur milieu K, qui est également le centre de ces cercles.
Mais ce point K est également le milieu de [AJ] et de [CI]. Par conséquent, les points A, I et J sont alignés sur la droite (AK), qui est la droite passant par les milieux de [AJ] et [CI].
Exercice 8 :
Exercice 9 :
On peut utiliser les propriétés du cercle trigonométrique pour déterminer les mesures principales des angles donnés :
1. Pour l’angle 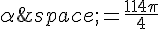 , il y a deux façons de trouver une mesure principale :
, il y a deux façons de trouver une mesure principale :
– On peut diviser l’angle par 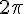 pour obtenir
pour obtenir 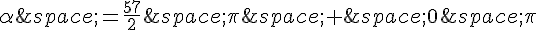 .
.
Comme 0 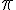 est une mesure principale, on peut donc dire que
est une mesure principale, on peut donc dire que  a pour mesure principale
a pour mesure principale 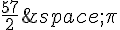 .
.
– On peut soustraire 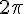 (ou un multiple de
(ou un multiple de 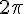 ) de l’angle jusqu’à ce que l’angle obtenu soit entre 0 inclus et 2
) de l’angle jusqu’à ce que l’angle obtenu soit entre 0 inclus et 2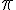 exclus.
exclus.
On a alors 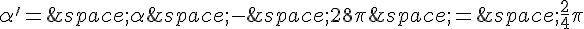 , qui est une mesure principale.
, qui est une mesure principale.
Donc,  a également pour mesure principale
a également pour mesure principale 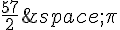 .
.
2. Pour l’angle  , on peut ajouter 2
, on peut ajouter 2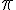 (ou un multiple de 2
(ou un multiple de 2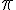 ) à l’angle jusqu’à ce que l’angle obtenu soit entre –
) à l’angle jusqu’à ce que l’angle obtenu soit entre –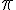 inclus et
inclus et 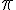 exclus.
exclus.
On a alors 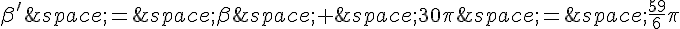 , qui est une mesure principale. Donc,
, qui est une mesure principale. Donc, 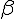 a pour mesure principale
a pour mesure principale 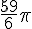 .
.
3. Pour l’angle 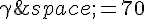 , on peut ajouter un multiple de 360 degrés (ou un multiple de 2
, on peut ajouter un multiple de 360 degrés (ou un multiple de 2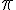 ) à l’angle jusqu’à ce que l’angle obtenu soit entre 0 inclus et 360 degrés exclus (ou entre 0 inclus et 2
) à l’angle jusqu’à ce que l’angle obtenu soit entre 0 inclus et 360 degrés exclus (ou entre 0 inclus et 2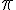 exclus). Comme 70 est déjà une mesure entre 0 et 360 degrés, l’angle
exclus). Comme 70 est déjà une mesure entre 0 et 360 degrés, l’angle 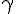 a pour mesure principale 70 degrés (ou
a pour mesure principale 70 degrés (ou  ).
).
Exercice 10 :
ABC est un triangle avec 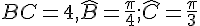 .
.
1. Démontrer que 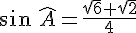 .
.
2. Calculer les valeurs exactes de AB et AC .
Indications :
Utiliser les formules d’Al-Kashi et le théorème de Pythagore généralisé.
Exercice 11 :
Démontrer que la représentation graphique de la fonction définie sur
définie sur  par :
par :
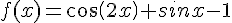
est située entre les droites d’équation y = – 3 et y = 1 .
Tout cela vient du fait que 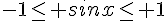 et
et 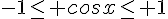 .
.
Il suffit d’additionner chaque membre .
Exercice 12 :
Démontrer que, pour tout réel  :
:
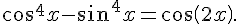
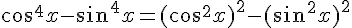
Utilisons l’identité remarquable 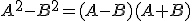
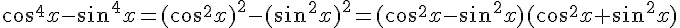
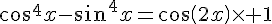 car
car 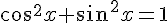 et
et 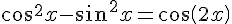
Conclusion : 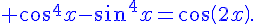
Exercice 13 :
En utilisant les formules d’addition, calculer la valeur exacte de 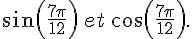
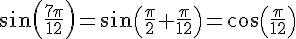
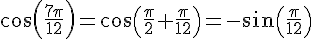
Exercice 14 :
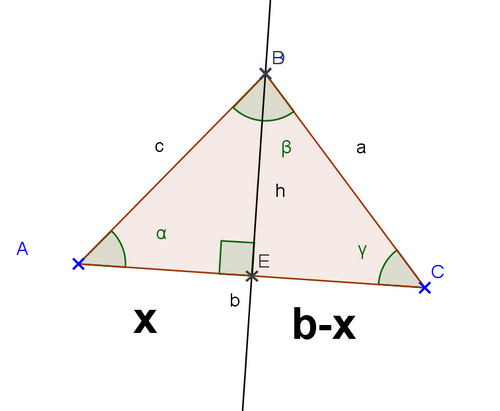
Soit ABC un triangle quelconque.
Dans les triangles AEB et BEC rectangles en E ,
en appliquant le théorème de Pythagore :
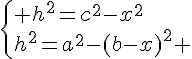
donc par égalité, nous en déduisons que :
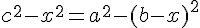
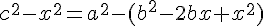

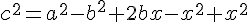
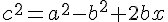 (*)
(*)
Dans le triangle AEB rectangle en E, en utilisant la trigonométrie dans le triangle rectangle :
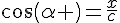
donc
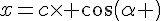
Reprenons l’égalité (*)

Remarque : ce sont les mêmes démonstrations pour les autres formules d’Al-Kashi,
que l’on appelle également formules de Pythagore généralisées.
Exercice 15 :
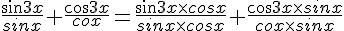
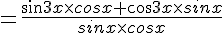
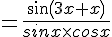
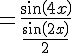
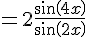
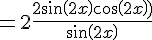

Exercice 16 :
On peut utiliser la formule de l’angle orienté entre deux vecteurs pour calculer la mesure principale de 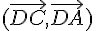 :
:
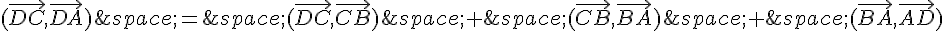
En utilisant les données fournies, on peut écrire :
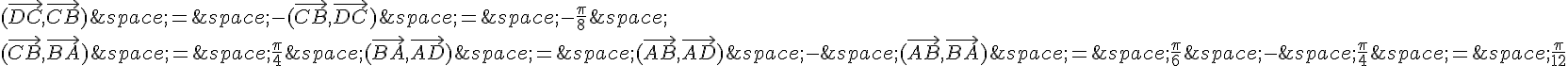
En substituant ces valeurs dans la formule de l’angle orienté, on obtient :
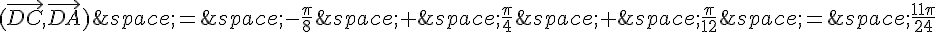
Comme cette mesure n’est pas comprise entre -\pi et \pi, on doit la ramener dans cette intervalle en ajoutant ou soustrayant un multiple de 2\pi. On peut écrire :
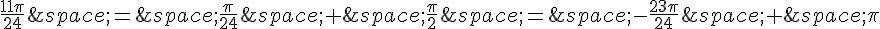
Donc, la mesure principale de 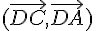 est
est 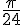 ou
ou 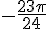 .
.
Exercice 17 :
1. On peut utiliser la loi des sinus pour trouver 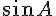 :
:
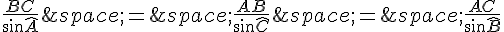
En substituant les valeurs définies, on a :
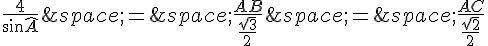
En résolvant pour AB et AC, on obtient :
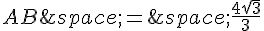 et
et 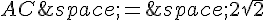
En remplaçant dans la première équation de la loi des sinus, on trouve :

Donc,
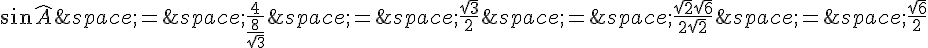
Puisque A appartient à l’intervalle [0, \pi], alors 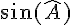 est positif.
est positif.
Ainsi, 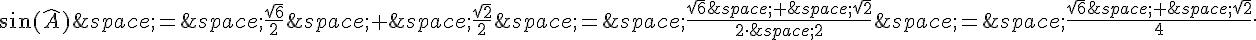
2. On peut utiliser le théorème de Pythagore pour trouver la longueur de AB :
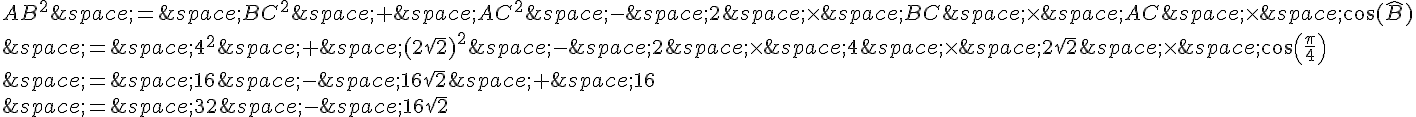
On peut utiliser le même théorème de Pythagore pour trouver la longueur de AC :
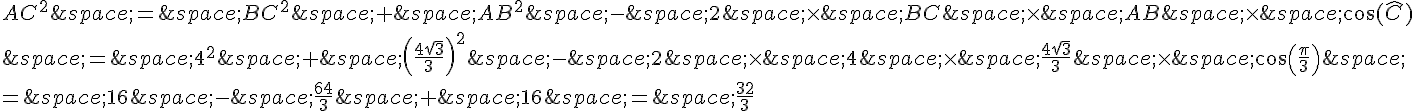
3. L’aire du triangle ABC est donnée par la formule :
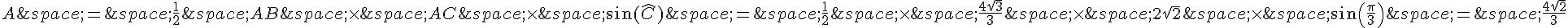
Exercice 18 :
On peut utiliser la formule de l’aire d’un triangle pour trouver la longueur du troisième côté a = BC :
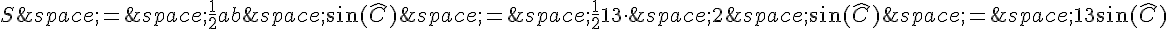
Donc, 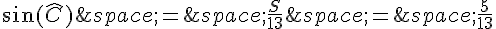 .
.
Comme  est compris entre 0 et 1, alors il existe un unique angle A tel que
est compris entre 0 et 1, alors il existe un unique angle A tel que 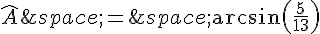 .
.
On peut utiliser la loi des cosinus pour trouver la longueur du troisième côté :
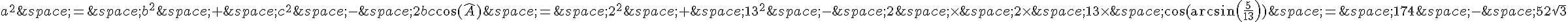
Donc, la seule longueur possible pour le troisième côté est 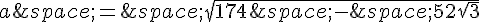 .
.
Exercice 19 :
On peut utiliser la loi des cosinus pour trouver la longueur du troisième côté BC :
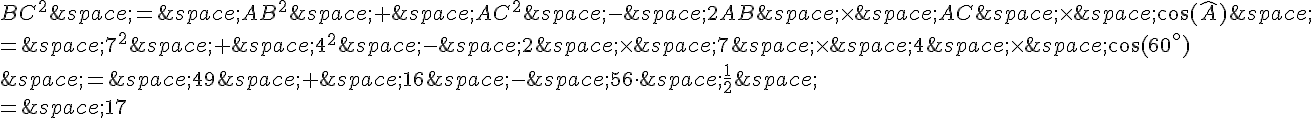
Donc, 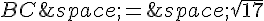 .
.
On peut utiliser la loi des sinus pour trouver 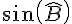 :
:

Exercice 20 :
Soient  et
et 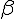 deux angles supplémentaires. Cela signifie que
deux angles supplémentaires. Cela signifie que 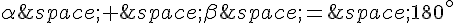 . Alors, on peut écrire :
. Alors, on peut écrire :
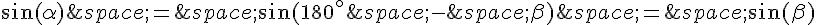
En effet,
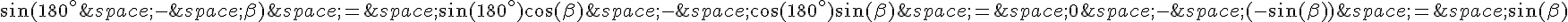
Maintenant, pour démontrer la formule de l’aire du quadrilatère ABCD, on peut diviser le quadrilatère en deux triangles en traçant la diagonale AC. Alors, on peut écrire :
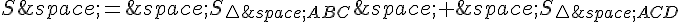
où 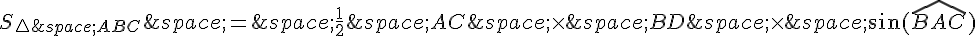 et
et 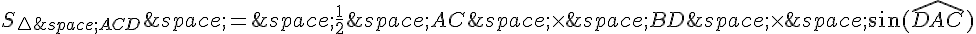 .
.
Donc, 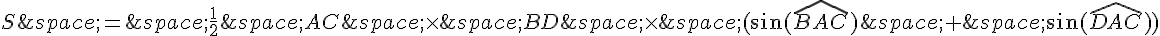 .
.
Mais on sait que les angles BAC et DAC sont supplémentaires, donc on peut utiliser la relation démontrée au début pour écrire :
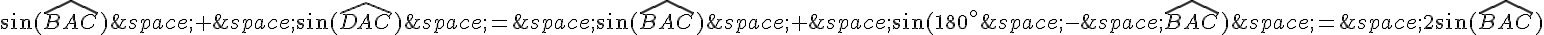
Donc,
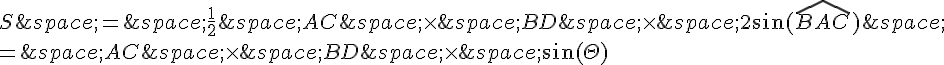
, où  est l’angle formé par les diagonales AC et BD.
est l’angle formé par les diagonales AC et BD.
Exercice 21 :
Le promeneur forme un triangle isocèle avec son point de départ et le point où il a fini de marcher. La première étape de son trajet forme un côté est de ce triangle, la deuxième étape forme un côté nord-est, et la ligne droite qu’il prend pour revenir forme la base de ce triangle.
On peut utiliser le théorème de Pythagore pour trouver la longueur de chaque côté de ce triangle :
côté est : 5 km
côté nord-est : 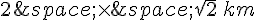
base : 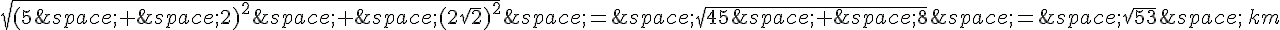
La distance totale parcourue en courant pour rentrer au point de départ est donc de 2 fois la base :
distance parcourue = 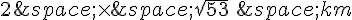
Cette valeur approchée à 0,01 km près est environ 15,46 km.
Exercice 22 :
Dans un triangle ABC, le théorème de Pythagore donne :
– si ABC est rectangle en A alors AB² = AC² + BC²
– si AB² = AC² + BC² alors le triangle ABC est rectangle en A ou B ou C.
Dans le cas où ABC est rectangle en A, on a donc :
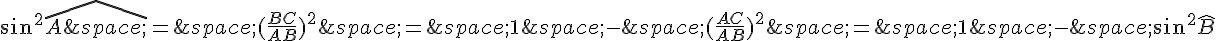
or, dans un triangle, la somme des carrés des sinus des angles est égale à 2 (identité remarquable) :
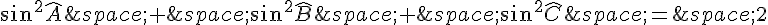
donc :
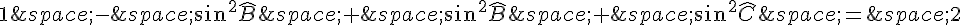
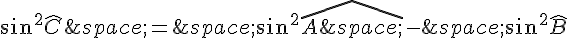
De même, en utilisant le théorème de Pythagore pour les côtés AC et AB, on trouve :
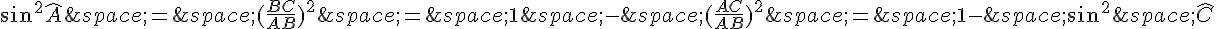
donc :
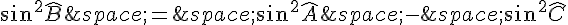
En remplaçant ces expressions dans celle à démontrer :

On a donc bien démontré que si ABC est un triangle rectangle en A, alors  .
.
Réciproquement, supposons que  .
.
On a dans un triangle :
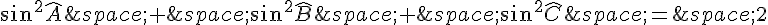
soit :
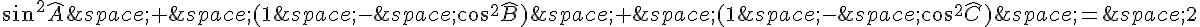
soit :

or, dans un triangle rectangle en A, on a :

donc :
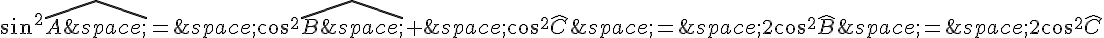
d’où :
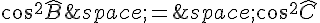
et donc :
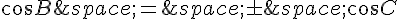
si 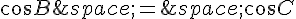 alors l’angle
alors l’angle 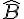 et l’angle
et l’angle 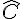 sont égaux ou supplémentaires, donc si
sont égaux ou supplémentaires, donc si 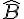 et
et 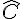 sont différents l’un d’eux est droit, donc ABC est rectangle.
sont différents l’un d’eux est droit, donc ABC est rectangle.
Sinon, on a 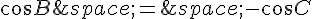 ,
,
alors l’angle 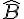 et l’angle
et l’angle 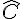 sont supplémentaires, donc l’un d’eux est droit, donc ABC est rectangle.
sont supplémentaires, donc l’un d’eux est droit, donc ABC est rectangle.
Ainsi, si  , alors ABC est un triangle rectangle en A.
, alors ABC est un triangle rectangle en A.
EXERCICE 23 :
1) On a :
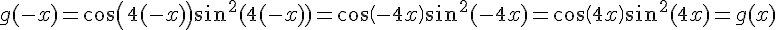
Donc g est une fonction paire, ce qui signifie que son graphe est symétrique par rapport à l’axe des ordonnées.
2) On a :
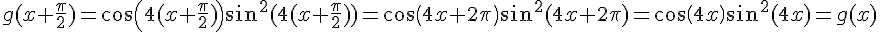
Donc g est une fonction 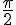 -périodique, c’est-à-dire que son graphe se répète tous les
-périodique, c’est-à-dire que son graphe se répète tous les 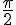 .
.
EXERCICE 24 :
1) On a :
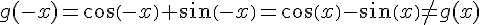
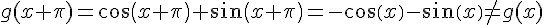
Donc g n’est ni paire ni impaire.
2) On a :
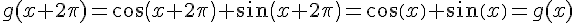
Donc g est une fonction 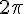 -périodique, c’est-à-dire que son graphe se répète tous les
-périodique, c’est-à-dire que son graphe se répète tous les 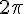 .
.
3) On remarque que :
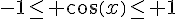
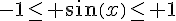
Donc en ajoutant les deux inégalités, on obtient :
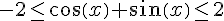
Donc pour tout réel x, 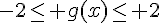 .
.
EXERCICE 25 :
1) On a 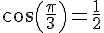 , donc
, donc 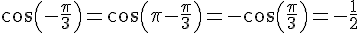 .
.
De plus, 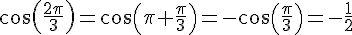 .
.
2) On a 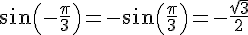 .
.
De plus,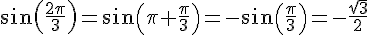 .
.
EXERCICE 26 :
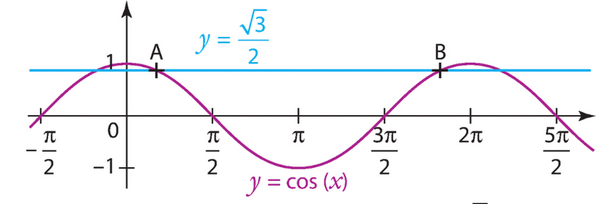
1) On a 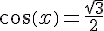 lorsque
lorsque 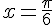 ou
ou 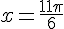 (car cos est positif sur
(car cos est positif sur ![[0,\pi]](https://mathovore.fr/latex-images/a79560c6f70853be01bb23f7539e168c.png) et
et 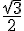 est l’une des valeurs que peut prendre cos à ces deux angles).
est l’une des valeurs que peut prendre cos à ces deux angles).
2) On a 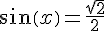 lorsque
lorsque 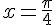 ou
ou 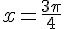 (car sin est positif sur
(car sin est positif sur ![[\frac{\pi}{2},\frac{3\pi}{2}]](https://mathovore.fr/latex-images/2f4a052e2861b2f603c8798a6e60f35d.png) et
et 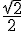 est l’une des valeurs que peut prendre sin à ces deux angles).
est l’une des valeurs que peut prendre sin à ces deux angles).
EXERCICE 27 :
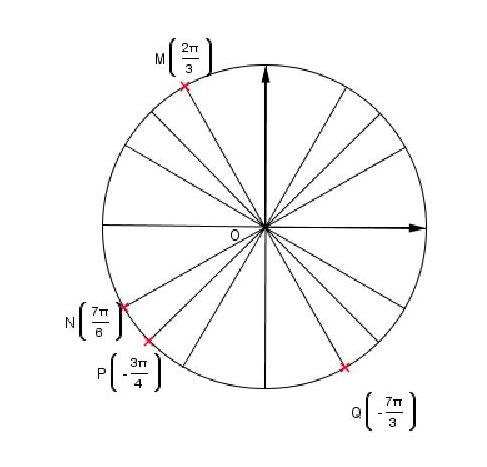
1. Les abscisses des points A et B sont respectivement  et
et 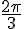 .
.
2. Les solutions sur  de l’équation
de l’équation 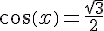 sont
sont 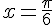 et
et 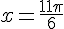 .
.
3. Les solutions sur  de l’inéquation
de l’inéquation 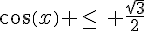 sont
sont ![x\in[0,\frac{\pi}{6}]\cup[\frac{5\pi}{6},\pi]\cup[\frac{7\pi}{6},2\pi]](https://mathovore.fr/latex-images/bf73f34a2dcd23044a4ff7f64e277fdf.png) .
.
EXERCICE 28 :
a) On a 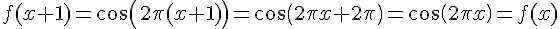 pour tout réel x, donc f est bien T-périodique avec T=1.
pour tout réel x, donc f est bien T-périodique avec T=1.
b) On a 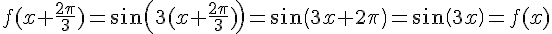 pour tout réel x, donc f est bien T-périodique avec
pour tout réel x, donc f est bien T-périodique avec 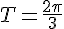 .
.
c) On a 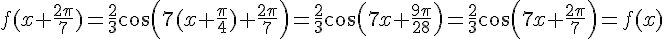 pour tout réel x, donc f est bien T-périodique avec
pour tout réel x, donc f est bien T-périodique avec 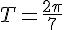 .
.
d) On a 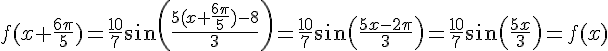 pour tout réel x, donc f est bien T-périodique avec
pour tout réel x, donc f est bien T-périodique avec 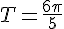 .
.
EXERCICE 29 :
1.a) On a 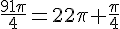 , donc x=-\frac{\pi}{4}.
, donc x=-\frac{\pi}{4}.
b) 
et 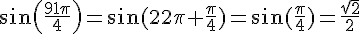 .
.
2.a) 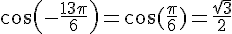 .
.
b)  .
.
3.a) 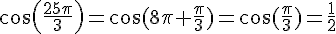 , donc
, donc 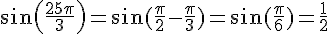 .
.
b) 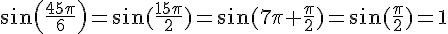 , donc
, donc 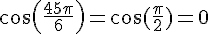 .
.
EXERCICE 30 :
1.a) Comme f est définie sur ![]-\pi ; \pi]](https://mathovore.fr/latex-images/b22ed071b4720021977c7b8ebbd55d3b.png) , on a
, on a 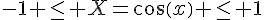 .
.
b) En résolvant l’équation 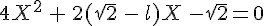 , on trouve
, on trouve 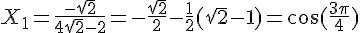 et
et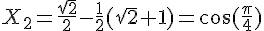 .
.
c) Les solutions sur [-1,1] de l’équation 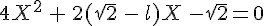 sont
sont 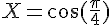 et
et 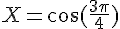 .
.
d) En utilisant le fait que cos(x)=X, on en déduit les solutions de l’équation f(x)=0 sur ![]-\pi ; \pi]](https://mathovore.fr/latex-images/b22ed071b4720021977c7b8ebbd55d3b.png) :
: 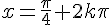 et
et  pour
pour 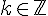 .
.
2. Les solutions sur [-1,1] de l’inéquation 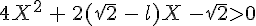 sont
sont
![X \in ]-\infty,\frac{-\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}[\cup]\frac{\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2},\frac{-\sqrt{2}}{4}[\cup]\frac{\sqrt{2}}{4},\frac{\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}[\cup]\frac{-\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2},+\infty[](https://mathovore.fr/latex-images/ec620f270b1d0b66590ac8b21ee79c97.png) .
.
En utilisant le fait que 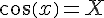 , on en déduit les solutions de l’inéquation
, on en déduit les solutions de l’inéquation 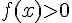 sur
sur ![]-\pi ; \pi]](https://mathovore.fr/latex-images/b22ed071b4720021977c7b8ebbd55d3b.png) :
:
![x \in ]\arccos(\frac{-\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}),\arccos(\frac{\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2})[\cup]\arccos(\frac{\sqrt{2}}{4}),\arccos(\frac{\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2})[](https://mathovore.fr/latex-images/215084a0ca72d66beb7cc5260d6d820c.png) .
.
EXERCICE 31 :
1. Le disque tourne 33 tours et 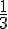 de tour par minute, donc il tourne pendant
de tour par minute, donc il tourne pendant 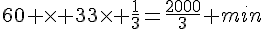 .
.
Chaque chanson a donc une durée de 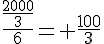 min.
min.
Le saphir se trouvera donc sur le demi-axe négatif à la fin de chaque chanson, c’est-à-dire après une durée de 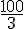 min.
min.
2. Le disque tourne 16 tours et 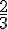 de tour par minute, donc il tourne pendant
de tour par minute, donc il tourne pendant 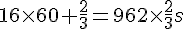 .
.
Chaque chanson a donc une durée de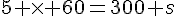 .
.
a) Après 3 min=180 s, le saphir aura parcouru un angle de 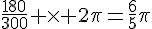 .
.
Il se trouvera donc sur le demi-axe positif.
b) Après 4 min=240 s, le saphir aura parcouru un angle de  .
.
Il se trouvera donc sur le demi-axe négatif.
c) A la fin de la première chanson, le saphir aura parcouru un angle de 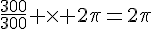 .
.
Il reviendra donc à la position de départ sur le demi-axe positif.
d) A la fin de la deuxième chanson, le saphir aura parcouru un angle de 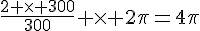 . Il se trouvera donc sur le demi-axe négatif.
. Il se trouvera donc sur le demi-axe négatif.
EXERCICE 32 :
1. La fonction cos est paire et 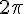 -périodique, donc la fonction f est également paire et
-périodique, donc la fonction f est également paire et 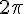 -périodique. Graphiquement, cela signifie que la courbe représentative de f est symétrique par rapport à l’axe des ordonnées et qu’elle se répète identiquement tous les
-périodique. Graphiquement, cela signifie que la courbe représentative de f est symétrique par rapport à l’axe des ordonnées et qu’elle se répète identiquement tous les 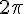 .
.
2. Comme f est 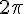 -périodique, il suffit d’étudier la fonction sur un intervalle de longueur
-périodique, il suffit d’étudier la fonction sur un intervalle de longueur 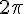 .
.
Le plus petit intervalle possible est donc ![[-\pi;\pi]](https://mathovore.fr/latex-images/32256bda626c2d0b438cdcfb65d8f9fd.png) .
.
3. a) La fonction f’ est définie et dérivable sur tout  , sauf en les points où
, sauf en les points où 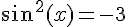 (ce qui n’a pas de sens).
(ce qui n’a pas de sens).
Sur les autres points, on a
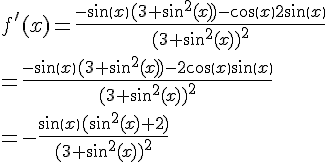 .
.
Comme 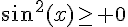 , on a
, on a 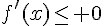 si
si  et
et 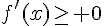 si
si 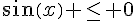 .
.
b) Les extrema locaux de f sont les points où 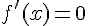 ou
ou  n’est pas dérivable.
n’est pas dérivable.
Les points où f est pas dérivable sont les points où 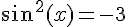 , qui n’existent pas. Donc les seuls points où f'(x)=0 sont les points où sin(x)=0, c’est-à-dire les multiples entiers de \pi.
, qui n’existent pas. Donc les seuls points où f'(x)=0 sont les points où sin(x)=0, c’est-à-dire les multiples entiers de \pi.
c) Sur l’intervalle ![[-\pi;\pi]](https://mathovore.fr/latex-images/32256bda626c2d0b438cdcfb65d8f9fd.png) , f est décroissante sur
, f est décroissante sur ![[-\pi;0]](https://mathovore.fr/latex-images/36ea01d41f69f85844b1731db98cfadf.png) et croissante sur
et croissante sur ![[0;\pi]](https://mathovore.fr/latex-images/877f17aad9bc954cb768bda41864129d.png) .
.
Le minimum de f est donc atteint en  , où
, où  , et le maximum est atteint en x=0, où
, et le maximum est atteint en x=0, où 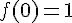 .
.
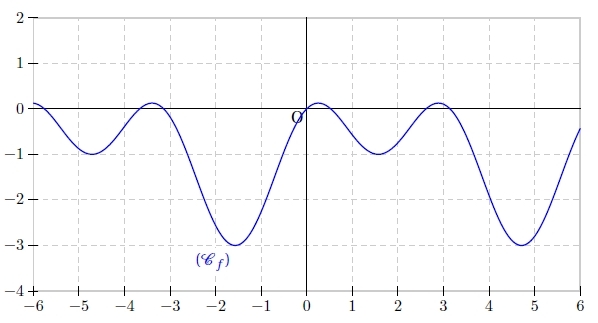
Pour tracer la courbe de f sur ![[-\pi;3\pi]](https://mathovore.fr/latex-images/7ae743612ec5ff2f72edbca1992392b7.png) , on peut se baser sur la périodicité de f : f est
, on peut se baser sur la périodicité de f : f est 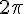 -périodique donc il suffit de tracer la courbe sur un intervalle de longueur
-périodique donc il suffit de tracer la courbe sur un intervalle de longueur 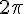 et de la répéter ensuite identiquement sur chaque intervalle de même longueur.
et de la répéter ensuite identiquement sur chaque intervalle de même longueur.
On peut donc tracer la courbe de f sur ![[0,2\pi]](https://mathovore.fr/latex-images/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) et ensuite représenter cette courbe sur chaque intervalle
et ensuite représenter cette courbe sur chaque intervalle![[2k\pi ; (2k+2)\pi]](https://mathovore.fr/latex-images/b82586a51c2268fc4896357f5b961284.png) en la décalant horizontalement de
en la décalant horizontalement de 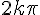 .
.
EXERCICE 33 :
1. La fonction cos est paire, donc la fonction f est également paire et 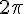 -périodique.
-périodique.
Graphiquement, cela signifie que la courbe représentative de f est symétrique par rapport à l’axe des ordonnées et qu’elle se répète identiquement tous les 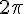 .
.
2. La fonction f’ est définie et dérivable sur tout  .
.
Sur cet intervalle, f’ est positive si 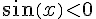 , c’est-à-dire si
, c’est-à-dire si ![x\in]\pi,2\pi[](https://mathovore.fr/latex-images/59f3b176bd380da41d72dfe9ef897cae.png) , et négative si
, et négative si 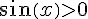 , c’est-à-dire si
, c’est-à-dire si ![x\in ]0,\pi [](https://mathovore.fr/latex-images/38bd77af09a5bdc9bd1346753a043575.png) .
.
Donc f est croissante sur ![[0,\pi]](https://mathovore.fr/latex-images/a79560c6f70853be01bb23f7539e168c.png) et décroissante sur
et décroissante sur ![[\pi,2\pi]](https://mathovore.fr/latex-images/47b7f230fdecba2be3593db374912e75.png) .
.
3. Sur l’intervalle ![[0,2\pi]](https://mathovore.fr/latex-images/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) , f est décroissante sur
, f est décroissante sur ![[0,\pi]](https://mathovore.fr/latex-images/a79560c6f70853be01bb23f7539e168c.png) et croissante sur
et croissante sur ![[\pi,2\pi]](https://mathovore.fr/latex-images/47b7f230fdecba2be3593db374912e75.png) . Le minimum de f est donc atteint en
. Le minimum de f est donc atteint en  , où
, où  , et le maximum est atteint en
, et le maximum est atteint en 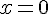 et en
et en 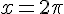 , où
, où 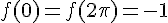 .
.
Ensuite, on peut dresser le tableau de variations de f sur l’intervalle ![[-\pi;\frac{3}{\pi}]](https://mathovore.fr/latex-images/b84d8b4ee1d631c04d3c4a83bf60defc.png) en répétant le tableau sur chaque intervalle
en répétant le tableau sur chaque intervalle ![[2k\pi ; (2k+2)\pi]](https://mathovore.fr/latex-images/b82586a51c2268fc4896357f5b961284.png) et en décalant horizontalement en cela pour chaque table.
et en décalant horizontalement en cela pour chaque table.
EXERCICE 34 :
1. Puisque 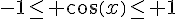 pour tout x, on a
pour tout x, on a 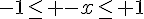 , donc les solutions de l’équation
, donc les solutions de l’équation 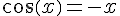 sont dans l’intervalle [-1,1].
sont dans l’intervalle [-1,1].
2. La fonction f est définie et dérivable sur [-1,1], donc elle est continue sur cet intervalle.
Puisque 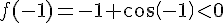 et
et 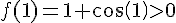 , la courbe de f rencontre l’axe des abscisses au moins une fois dans l’intervalle
, la courbe de f rencontre l’axe des abscisses au moins une fois dans l’intervalle ![[-1,1]](https://mathovore.fr/latex-images/d060b17b29e0dae91a1cac23ea62281a.png) .
.
On peut conjecturer que l’équation cos(x)=-x admet une unique solution dans cet intervalle, qui correspond à l’abscisse de l’intersection de la courbe de f avec l’axe des abscisses.
b) f'(x)=-sin(x)+1, donc f'(x) est positive si sin(x)<1, c’est-à-dire si ![x\in ]-\frac{\pi}{2},\frac{\pi}{2}[](https://mathovore.fr/latex-images/59529c37f3400327c51220dd8f885ecd.png) , et négative si
, et négative si 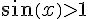 , c’est-à-dire si
, c’est-à-dire si ![x\in ]\frac{\pi}{2},\frac{3\pi}{2}[](https://mathovore.fr/latex-images/10dfd234b33dc4cd03a11f360685653e.png) .
.
Donc f est croissante sur [-1,0] et décroissante sur [0,1].
c) En partant du tableau de variations de 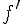 , on peut en déduire le tableau de variations de f sur [-1,1]. Puisque la fonction est croissante sur [-1,0] et décroissante sur [0,1], elle admet un unique zéro sur l’intervalle [0,1], correspondant donc à l’unique solution de l’équation
, on peut en déduire le tableau de variations de f sur [-1,1]. Puisque la fonction est croissante sur [-1,0] et décroissante sur [0,1], elle admet un unique zéro sur l’intervalle [0,1], correspondant donc à l’unique solution de l’équation 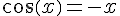 dans l’intervalle [-1,1].
dans l’intervalle [-1,1].
d) A l’aide d’une calculatrice, on obtient une valeur approchée de la solution de l’équation 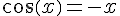 dans l’intervalle [-1,1] :
dans l’intervalle [-1,1] : 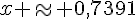 .
.
EXERCICE 35 :
1. La lentille parcourt un angle de 360° en 5 secondes, donc elle parcourt un angle de 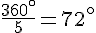 en 1 seconde.
en 1 seconde.
2. L’aire balayée par la lentille en 1 seconde est proportionnelle à l’angle parcouru en 1 seconde, donc elle vaut  .
.
EXERCICE 36 :
1. La fonction cos est paire, donc pour tout réel x, on a 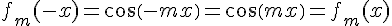 . La fonction
. La fonction 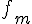 est donc paire.
est donc paire.
Graphiquement, cela signifie que la courbe représentative de 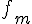 est symétrique par rapport à l’axe des ordonnées.
est symétrique par rapport à l’axe des ordonnées.
2. Pour tout réel x, on a 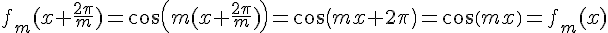 .
.
La fonction 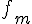 est donc périodique de période
est donc périodique de période  .
.
3. Puisque cos(x) est périodique de période 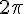 , la fonction
, la fonction 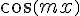 est périodique de période
est périodique de période  .
.
On peut donc se limiter à étudier 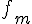 sur l’intervalle
sur l’intervalle![[0,\frac{2\pi}{m}]](https://mathovore.fr/latex-images/3324ae346d239c70145ff6a54d8d7f19.png) , c’est-à-dire sur l’intervalle
, c’est-à-dire sur l’intervalle ![[0,\frac{\pi}{m}]](https://mathovore.fr/latex-images/a4e69f8a9ac5022f577c67f7a52625ef.png) si on se restreint aux valeurs positives de x.
si on se restreint aux valeurs positives de x.
4. a) La fonction 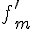 est définie et dérivable sur tout
est définie et dérivable sur tout  , donc elle est continue sur tout
, donc elle est continue sur tout  .
.
Puisque le sin est positif sur ![[0,\frac{\pi}{m}]](https://mathovore.fr/latex-images/a4e69f8a9ac5022f577c67f7a52625ef.png) , on a
, on a 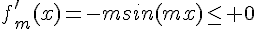 sur cet intervalle.
sur cet intervalle.
b) D’après le tableau de variations de 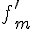 , la fonction
, la fonction 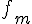 est décroissante sur
est décroissante sur ![[0,\frac{\pi}{m}]](https://mathovore.fr/latex-images/a4e69f8a9ac5022f577c67f7a52625ef.png) .
.
c) Si 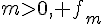 admet un maximum en 0 et une valeur minimale en
admet un maximum en 0 et une valeur minimale en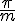 , qui sont respectivement
, qui sont respectivement 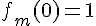 et
et 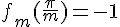 .
.
Par ailleurs, si on considère la périodicité de 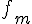 de période
de période  , on peut recopier le tableau de variation sur l’intervalle
, on peut recopier le tableau de variation sur l’intervalle ![[0,\frac{\pi}{m}]](https://mathovore.fr/latex-images/a4e69f8a9ac5022f577c67f7a52625ef.png) sur chaque intervalle de la forme
sur chaque intervalle de la forme ![[\frac{2k\pi}{m}, \frac{(2k+1)\pi}{m}]](https://mathovore.fr/latex-images/45a239612f3c4f72182b797794f99f38.png) , en le décalant horizontalement de
, en le décalant horizontalement de 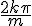 .
.
EXERCICE 37 :
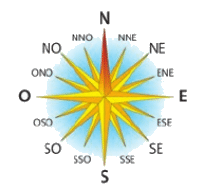
1. Le sens « O » se situe à gauche de l’axe des ordonnées.
Comme l’axe des abscisses correspond au sens « E » et que le sens « S » est dirigé vers le bas, le sens « O » est dirigé vers la gauche et en bas.
Cela correspond donc à un réel négatif qui est plus grand que 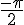 .
.
Par exemple, on peut prendre 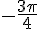 .
.
2. Le sens « S » est dirigé vers le bas de l’axe des ordonnées. Comme le sens « N » correspond à 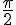 , cela correspond donc à un réel négatif.
, cela correspond donc à un réel négatif.
Comme le sens « S » est à mi-chemin entre le sens « E » et le sens « O », cela correspond donc à un réel qui est le milieu entre 0 et  .
.
On a donc 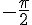 .
.
3. Le sens « NE » fait un angle de  avec l’axe des abscisses. Cela correspond donc au réel
avec l’axe des abscisses. Cela correspond donc au réel  .
.
4. a) Le sens « NNE » fait un angle de 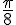 avec l’axe des abscisses. Cela correspond donc au réel
avec l’axe des abscisses. Cela correspond donc au réel 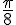 .
.
b) Par symétrie, le sens « SSE » correspond à un angle de 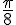 avec l’axe des abscisses, donc cela correspond au réel –
avec l’axe des abscisses, donc cela correspond au réel –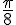 .
.
c) Par symétrie, le sens « NNO » correspond à un angle de  avec l’axe des abscisses mais du côté gauche de l’axe des ordonnées (puisque c’est le symétrique du sens « NE » par rapport à l’axe des ordonnées).
avec l’axe des abscisses mais du côté gauche de l’axe des ordonnées (puisque c’est le symétrique du sens « NE » par rapport à l’axe des ordonnées).
Cela correspond donc à l’opposé du réel  , c’est-à-dire
, c’est-à-dire 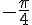 .
.
EXERCICE 38 :

EXERCICE 39 :
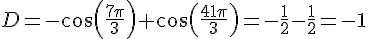
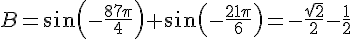
EXERCICE 40 :
Désolé, il n’y a pas de données à partir desquelles résoudre un exercice.
EXERCICE 41 :
1. En utilisant les coordonnées des points M et N, on obtient un système d’équations à deux inconnues a et b :
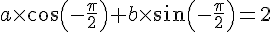
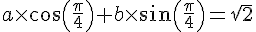
En résolvant ce système, on trouve 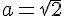 et
et 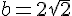 .
.
2. En utilisant les valeurs de a et b obtenues, on peut écrire :
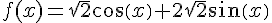
3. Pour montrer que f est 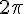 -périodique, on peut calculer
-périodique, on peut calculer 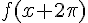 et vérifier qu’on obtient la même expression que
et vérifier qu’on obtient la même expression que 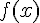 .
.
En effectuant les calculs, on obtient :
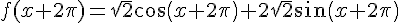
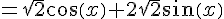
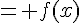
Ceci signifie que si on trace la courbe représentative de f sur un intervalle ![[a, a+2\pi]](https://mathovore.fr/latex-images/39403eabdbd0f52d719433dee7779c81.png) , on pourra la décaler de 2\pi pour obtenir la courbe sur l’intervalle
, on pourra la décaler de 2\pi pour obtenir la courbe sur l’intervalle ![[a+2\pi, a+4\pi]](https://mathovore.fr/latex-images/5c9a52d93c15f9f5fac4dcd18dd503a7.png) , et ainsi de suite.
, et ainsi de suite.
4. Pour déterminer si f est paire ou impaire, il faut vérifier si 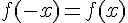 (cas d’une fonction paire) ou
(cas d’une fonction paire) ou 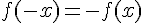 (cas d’une fonction impaire).
(cas d’une fonction impaire).
En remplaçant x par -x dans l’expression de f, on obtient :
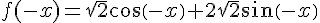
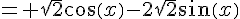
On constate que 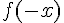 est différent de
est différent de 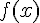 et de
et de 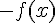 , donc f n’est ni paire ni impaire.
, donc f n’est ni paire ni impaire.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «trigonométrie : corrigé des exercices de maths en 1ère en PDF.» au format PDF.
Ressources de première
Cours de première
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.