Barycentre : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 19 septembre 2025
Exercice 1 :
Soit $G$ le centre de gravité de 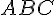 .
.
On sait que les barycentres sont des combinaisons linéaires des sommets, donc il existe des nombres 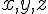 tels que :
tels que :
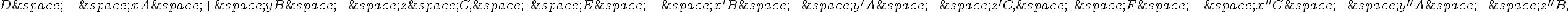
où 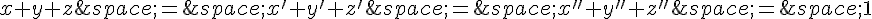 .
.
On sait que le barycentre de $n$ points de masses respectives 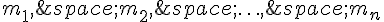 et de barycentres $G_1, G_2,
et de barycentres $G_1, G_2, 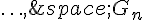 est le point de barycentre
est le point de barycentre 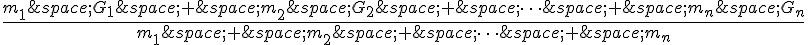 .
.
Ainsi, le barycentre de $(A,1)(B,2)(C,3)$ est 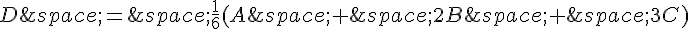 , donc le barycentre de
, donc le barycentre de 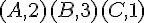 est :
est :

De même, on trouve :
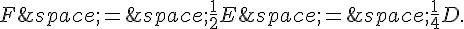
Ainsi, les masses des points $D$, $E$ et $F$ sont respectivement $6$, $2$ et $4$.
Le centre de gravité d’un triangle est le barycentre de ses sommets avec des masses égales. Donc :
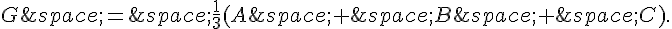
Le centre de gravité de $DEF$ est donc le point de barycentre :

Mais on peut exprimer $G$ avec les mêmes coefficients : 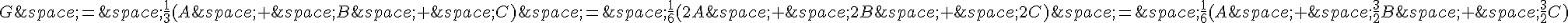 .
.
Ainsi, M est le barycentre de A, B et C avec des masses respectives 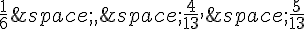 , donc il s’agit bien du centre de gravité de ABC.
, donc il s’agit bien du centre de gravité de ABC.
Exercice 2 :
a) On a 
et 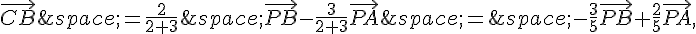 où $P$ est le barycentre de
où $P$ est le barycentre de  .
.
De même, on peut écrire 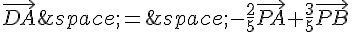 et
et 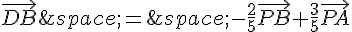 .
.
On cherche les points M tels que 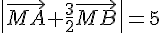 .
.
En développant cette expression, on obtient l’équation suivante :
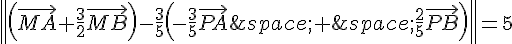 .
.
En d’autres termes, on cherche les points M situés sur la droite passant par  et parallèle à
et parallèle à  (car
(car  est perpendiculaire à la droite passant par M et
est perpendiculaire à la droite passant par M et  ), et tels que
), et tels que  .
.
L’ensemble des points M vérifiant cette équation est donc un cercle de centre 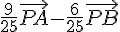 et de rayon 1.
et de rayon 1.
En procédant de même pour la seconde question, on obtient que l’ensemble des points vérifiant l’équation  est un cercle centré en
est un cercle centré en 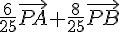 et de rayon
et de rayon 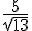 .
.
En effet, on développe l’expression  pour trouver :
pour trouver :
 ce qui montre que la droite passant par A et B est perpendiculaire à la droite passant par M et
ce qui montre que la droite passant par A et B est perpendiculaire à la droite passant par M et 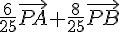 .
.
On a donc que l’ensemble des points solution est un cercle centré sur la droite passant par $A$ et $B$ et de rayon 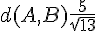 .
.
Exercice 3 :
a) Pour que 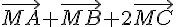 soit colinéaire à
soit colinéaire à 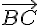 , il faut que les vecteurs
, il faut que les vecteurs 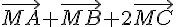 et
et 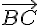 soient parallèles, c’est-à-dire que leur produit vectoriel soit nul (car le produit vectoriel de deux vecteurs non nuls est nul si et seulement s’ils sont parallèles).
soient parallèles, c’est-à-dire que leur produit vectoriel soit nul (car le produit vectoriel de deux vecteurs non nuls est nul si et seulement s’ils sont parallèles).
Donc, on a l’équation suivante :

En développant le produit vectoriel et en utilisant les propriétés du produit vectoriel, on obtient :
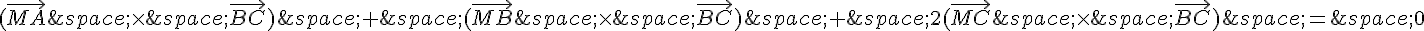 .
.
Donc, pour que 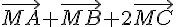 soit colinéaire à \vec{BC}, il faut et il suffit que les vecteurs
soit colinéaire à \vec{BC}, il faut et il suffit que les vecteurs  et
et 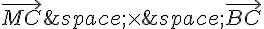 soient tous nuls.
soient tous nuls.
b) Pour que 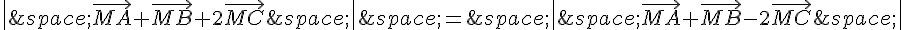
Il faut que le carré de la norme de  soit égal au carré de la norme de
soit égal au carré de la norme de
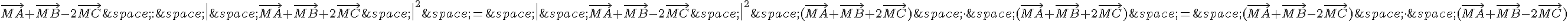 En développant le produit scalaire et en utilisant les propriétés du produit scalaire, on obtient :
En développant le produit scalaire et en utilisant les propriétés du produit scalaire, on obtient : 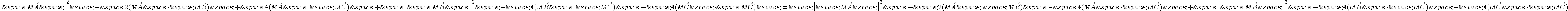
Les termes de même nature s’annulent :
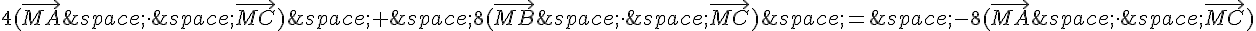
Donc, pour que 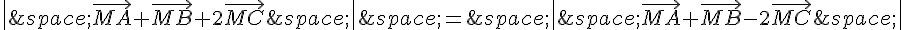 , il faut et il suffit que
, il faut et il suffit que 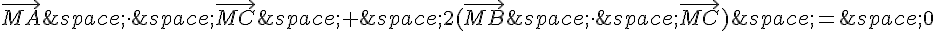 .
.
Exercice 4 :
Pour montrer que les points I, J et K sont alignés, il suffit de montrer que ces trois points sont colinéaires, c’est-à-dire que les vecteurs 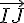 et
et 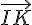 sont parallèles (le vecteur
sont parallèles (le vecteur 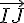 est proportionnel à
est proportionnel à 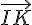 ).
).
Le vecteur 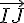 peut s’exprimer en fonction des vecteurs
peut s’exprimer en fonction des vecteurs 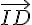 et
et 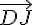 :
: 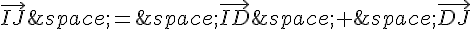
Le vecteur 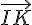 peut s’exprimer en fonction des vecteurs
peut s’exprimer en fonction des vecteurs  et
et 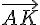 :
: 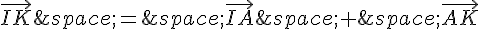
On connaît l’expression des vecteurs 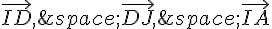 et
et 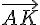 en fonction des vecteurs
en fonction des vecteurs 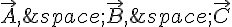 et
et 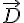 .
.
En développant ces expressions, on obtient :
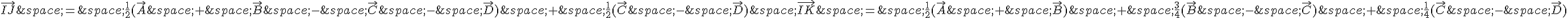
On peut remarquer que les termes  apparaissent dans les expressions de
apparaissent dans les expressions de 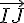 et
et 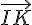 .
.
On peut factoriser ces termes pour simplifier les expressions : 
Maintenant, on peut comparer les expressions de 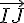 et
et 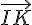 .
.
On remarque que les coefficients devant les vecteurs 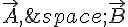 et
et 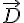 sont les mêmes dans les deux expressions.
sont les mêmes dans les deux expressions.
Donc, les vecteurs 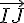 et
et 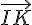 sont parallèles et les points I, J et K sont alignés.
sont parallèles et les points I, J et K sont alignés.
Exercice 5 :
a) Pour montrer que les droites (AC), (BD) et (GH) sont concourantes, il suffit de montrer que les points A, C et G (ou les points B, D et H) sont alignés.
Le point G est le barycentre du système de points pondérés {(A,2);(B,1)}, donc les coordonnées de G peuvent s’exprimer en fonction des coordonnées de A et B :
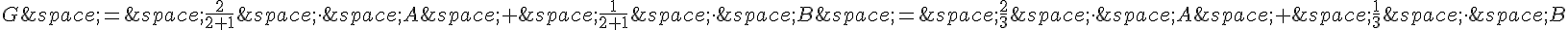
De même, le point H est le barycentre du système de points pondérés {(C,2);(D,1)}, donc les coordonnées de H peuvent s’exprimer en fonction des coordonnées de C et D :
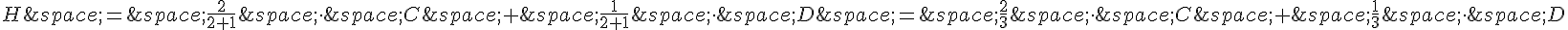
Si les points A, C et G sont alignés, alors les coordonnées de G peuvent également s’exprimer en fonction des coordonnées de A et C :
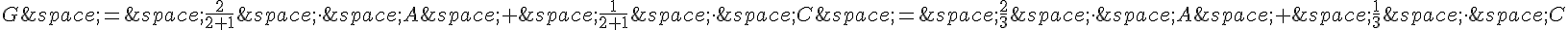
Donc, on a les égalités suivantes :
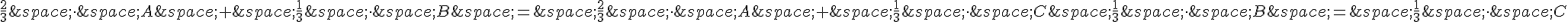
Cela signifie que les coordonnées de B et C sont égales. Donc, les points B et C sont confondus et les droites (AC), (BD) et (GH) sont concourantes.
b) Soit E le barycentre du système de points pondérés {(G,3);(D,1)}. Pour montrer que E est le milieu de [AO], il suffit de montrer que les coordonnées de E sont la moitié des coordonnées de O.
Les coordonnées de G sont données par 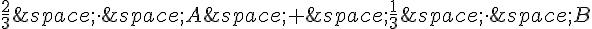 et les coordonnées de D sont simplement les coordonnées de D (puisque son coefficient de pondération est 1).
et les coordonnées de D sont simplement les coordonnées de D (puisque son coefficient de pondération est 1).
Les coordonnées de E peuvent donc être calculées comme suit :
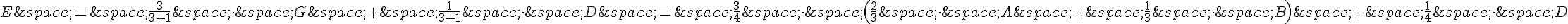
En multipliant et en simplifiant les termes, on obtient :
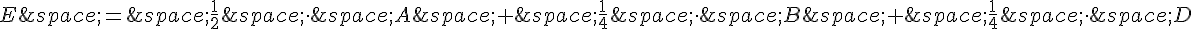
Les coordonnées du centre O du parallélogramme ABCD sont la moyenne des coordonnées de A, B, C et D, c’est-à-dire :
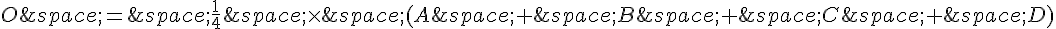
Comparons les coordonnées de E et O :

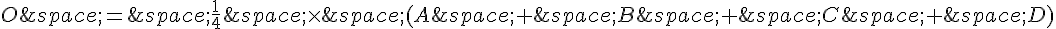
Les coordonnées de E sont la moitié des coordonnées de O. Donc, E est le milieu de [AO].
Exercice 6 :
1. Pour construire le barycentre des points {(A,1);(B,2)} sachant que AB = 6 cm, nous utilisons la formule du barycentre :
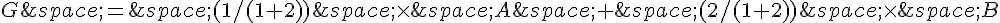
Nous prenons un compas, plaçons sa pointe en A et ouvrons le compas à une longueur de 2 cm (pondération correspondant à B).
Nous traçons un arc de cercle depuis B jusqu’à l’intersection de l’arc de cercle précédent avec le segment AB. Nous notons ce point d’intersection G.
2. Pour construire le barycentre des points {(A,3);(B,-3)} sachant que AB = 8 cm, nous utilisons la même formule du barycentre :
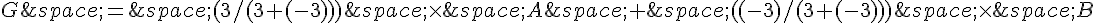
Nous prenons un compas, plaçons sa pointe en A et ouvrons le compas à une longueur de 3 cm (pondération correspondant à A). Nous traçons un arc de cercle depuis B jusqu’à l’intersection de l’arc de cercle précédent avec le segment AB. Nous notons ce point d’intersection G.
3. Pour construire le barycentre des points {(A,1);(B,-2)} sachant que AB = 4 cm, nous utilisons encore la formule du barycentre :
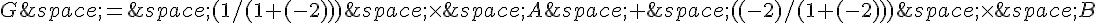
Nous prenons un compas, plaçons sa pointe en B et ouvrons le compas à une longueur de 2 cm (pondération correspondant à B). Nous traçons un arc de cercle depuis A jusqu’à l’intersection de l’arc de cercle précédent avec le segment AB. Nous notons ce point d’intersection G.
4. Pour construire le barycentre des points {(M,-3);(N,-2)} sachant que MN = 10 cm, nous utilisons toujours la formule du barycentre :

Nous prenons un compas, plaçons sa pointe en N et ouvrons le compas à une longueur de 2 cm (pondération correspondant à N). Nous traçons un arc de cercle depuis M jusqu’à l’intersection de l’arc de cercle précédent avec le segment MN. Nous notons ce point d’intersection G.
Exercice 7 :
1. Décrire l’ensemble des points M du plan tels que 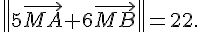
Considérons I barycentre des points (A,5) et (B,6)
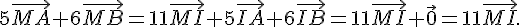
donc l’ensemble correspond au cercle de centre I et de rayon 2 .
2. Décrire l’ensemble des points M du plan tels que 
Considérons I barycentre des points (A,-5) et (B,8)
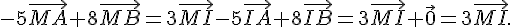
donc l’ensemble correspond au cercle de centre I et de rayon 4 .
3. Décrire l’ensemble des points M du plan tels que 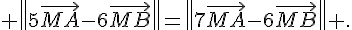
Considérons I barycentre des points (A,5) et (B,-6) et J barycentre des points (A,7) et (B;-6)
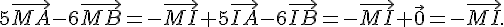
De même : 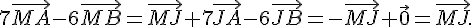
donc nous recherchons les points M tels que MI=MJ, l’ensemble est donc la médiatrice du segment [IJ] .
Exercice 8 :
Soit R un repère orthonormé du plan .
1. Effectuer la construction
2. On note 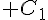 l’ensemble des points M du plan tels que
l’ensemble des points M du plan tels que 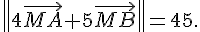 .
.
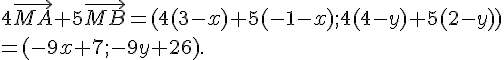 .
.
![\|4\vec{MA}+5\vec{MB}\|=\sqrt{(-9x+7)^2+(-9y+26)^2}\=\sqrt{81[(x-\frac{7}{9})^2+(y-\frac{26}{9})^2]}.](https://mathovore.fr/latex-images/7fc68b97884ce68f70f2d82eec932359.png)
Déterminer l’équation de l’ensemble 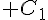 .
.
L’équation de cet ensemble est donc :
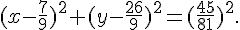
2. Montrer que c’est une médiatrice.
Exercice 9:
0. On place les points A(-2 ; 0), B(4 ; 0), C(2 ; 4) et D(0 ; 4) dans un repère orthonormé.
1. Pour montrer que ABCD est un trapèze isocèle, il faut montrer que les côtés parallèles sont de même longueur.
Le côté AB a pour longueur |4 – (-2)| = 6.
Le côté CD a pour longueur |2 – 0| = 2.
Donc les côtés AB et CD ne sont pas de même longueur. Ainsi, ABCD n’est pas un trapèze isocèle.
2. Pour que O soit le barycentre de 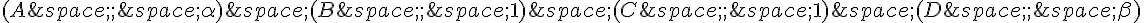 , on doit avoir les conditions suivantes :
, on doit avoir les conditions suivantes :
 (somme des coefficients égale à 0)
(somme des coefficients égale à 0)
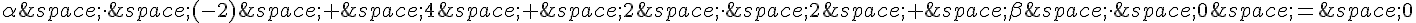 (somme des produits égale à 0)
(somme des produits égale à 0)
Cela donne le système d’équations suivant :
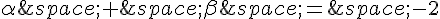
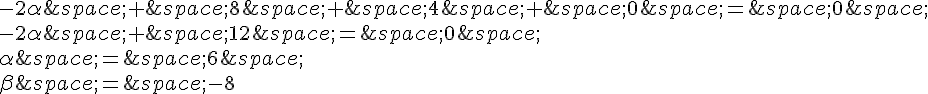
Donc 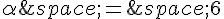 et
et 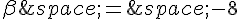 .
.
3.
a. On a 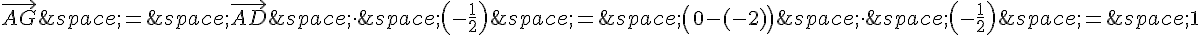 .
.
Donc G est le milieu de [AD], donc G a pour coordonnées  .
.
Pour que G soit le barycentre de (A ; a) (D ; b), on doit avoir les conditions suivantes :
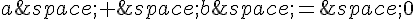 (somme des coefficients égale à 0)
(somme des coefficients égale à 0)
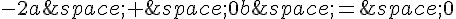 (somme des produits égale à 0)
(somme des produits égale à 0)
Cela donne le système d’équations suivant :
a + b = 0
-2a = 0
a = 0
b = 0
Donc a = 0 et b = 0.
b. Les coordonnées de I sont 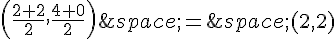 .
.
Pour que G, O et I soient alignés, il faut que les vecteurs 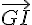 et
et 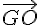 soient colinéaires.
soient colinéaires.
Le vecteur 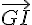 a pour composantes (2-2,2-2) = (0,0).
a pour composantes (2-2,2-2) = (0,0).
Le vecteur 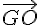 a pour composantes
a pour composantes 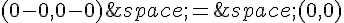 .
.
Donc 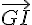 et
et 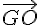 sont colinéaires et donc G, O et I sont alignés. O se trouve sur [GI].
sont colinéaires et donc G, O et I sont alignés. O se trouve sur [GI].
4.
a. Pour trouver les points M tels que 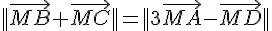 , on utilise la formule :
, on utilise la formule :
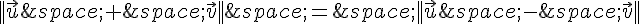
Donc 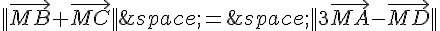 devient
devient 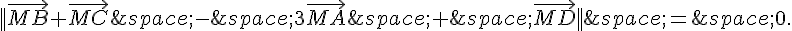
Calculons ces vecteurs :
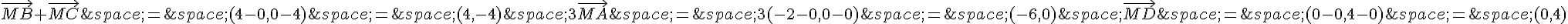
Donc l’équation devient 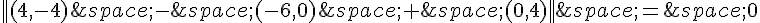 .
.
Simplifions cette équation :
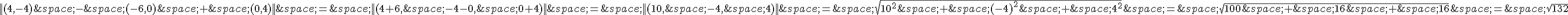
Donc l’ensemble E_1 des points M du plan tels que 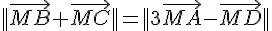 est le cercle de centre O et de rayon
est le cercle de centre O et de rayon 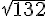 .
.
b. Pour montrer que O appartient à  , il suffit de vérifier que
, il suffit de vérifier que 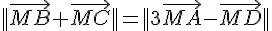 est bien satisfaite pour O.
est bien satisfaite pour O.
Calculons :
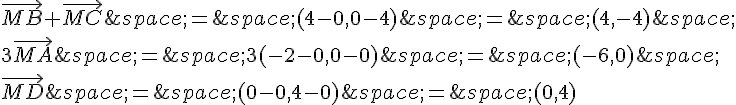
Donc 
Donc 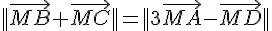 est bien satisfaite pour O, donc O appartient à E_1.
est bien satisfaite pour O, donc O appartient à E_1.
5.
a. Pour trouver les points M tels que 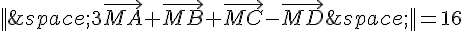 , on utilise la formule suivante :
, on utilise la formule suivante :
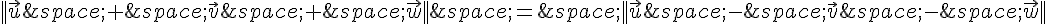
Donc 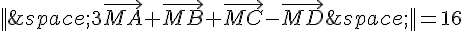 devient
devient 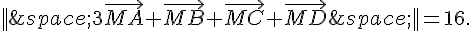
Calculons ces vecteurs :

Donc l’équation devient || (-6,0) + (4,0) + (2,4) + (0,4) ||=16.
Simplifions cette équation :
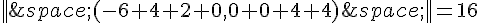 .
.
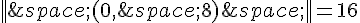 .
.
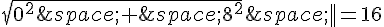 .
.
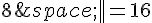 .
.
Cette équation n’est pas vérifiée car 8 n’est pas égal à 16.
Donc l’ensemble E_2 est l’ensemble vide car il n’y a pas de points M tels que 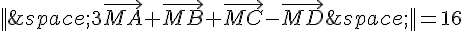 .
.
b. Pour montrer que B et D appartiennent à  , il faut vérifier que la condition
, il faut vérifier que la condition 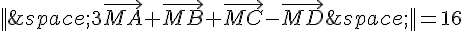 est satisfaite pour ces points.
est satisfaite pour ces points.
Calculons :

Donc
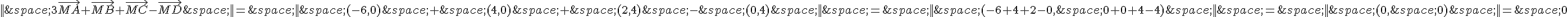 .
.
Donc la condition est vérifiée pour B et D, donc B et D appartiennent à E_2.
Exercice 10:
Voici une figure correspondant à la description donnée :
Effectuer la figure…
Pour démontrer que EDL est un triangle rectangle isocèle en E, il suffit de montrer que les longueurs des côtés DE et DL sont égales, et que l’angle DEL est droit.
1. Montrons que DE = DL :
Par construction, on sait que 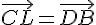 .
.
Cela signifie que les vecteurs CL et DB ont la même direction et la même norme.
La direction de ces vecteurs est déterminée par les droites AC et BD qui sont perpendiculaires à la base AB du triangle ABC.
Donc, CL et DB sont parallèles et ont la même norme. Donc, les longueurs des côtés DE et DL sont égales.
2. Montrons que l’angle DEL est droit :
Puisque CL et DB sont parallèles, les droites CE et DA sont également parallèles (par la propriété de Thalès dans le triangle ABC).
Donc, l’angle 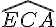 est égal à l’angle
est égal à l’angle 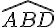 , et l’angle
, et l’angle 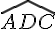 est égal à l’angle
est égal à l’angle  . Comme DBA est un triangle isocèle et rectangle en D et ACE est un triangle isocèle et rectangle en E, on a :
. Comme DBA est un triangle isocèle et rectangle en D et ACE est un triangle isocèle et rectangle en E, on a :
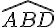 =
= 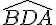 = 90 degrés et
= 90 degrés et  =
=  = 90 degrés.
= 90 degrés.
Donc, l’angle 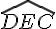 est égal à la somme des angles
est égal à la somme des angles 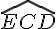 et
et 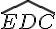 , qui est égale à 90 degrés.
, qui est égale à 90 degrés.
Donc, l’angle 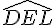 est droit.
est droit.
Ainsi, on a prouvé que EDL est un triangle rectangle isocèle en E.
Exercice 11 :
1.a. Pour trouver le point G qui est le barycentre du système de points pondérés 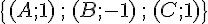 , on utilise la formule du barycentre :
, on utilise la formule du barycentre :
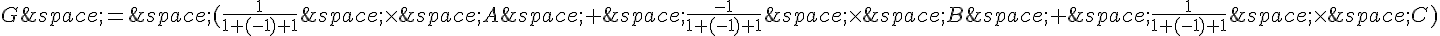
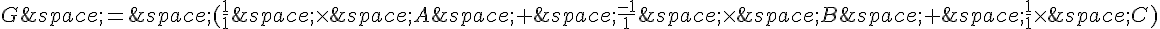
G = A – B + C
Donc le point G a pour coordonnées 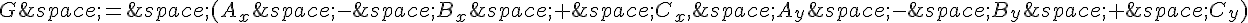 .
.
Il suffit de prendre les coordonnées de A, B et C pour trouver les coordonnées de G.
b. Pour trouver le point G’ qui est le barycentre du système de points pondérés 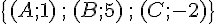 , on utilise la formule du barycentre :
, on utilise la formule du barycentre :
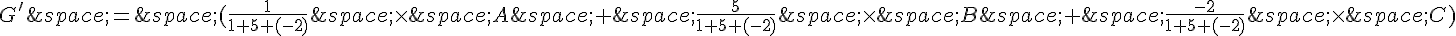
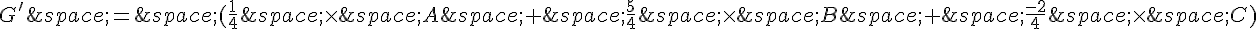
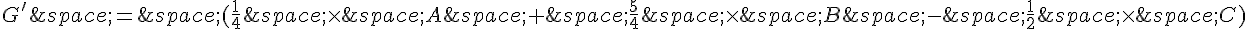
Donc le point G’ a pour coordonnées 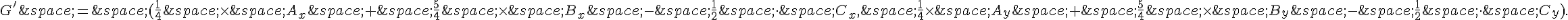
Il suffit de prendre les coordonnées de A, B et C pour trouver les coordonnées de G’.
2.a. Le point J est le milieu de [AB], donc les coordonnées de J sont
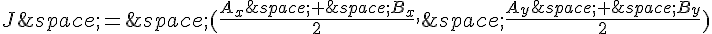 .
.
Les vecteurs 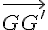 et
et 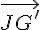 s’expriment en fonction de
s’expriment en fonction de  et
et 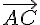 :
:
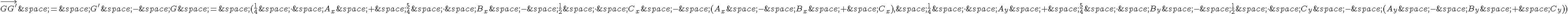
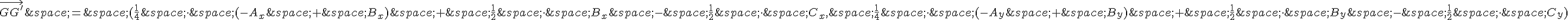

 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «barycentre : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.