DIPLÔME NATIONAL DU BREVET
ASIE PACIFIQUE
SESSION 2025
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points
Voici le sujet de mathématiques du brevet Asie Pacifique 2025, proposé aux élèves de troisième en série générale, suivi de son corrigé complet rédigé sous l’énoncé. L’épreuve dure deux heures, compte 100 points et se compose de cinq exercices indépendants qui balaient l’ensemble du programme du cycle 4.
Le premier exercice est un QCM : probabilité d’un tirage dans une urne, pourcentage, étendue, médiane et moyenne d’une série, lecture graphique d’une fonction affine. Puis le deuxième mobilise le théorème de Pythagore, le théorème de Thalès, l’aire d’un triangle rectangle et les triangles semblables. Ensuite, le troisième compare les périmètres d’un rectangle et d’un carré à l’aide d’un tableur, puis d’une équation du premier degré. Puis le quatrième demande de compléter des scripts Scratch pour tracer un hexagone, et le dernier traite de la décomposition en facteurs premiers, du volume d’un cylindre et d’un pavé droit, et d’une réduction en pourcentage.
Pour bien réviser, traitez l’épreuve en temps limité, calculatrice en mode examen, puis comparez votre copie avec la correction détaillée en bas de page : chaque réponse y est justifiée comme on l’attend le jour de l’examen.
Matériel autorisé :
L’usage de la calculatrice avec le mode examen activé est autorisé.
De plus, l’usage de la calculatrice sans mémoire, « type collège », est autorisé.
Ensuite, L’utilisation du dictionnaire est interdite.
Par ailleurs, le sujet est constitué de cinq exercices indépendants.
Puis le candidat peut les traiter dans l’ordre qui lui convient.
Exercice 1 : (16 points) (brevet 2025 Asie)
Cet exercice est un questionnaire à choix multiple (QCM).
Aucune justification n’est demandée.
Pour chaque question, quatre propositions (A, B, C et D) sont données.
Une seule est exacte. Recopier sur la copie le numéro de la question, ainsi que la lettre de la réponse.
Question 1 :
Dans une urne, on dispose de 4 boules bleues, 6 boules violettes, 7 boules rouges, 3 boules jaunes, toutes indiscernables au toucher. On tire une boule au hasard.
Quelle est la probabilité d’obtenir une boule violette ?
| Proposition A | Proposition B | Proposition C | Proposition D |
|---|---|---|---|
| \(\dfrac{6}{14}\) | \(\dfrac{1}{4}\) | \(\dfrac{3}{10}\) | \(\dfrac{14}{20}\) |
Question 2 :
Calculer 70 % d’une quantité revient à multiplier cette quantité par :
| Proposition A | Proposition B | Proposition C | Proposition D |
|---|---|---|---|
| 0,30 | 0,70 | 1,70 | 1,30 |
De même, question 3 :
On considère la série suivante composée de 5 valeurs : 7 ; 18 ; 12 ; 13 ; 15.
| Proposition A | Proposition B | Proposition C | Proposition D |
|---|---|---|---|
| L’étendue de cette série est 8 | La médiane de cette série est 12 | La moyenne de cette série est 53 | La moyenne de cette série est 13 |
Question 4 :
Une fonction affine f a pour représentation graphique la courbe C ci-dessous.
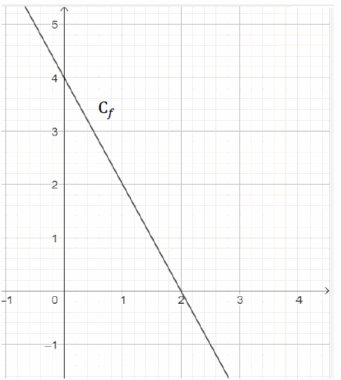
L’expression de la fonction f est :
| Proposition A | \(f(x)=2x+4\) |
|---|---|
| Proposition B | \(f(x)=4x-2\) |
| Proposition C | \(f(x)=-2x+4\) |
| Proposition D | \(f(x)=-4x+2\) |
Exercice 2 : (24 points)
Dans la figure ci-dessous qui n’est pas représentée en vraie grandeur :
• Les points G, C et E sont alignés.
• Les points F, C et D sont alignés.
• Les droites (GF) et (DE) sont parallèles.
• Le triangle CDE est rectangle en D.
• CD = 21,6 cm, CE = 29,1 cm et FC = 17,2 cm.
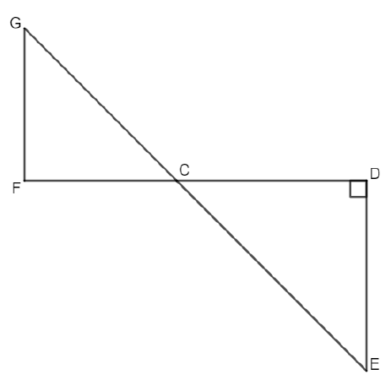
1) Montrer que la longueur DE est égale à 19,5 cm.
2) Calculer l’aire du triangle CDE.
3) Calculer la longueur GF arrondie au millimètre près.
4) On trace une droite (d) perpendiculaire à (FC) avec un logiciel de géométrie dynamique. La droite (d) coupe le segment [GC] en A et le segment [FC] en B.
En affichant l’aire du triangle ABC à l’aide du logiciel, on obtient 23,4 cm².
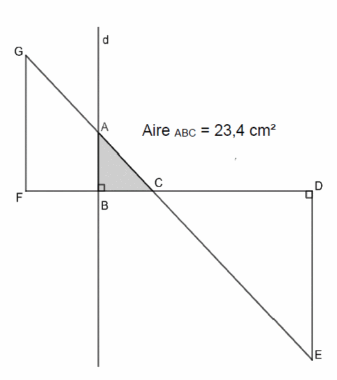
a. Montrer que l’aire du triangle ABC est égale à \(\dfrac{1}{9}\) de l’aire du triangle CDE.
b. On admet que les triangles ABC et EDC sont semblables.
Déterminer la longueur AB.
Exercice 3 : (20 points) (brevet 2025 Asie)
Dans cet exercice, toutes les longueurs sont exprimées en cm.
On considère :
• le rectangle ABCD tel que AD = \(x\) et AB = \(16-2x\) ;
• Le carré EFGH tel que EF = \(2x\).
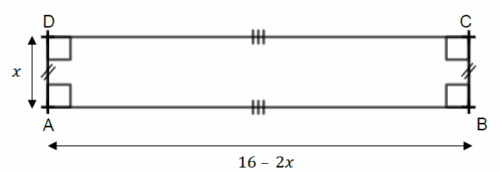
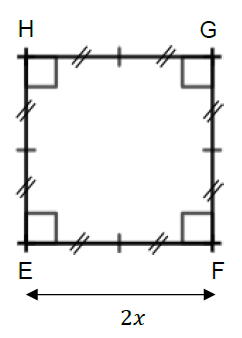
PARTIE A :
Dans cette partie, \(x=1{,}5\) cm.
1) Calculer le périmètre du carré EFGH.
2) Calculer AB.
3) Construire en vraie grandeur le rectangle ABCD.
4) Les périmètres de ABCD et EFGH sont-ils égaux ?
PARTIE B :
Dans cette partie, on cherche pour quelle(s) valeur(s) de \(x\) le périmètre du rectangle est égal au périmètre du carré.
1) Pour essayer de répondre au problème, on utilise la feuille de calcul suivante :
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | Valeur de \(x\) | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | Périmètre du carré | 8 | 16 | 24 | 32 | 40 | 48 |
| 3 | Périmètre du rectangle | 30 | 28 | 26 | 24 | 22 | 20 |
a. Quelle formule a-t-on pu saisir dans la cellule B2 avant de l’étirer jusqu’à G2 ?
b. Ce tableau nous permet-il de trouver une valeur de \(x\) pour laquelle les deux périmètres sont égaux ?
2) a. Montrer que le périmètre du rectangle peut s’écrire \(-2x+32\).
b. Déterminer la solution au problème par la résolution d’une équation.
Exercice 4 : (17 points)
Dans cet exercice, aucune justification n’est attendue.
Rappel :
L’instruction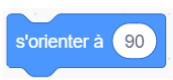 
PARTIE A :
Un élève souhaite tracer un hexagone à partir de 6 triangles équilatéraux comme sur la figure ci-dessous.
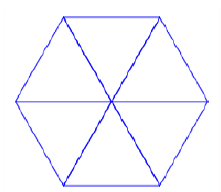
Pour cela, il commence par écrire le script ci-dessous du motif « triangle équilatéral ».
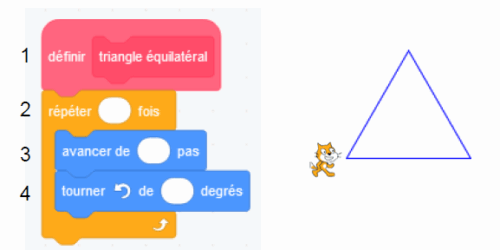
1) Compléter et recopier sur la copie les lignes 2, 3 et 4 du script pour que le lutin dessine un triangle équilatéral de côté 50 pas.
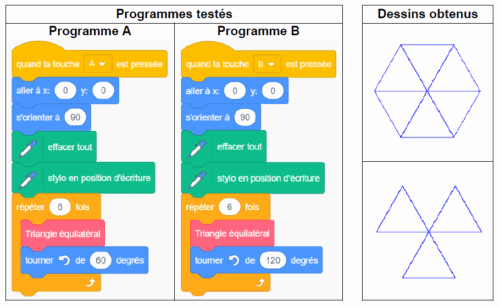
2) Cet élève teste les deux programmes A et B. Il obtient les deux dessins ci-dessous.
Quel programme permet de tracer l’hexagone souhaité ?
PARTIE B :
Un autre élève souhaite tracer un hexagone régulier de 50 pas de côté comme sur la figure ci-dessous.
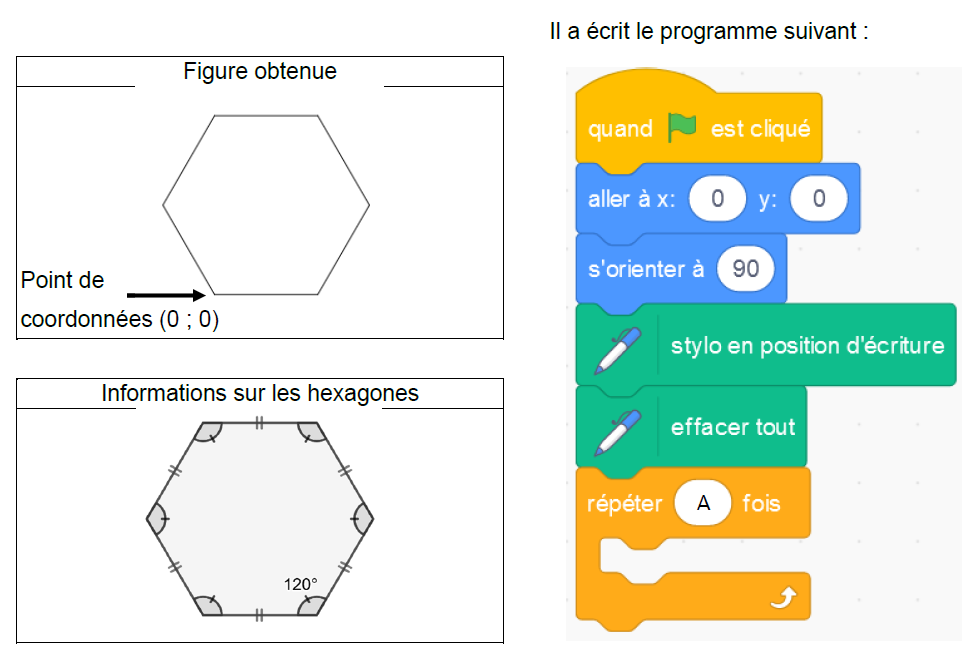
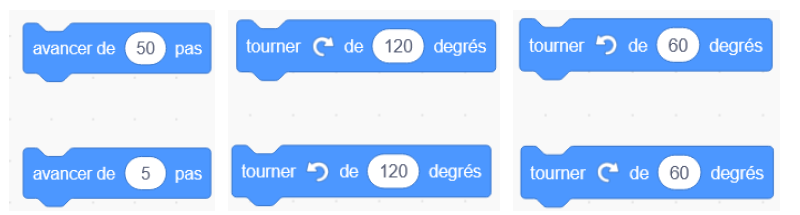
1) Sur la copie, recopier le bloc « répéter » en remplaçant A par sa valeur et en le complétant avec 2 instructions choisies parmi les 6 instructions proposées ci-dessous.
Exercice 5 : (23 points) (brevet 2025 Asie)
PARTIE A :
Un magasin a reçu 650 poissons dont 350 poissons de type A et 300 poissons de type B.
La responsable du magasin souhaite vendre ces poissons par lots de sorte que :
• le nombre de poissons de type A soit le même dans chaque lot ;
• le nombre de poissons de type B soit le même dans chaque lot ;
• tous les poissons soient répartis dans les lots.
1) Parmi les trois propositions suivantes, laquelle correspond à la décomposition en produits de facteurs premiers du nombre 300 ? Aucune justification n’est demandée.
| Proposition 1 | Proposition 2 | Proposition 3 |
|---|---|---|
| \(2^2\times 5\times 15\) | \(2\times 2\times 3\times 25\) | \(2^2\times 3\times 5^2\) |
2) Donner la décomposition en produit de facteurs premiers du nombre 350.
3) Quel nombre maximal de lots, la responsable du magasin pourra-t-elle constituer ?
4) Dans ce cas, combien y aura-t-il de poissons de chaque type dans chaque lot ?
PARTIE B :
Le magasin a d’autres poissons, appelés « poissons combattants ».
1) En captivité, il faut prévoir au moins 15 litres d’eau pour un poisson combattant.
Sachant qu’un aquarium se remplit au \(\dfrac{4}{5}\) de sa hauteur, lequel doit-on choisir pour un poisson combattant ?
- Aquarium 1 : cylindre, diamètre de la base : 30 cm, hauteur : 25 cm.
- Aquarium 2 : pavé droit, longueur : 28 cm, largeur : 28 cm, hauteur : 30 cm.
- Rappels : le volume d’un pavé droit est donné par la formule \(V=\text{Longueur}\times \text{Largeur}\times \text{Hauteur}\) ; le volume d’un cylindre de rayon de la base \(r\) est donné par la formule \(V=\pi\times r^2\times \text{Hauteur}\) ; \(1\text{ dm}^3=1\text{ L}\).
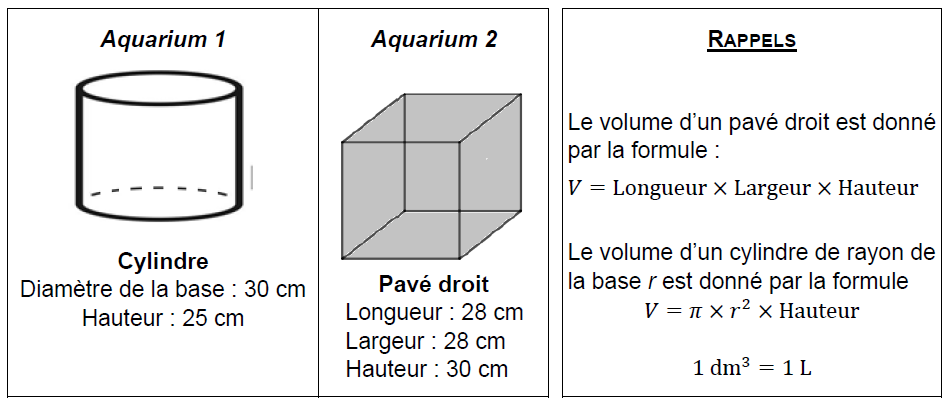
2) Le prix d’un poisson combattant est de 15 €.
Une famille achète un poisson combattant et un aquarium.
L’aquarium coûte 40 €.
Le vendeur fait une réduction de 15 % sur le prix total.
Combien va payer la famille ?
Voir le corrigé détaillé : Corrigé du brevet de maths 2025 en Asie-Pacifique
Bien travailler avec brevet 2025 Asie
Tout d’abord, fais l’exercice sans regarder la solution. Ensuite, compare ta démarche avec la correction, étape par étape. Ainsi, chaque erreur devient une occasion de progresser. De plus, un travail régulier sur brevet 2025 Asie vaut mieux qu’une longue séance.
Par exemple, refais un exercice raté deux jours plus tard. Enfin, le programme officiel de mathématiques est détaillé sur le site Éduscol. Également, tu peux continuer avec brevet Maths 2022 : sujet et corrigé à télécharger en PDF.
