Fonctions affines : exercices de maths en 3ème corrigés en PDF.
Mis à jour le 18 décembre 2025
Exercice 1
Expliquer ce que signifie les notations suivantes :
a. ;
b.
Exercice 2
Parmi les fonctions données, indiquer celles qui sont affines, celles qui sont linéaires, celles qui ne sont pas affines.
Exercice 3
La fonction f est définie par : .
a. Calculer f(2) ;f(- 3) ; f(0).
b. Calculer l’image de 4.
c. Calculer le nombre x tel que :
.
Exercice 4
On donne les images de deux nombres par une fonction affine f.
f(3)=5 et f(7)=13
a. Tracer sa représentation graphique dans un repère.
b. Déterminer l’expression algébrique de cette fonction (c’est-à-dire déterminer a et b).
Exercice 5
1. Dans un magasin, 100 g de chocolats sont vendus 3 €, et l’emballage coûte 1,52 €.
Sonia a acheté 750 g de chocolats et Samy en a achetés 900 g.
Combien chacun a-t-il payé ?

2. Deux personnes sont abonnées à un même ciné-club .
Pour trois séances, la première a payé 16 € (places et abonnement) ; pour cinq séances, la deuxième a payé 22 € ( places et abonnement).
Calculer le prix d’une place et le montant de l’abonnement.

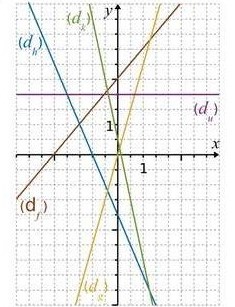
Exercice 6 – Déterminer des fonctions linéaires et affines
Sur le graphique ci-dessous, des fonctions f, g, h, k et u ont été représentées.
Déterminer chacune de ces cinq fonctions.
Exercice 7 – Représentation de fonctions linéaires et affines
Représenter les fonctions affines ci-dessous dans un même repère orthogonal avec des couleurs différentes.
Que peut-on dire des représentations graphiques des fonctions d et m ?
A votre avis quelle est la raison ?
Exercice 8 – Tarifs et abonnements
Yéro décide d’aller régulièrement à la piscine pendant un an.
Voici les tarifs proposés :
– tarif 1 : 100 € pour un an, nombre illimité d’entrées ;
– tarif 2 : 40 € d’adhésion par an puis 1 € par entrée ;
– tarif 3 : 2 € par entrée.
a. Quel prix paiera-t-il avec chaque tarif, s’il va à la piscine une fois par mois ? Quel tarif sera intéressant dans ce cas ?
b. On appelle x le nombre de fois où Yéro ira à la piscine.
Exprimer, en fonction de x :
t1(x) le prix qu’il paiera avec le tarif 1 ;
t2(x) le prix qu’il paiera avec le tarif 2
t3(x) le prix qu’il paiera avec le tarif 3.
c. Représenter graphiquement ces trois fonctions dans un même repère orthogonal.
d. En considérant qu’il y a 4 semaines pleines dans un mois :
Combien d’entrées Yéro devra-t-il payer s’il va à la piscine une fois par
semaine ?
Et s’il y va deux fois par semaine ?
e. Par lecture graphique, déterminer le tarif le plus intéressant pour Yéro dans ces deux cas.
f. À partir de combien d’entrées, Yéro aura t il intérêt à prendre un abonnement au tarif 1 (par lecture graphique)?
Exercice 9 – Images et antécédents
1)Soit la fonction affine f définie par f(x)= -2x+3 .
a) Calculer f(0) j’ai trouvé x=3.
b) Calculer l’antécédent de 5 .
2) Soit la fonction affine g telle que g(-2)=-2 et g(3)=4 .
a)Déterminer la fonction g .
b) Calculer g(0) et g(3) .
3) Dans un même repère (O,I,J).
a) Tracer les représentations graphiques de f et de g .
b) Calculer les coordonnées du point d’intersection de ces représentations graphiques .
Exercice 10 – Problème à résoudre
Pour le paiement de la garderie dans une école, on propose deux formules.
– Formule A : on paie 40 € pour devenir adhérent pour l’année scolaire puis on
paye 10 € par mois de garderie.
-Formule B : pour les non adhérents, on page 18 € par mois.
1. On appelle le nombre de mois de garderie.
On note A(x) le prix payé avec la formule A et B(x) le prix payé avec la formule B.
Exprimez A(x) puis B(x) en fonction de x.
2. Représentez graphiquement les fonctions suivantes dans un repère :
et
.
On prendra 1 cm pour 1 mois en abscisse et 1 cm pour 10 € en ordonnée.
3.
a) A partir du graphique, déterminer le nombre de mois pour lequel
les prix à payer sont les mêmes.
b) Retrouver ce résultat par le calcul.
4. A partir du graphique, déterminer la formule la plus avantageuse
si on ne paie que 4 mois dans l’année.
5. On dispose d’un budget de 113 €.
Combien de mois de garderie au maximum pourra-t-on payer
si l’on choisit la formule A ?
Exercice 11 – A la recherche de fonctions affines
Dans chacun des cas suivants, écrivez la fonction f sous la forme f(x)=ax+b
et précisez les valeurs de a et b.
1) La représentation graphique de f est une droite de coefficient directeur -3 et telle que f(0)=2.
2)La fonction f est la fonction qui, à un nombre x, lui ajoute 6 et multiplie le résultat par – 4.
3) La fonction f est la fonction qui, à un nombre x, le multiplie par 3, ajoute 4 au résultat,
puis divise le tout par 2.
4) La fonction f est définie par f(x)=(x+1)²-x².
5). La fonction f est telle que si les x augmentent de 3, les « f(x) » augmentent de 12.
De plus, f(0)=1.
Exercice 12 – Problème sur les volumes
Un horticulteur envisage la construction d’une serre entièrement
vitrée ayant la forme d’un parallélépipède rectangle surmonté
d’une pyramide comme l’indique la figure ci-après.
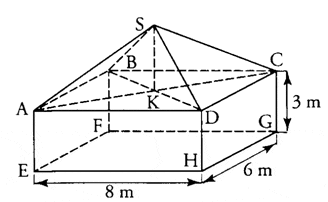
On désigne par la hauteur SK (exprimée en mètres) de la pyramide SABCD.
1) Montrer que le volume (en m3) de la serre est donné par la formule V = 144 + 16.
2) Calculer ce volume pour = 1,5.
3) Pour quelle valeur de le volume de la serre est-il de 200 m3 ?
Exercice 13 – Problème fonction affine et linéaire
Dans un magasin, une cartouche d’encre pour imprimante coûte 15 €.Sur un site internet, cette même cartouche coûte 10 e, avec des frais de livraison fixes de 40 € quel que soit le nombre de cartouches achetées.
1. Reproduire et compléter le tableau suivant :
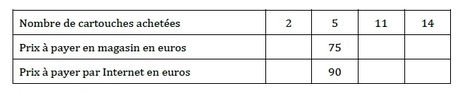
2. Le nombre de cartouches achetées est noté x.
a. On note le prix à payer pour l’achat de x cartouches en magasin.
Exprimer en fonction de x.
b. On note le prix à payer, en comptant la livraison, pour l’achat de x cartouches par internet.
Exprimer en fonction de x.
3. Dans un repère orthogonal (1 cm pour 1 unité en abscisse et 1 cm pour 10 unités en ordonnée) tracer les droites d et d’ définies par :
représente la fonction
représente la fonction
4. En utilisant le graphique précédent :
a. Déterminer le prix le plus avantageux pour l’achat de 6 cartouches.
Vous laisserez apparents les traits de construction.
b. Sonia dispose de 80 euros pour acheter des cartouches.
Est-il plus avantageux pour elle d’acheter des cartouches en magasin ou sur internet ?Vous laisserez apparents les traits de construction.
5. A partir de quel nombre de cartouches le prix sur internet est-il inférieur ou égal à celui du magasin ?
Expliquer votre réponse.
Exercice 14 – Achat d’un logiciel
L’école décide de tester un logiciel pour gérer sa bibliothèque. Elle télécharge ce logiciel sur
Internet.
1. Le fichier a une taille de 3,5 Mo (Mega-octets) et le téléchargement s’effectue en 7 secondes.
Quel est le débit de la connexion Internet ? On donnera le résultat en Mo/s.
Après une période d’essai de 1 mois, l’école décide d’acheter le logiciel.
Il y a trois tarifs :
• Tarif A : 19 €
• Tarif B : 10 centimes par élève
• Tarif C : 8 € + 5 centimes par élève
2. Compléter le tableau suivant :
| Nombre d’élèves | 100 | 200 | 300 |
| Tarif A | 19 € | ||
| Tarif B | 30 € | ||
| Tarif C | 18 € |
3. a. Si x représente le nombre d’élèves, laquelle des expressions suivantes correspond au tarif C ?
C1 = 8 + 5x
C2 = 8 + 0, 05x
C3 = 0, 05 + 8x
b. Est ce une situation de proportionnalité ? Justifier la réponse.
Exercice 15 – Vidéo club
Un vidéo-club propose différents tarifs pour l’emprunt de DVD :
-Tarif A : 5 € par DVD emprunté.
-Tarif B : 2,50€ par DVD emprunté, après avoir payé un abonnement de 18€.
-Tarif C : abonnement de 70€ pour un nombre illimité de DVD.
1. Recopier et compléter le tableau suivant :
|
5 DVD |
15 DVD |
25 DVD |
|
|
Coût au tarif A |
|||
|
Coût au tarif B |
|||
|
Coût au tarif C |
On note le nombre de DVD empruntés
2. Exprimer en fonction de :
le prix payé f() au tarif A ; le prix payé g(
) au tarif B et le prix payé h(
) au tarif C.
3. Représenter graphiquement, dans un repère orthogonal, les trois fonctions suivantes :
Echelle : axe des abscisses : 1 cm pour 2 DVD
axe des ordonnées : 1cm pour 5 €.
4. a) Résoudre l’équation 5= 2,5
+ 18
b) Interpréter le résultat.
5. a) Résoudre graphiquement l’inéquation suivante : .
b) Retrouver ensuite le résultat par le calcul.
6. Synthèse : donner le tarif le plus intéressant selon le nombre de DVD empruntés.
Exercice 16 – Calculs d’image et d’antécédents
est la droite représentative de la fonction h.
1. Donner un antécédent de – 3 par la fonction h.
2. Donner l’image de – 2,5 par la fonction h.
3. Tracer la droite représentative de la fonction
.
4. déterminer l’expression de la fonction représentée ci-dessous par la droite .
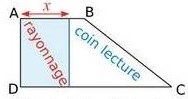
Exercice 17 – Le C.D.I
Le CDI du collège Evariste Galois a la forme d’un trapèze.
La documentaliste veut partager l’espace en deux parties de même aire,
l’une rectangulaire, de largeur x mètres avec des rayonnages pour ranger les livres, l’autre pour faire un coin lecture.
On donne AB= 5 m; AD = 10 m et DC = 8 m.
a. Calculer l’aire totale du CDI.
b. Quelles sont les valeurs possibles pour x ?
c. Exprimer, en fonction de x, r(x) l’aire de l’ espace rayonnage et c(x) l’aire de l’espace coin lecture en .
d. Représenter, par lecture graphique, la valeur de x pour laquelle les voeux de la documentaliste seront pris en compte.
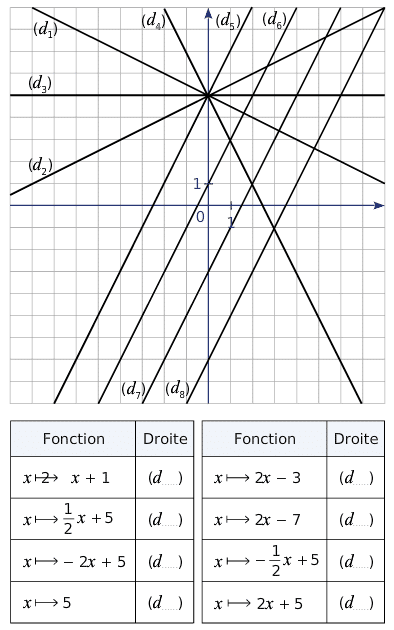
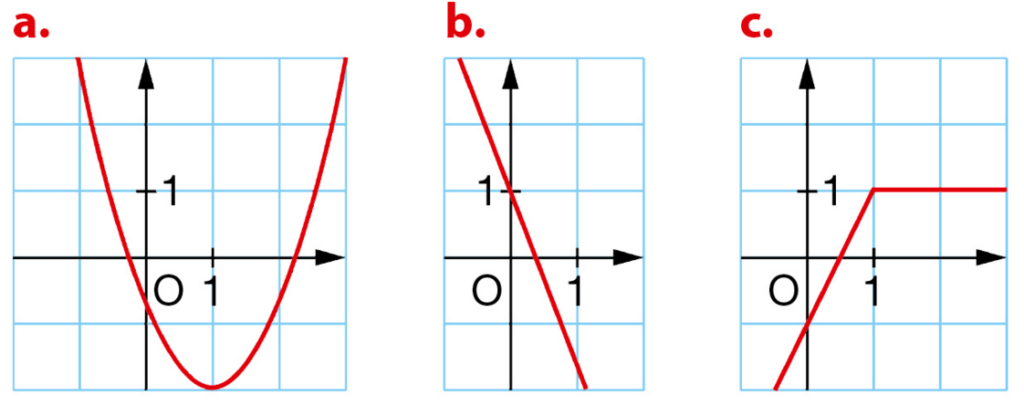
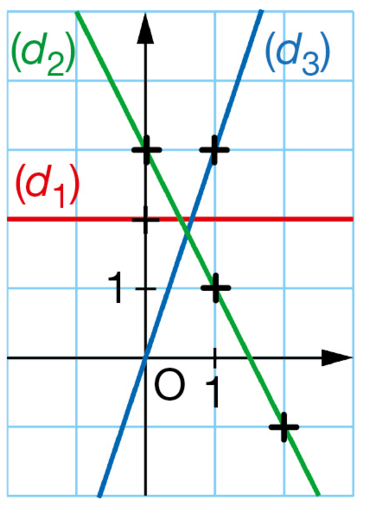
Exercice 18 :
Par lecture graphique, indiquer pour chaque fonction affine, quelle droite est sa représentation graphique.
Exercice 19 :
Déterminer la fonction affine f telle que f(9)=-1 et f(18)= – 8.
Exercice 20 :
f est la fonction affine définie par : .
a. Calculer l’image de —4 par f.
b. Déterminer l’antécédent de 5 par f.
Exercice 21 :
g est la fonction affine définie par :
.
1. Calculer l’image par g de:
a. 2 b.0 c.-8
2. Déterminer l’antécédent par g de:
a.0 b.9 c.—1
Exercice 22 :
h est la fonction affine .
Recopier et compléter le tableau suivant :
Exercice 23 :
g est la fonction affine .
Amar affirme : « L’image d’un nombre par g est toujours négative. »
Que peut-on en penser ? Expliquer.
Exercice 24 :
f est la fonction affine .
Quel programme de calcul faut-il appliquer :
a. pour calculer l’image d’un nombre par f?
b. pour déterminer l’antécédent d’un nombre par f?
Exercice 25 :
Voici des fonctions affines.
Pour chacune d’elles, préciser les valeurs de a et de b.
Exercice 26 :
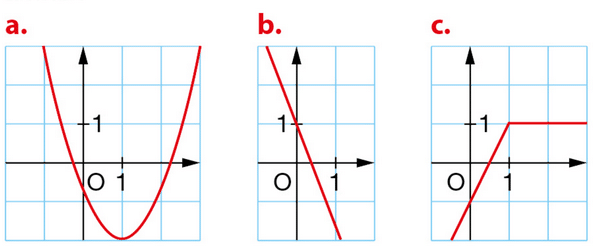
Le graphique peut-il représenter une fonction affine ?
Exercice 27 :
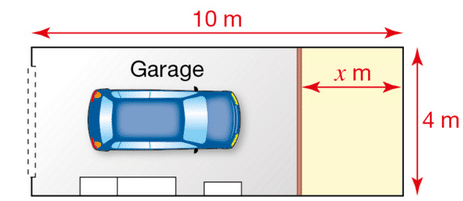
Louise a un garage rectangulaire de 10 m sur 4 m.
Elle veut installer une cloison pour avoir un débarras au fond de son garage comme indiqué ci-dessous.
On note l’aire, en m², de la surface de garage dont elle disposera après l’installation de la cloison.
1. Donner l’expression de .
2. a. Déterminer :
et l’antécédent de 32.
b. Que signifient ces résultats pour la situation ?
Exercice 28 :
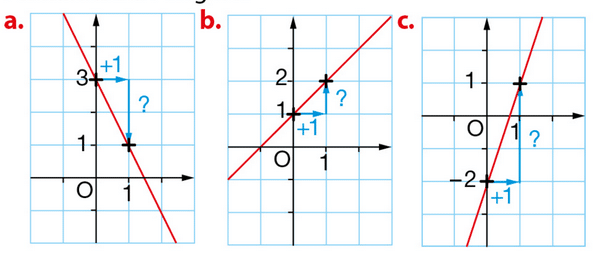
Les droites ci-dessous représentent graphique ment des fonctions affines.
Dans chaque cas, lire le coefficient directeur et l’ordonnée à l’origine.
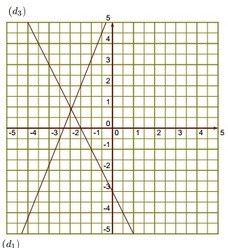
Exercice 29 :
Voici trois applications affines définies par :
f(x) = 36 ; g(x) = 1,2+ 12 ; h(x) = 2,4.
1) Calculer g(5) et h(5).
2) Sur une feuille de papier millimétré, dans un repère orthogonal, avec 1 cm pour 2 unités sur l’axe des abscisses et 1 cm pour 3 unités sur l’axe des ordonnées, tracer les droites d1, d2 et d3 associées respectivement aux applications affines définies par f(x), g(x) et h(x).
3) Déterminer par le calcul les valeurs de pour lesquelles g(x) < f(x).
4) Calculer les coordonnées du point M, intersection des droites d1 et d2, et les coordonnées du point N, intersection des droites d2 et d3.
Exercice 30 :
I – Le plan est muni d’un repère orthogonal.
(Utiliser une feuille de papier millimétré.)
Prendre sur l’axe des abscisses 2 cm pour une unité.
Prendre sur l’axe des ordonnées 1 cm pour 20 unités.
Graduer l’axe des abscisses de 0 à 5.
Graduer l’axe des ordonnées de 0 à 270.
1) Tracer dans ce repère les droites D1, D2 et D3 d’équations :
D1 : y = – 90x + 270 (en bleu)
D2 : y = – 40x + 150 (en rouge)
D3 : y = – 10x + 50 (en noir)
(Donner les coordonnées de 2 points pour chaque droite.)
2) Calculer les coordonnées de M, point d’intersection de D1 et de D2.
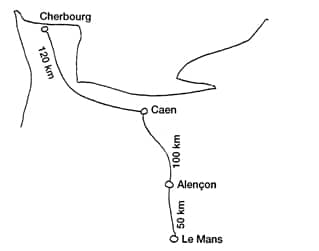
II – Le samedi 18 juin 1995, à 16 h, a été donné le départ de la course automobile des 24 heures du Mans.
Les 3 personnes suivantes s’y sont rendues :
- · Hélène est partie de Cherbourg avec sa voiture et a roulé à la vitesse moyenne de 90 km/h.
- · Clément est parti de Caen avec son scooter et a roulé à la vitesse moyenne de 40 km/h.
- · Adrien est parti d’Alençon à vélo et a roulé à la vitesse moyenne de 10 km/h.
La distance de Cherbourg à Caen est de 120 km. Celle de Caen à Alençon est de 100 km. Celle d’Alençon au Mans est de 50 km.
Les trois personnes ont quitté leur domicile à 8 heures.
On désignera par le temps, en heures, écoulé après 8 heures et par la distance, en km, restant à parcourir pour arriver au Mans.
1) a) Quelle distance Hélène parcourt-elle en heures ?
b) En déduire que, après heures de trajet, la distance qu’il lui reste à parcourir pour arriver au Mans est égale à 270 – 90x.
On notera H(x) = 270 – 90x.
2) Après heures de trajet, quelle distance doit encore parcourir Clément pour arriver au Mans ? On notera cette distance C(x).
De même, après heures de trajet, quelle distance doit encore parcourir Adrien pour arriver au Mans ? On notera cette distance A(x).
3) Quelle interprétation peut-on donner des coordonnées du point M considéré dans la partie I-2) ?
4) Par une lecture du graphique, estimer à quelle distance du Mans, Hélène doublera Adrien. Estimer l’heure de ce dépassement.
5) Par un calcul, déterminer à quelle heure et à quelle distance du Mans Clément doublera Adrien.
Exercice 31 :
Deux villes A et B sont distantes de 92 km.
Un motocycliste part de A et se dirige vers B à la vitesse de 54 km/h.
Au même moment, un automobiliste quitte la ville B pour se rendre en A : il roule à la vitesse de 84 km/h. (Ces vitesses sont supposées constantes durant tout le trajet.)
(Formule : distance parcourue = vitesse x durée du parcours.)
I – 1) a) A quelle distance de la ville A se trouve le motocycliste 10 minutes après son départ ? une demi-heure après son départ ? 40 minutes après son départ ?
b) A quelle distance de la ville A se trouve l’automobiliste 10 minutes après son départ ? une demi-heure après son départ ? 40 minutes après son départ ?
2) Montrer que 54 km/h = 0,9 km/min.
De la même façon, exprimer 84 km/h en km/min.
3) a) Le motocycliste a roulé pendant minutes. Exprimer à l’aide de la distance le séparant de la ville A.
b) L’automobiliste a également roulé pendant minutes. Montrer que la distance le séparant de la ville A est égale à 92 – 1,4x .
c) En déduire l’instant où les deux véhicules vont se croiser.
Il – Le plan est muni d’un repère orthogonal.
Sur l’axe des abscisses, où sont repérées les durées, 1 cm représente 10 minutes.
Sur l’axe des ordonnées, où sont repérées les distances, 1 cm représente 10 kilomètres.
1) Tracer la droite (D1) d’équation = 0,9, puis la droite (D2) d’équation = – 1,4x + 92.
2) Les droites (D1) et (D2) se coupent en P. Calculer les coordonnées de P
Que représentent les coordonnées de ce point P ?
3) La droite (D2) coupe l’axe des abscisses en Q.
Lire l’abscisse de Q.
Que représente ce nombre ?
Exercice 32 :
f est la fonction affine .
Quel programme de calcul faut-il appliquer :
a. pour calculer l’image d’un nombre par f?
b. pour déterminer l’antécédent d’un nombre par f?
Exercice 33 :
Le graphique peut-il représenter une fonction affine ?
Exercice 34 :
Dans ce repère, les droites (), (
) et (
) représentent
graphiquement les fonctions affines respectives et
.
1. Parmi ces fonctions, laquelle est linéaire ? constante ?
2. Par chaque fonction, donner :
a. l’image de 1.
b. si possible, l’antécédent de 3.
Exercice 35 :
Un site de stockage de données en ligne propose l’offre suivante :
On note f la fonction qui modélise le montant, en euros, d’une commande de x gigaoctets.
a. Donner l’expression de f(x).
La fonction f est-elle affine ?
b. Calculer l’image de 400 par la fonction f.
Interpréter le résultat pour la situation.
c. Déterminer l’antécédent de 15 par la fonction f.
Interpréter le résultat pour la situation.
Exercice 36 :
Voici le devis établi par un couvreur-zingueur pour refaire la
toiture en tuiles d’une maison.
1.Exprimer le coût pour refaire une toiture de x m².
2.a. Déterminer :
- C(120)
- l’antécédent de 4 500.
b. Que signifient ces résultats pour la situation ?
Exercice 37 :
Effectuer le QCM sur les fonctions affines suivant :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions affines : exercices de maths en 3ème corrigés en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.