Les équations : exercices de maths en 3ème corrigés en PDF.
Mis à jour le 19 décembre 2025
Exercice 1 – Résoudre ces équations du premier degré
Résoudre les équations suivantes :
a) x + 0,6 = 4,8
b) -2 + x = 5
c) -2x = 5
d) -3+x = -9
e) -6x = -8
f) 4x + 5 = 0
g) 9 – 3x = 0
h) 4 + 2x = 10 – 4x
i) 9x – 7 = 3 – 3x + 8
j) 3x + 1 = 2x – 2
k) 5x + 10 = 3x + 40
l) 4 + 2x = 20 – 8x
m) 2 ( 3x – 1 ) – 2x = 7x + 3
n) 10x – 5 – 3 ( 2x + 5 ) = -20
Exercice 2 – Trouver trois nombres consécutifs
Déterminer trois nombres entier positifs consécutifs dont la somme des carrés est égale à 1 325.
Exercice 3 – Clubs et médailles
Trois club se rencontrent lors d’une compétition. Le club A remporte un tiers des médailles , le club B deux septième des médailles et le club C seize médailles . Combien de médaille ont été distribuée en tout ?
Exercice 4 – Résoudre les équations
1. (x-7)²-(2x+5)²=0
2. (7x+1)²-(3x+4)²=0
3. (6x-1)²-(2x+1)²=0
Exercice 5 – Pièces en euros
Une tirelire contient 65 euros en pièces de 1 € et 2 € au total de 35 pièces .
Combien y a t il de pièces de 1 euros et combien de 2 euros ?
Exercice 6
Résoudre les équations suivantes :
a. 3x + 2 = 14 ;
b. 3x – 4 = 2x + 9 ;
c. 5x – 4 = 8 – 3x ;
d. 3 – (5 – x) = 3 – 4x ;
e. 2x + 5 = 3x – 1 ;
f. 2(5 – 3x) = 6(2x + 1) ;
g. 4(3x – 2) – 10x = 3x – 1 ;
h. 3(x + 2) – (x – 3) = x – 5 – 3(x + 1) + 4x ;
i. 5x + 7 = -5 + 11x ;
j. 2x + 1 = 4(x – 2) + x ;
Exercice 7
Résoudre l’équation suivante :
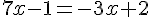
Exercice 8
Résoudre les équations suivantes:
1. (x + 5)(x – 3) = 0
2. ( 2x + 7 )( -5x + 2 ) =0
3. 64x² – 81 = 0
5. ( 3 – x )(2x + 7 )(-5 + x) = 0
6. 49x² – 42x + 9 = 0
Exercice 9
Trouver les équations qui admettent ( 2 ) pour solution:
1. 2x + 4 = 0
2. 2x = – 4
3. 6x + 2 = 10
4. 5x + 4 = 2x+3
Exercice 10
Quand Julie est née, sa mère était âgée de 30 ans et son frère avait 4 ans.
Aujourd’hui, ensemble, Julie, son frère et sa mère totalisent un siècle (100 ans).
1. Si on appelle x l’âge de Julie, exprimer l’âge de son frère et de sa mère en fonction de x.
2. Quel est l’âge de Julie ?
Exercice 11
1) 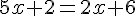
2) 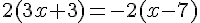
3) 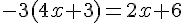
4) 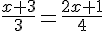
5) 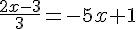
6) 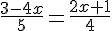
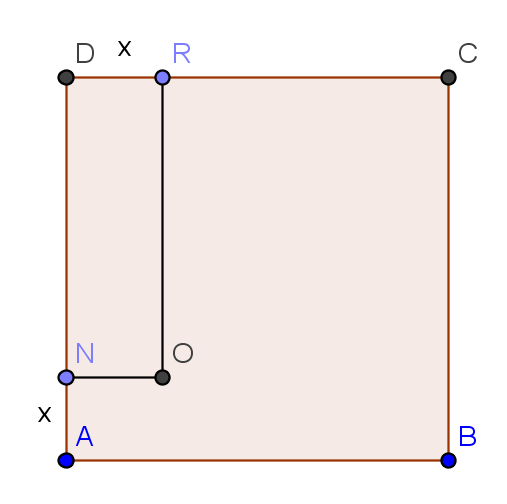
Exercice 12 – Etude d’un carré
Soit ABCD est un carre de cote 10 cm .
N est un point de [AD] et R est un point de [DC] tels que AN est égal à DR est égal a x (en cm).
on souhaite trouver la position du point N pour laquelle l ‘aire du rectangle NORD est maximale .
1) Donner un encadrement de x.
2)a) Exprimer l’aire de NORD en fonction de x.
b) Démontrer que l ‘aire est égale à : 25-(x-5)².
3)a) Déterminer la valeur de x pour laquelle l aire NORD est maximale ou est alors situé le point N .
b) Dans ce cas que peut on dire du rectangle NORD .
Exercice 13
Résoudre les équations suivantes :
a. 3x + 2 = 14 ;
b. 3x – 4 = 2x + 9 ;
c. 5x – 4 = 8 – 3x ;
d. 3 – (5 – x) = 3 – 4x ;
e. 2x + 5 = 3x – 1 ;
f. 2(5 – 3x) = 6(2x + 1) ;
g. 4(3x – 2) – 10x = 3x – 1 ;
h. 3(x + 2) – (x – 3) = x – 5 – 3(x + 1) + 4x ;
i. 5x + 7 = -5 + 11x ;
j. 2x + 1 = 4(x – 2) + x ;
Exercice 14
Résoudre l’équation suivante :
Exercice 15
Résoudre les équations suivantes:
1. (x + 5)(x – 3) = 0
2. ( 2x + 7 )( -5x + 2 ) =0
3. 64x² – 81 = 0
5. ( 3 – x )(2x + 7 )(-5 + x) = 0
6. 49x² – 42x + 9 = 0
Exercice 16
Trouver les équations qui admettent ( 2 ) pour solution:
1. 2x + 4 = 0
2. 2x = – 4
3. 6x + 2 = 10
4. 5x + 4 = 2x+3
Exercice 17
Quand Julie est née, sa mère était âgée de 30 ans et son frère avait 4 ans.
Aujourd’hui, ensemble, Julie, son frère et sa mère totalisent un siècle (100 ans).
1. Si on appelle x l’âge de Julie, exprimer l’âge de son frère et de sa mère en fonction de x.
2. Quel est l’âge de Julie ?
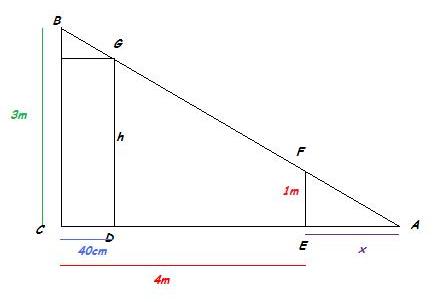
Exercice 18 – Thalès et résolution d’équations
Déterminer la valeur de la longueur x.
Exercice 19 – Equations produits à résoudre
Résoudre les équations suivantes après avoir factoriser a l’aide d’une identité remarquable:
a) x² +14x+49=0
b) y²-12y+36=0
c) 4x²-20x +25=0
d) 24z+16+9z²=0
Exercice 20 – Problème de factorisation
1) Factoriser E = 4x²-49
2) Soit l’expression F= (2x-7)(-5x+9)+4x²-49 .
a) développer puis réduire F.
b)calculer la valeur exacte de F lorsque 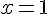 ,
, 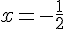 ,
,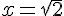 .
.
c)écrire F sous forme d’un produit de facteurs du premier degré .
d)résoudre l’équation F=0 .
Exercice 21 – Développement, factorisation et équation de produit nul
On donne l’expression A= (2x-3)²-(4x+7)(2x-3) .
1. Développer et réduire A.
2. Factoriser A .
3. Résoudre l’équation (2x-3)(-2x-10)= 0
Exercice 22 – Problème du boulanger
Un boulanger vend les deux tiers de ses baguettes le matin.
L’après-midi, il en vend encore 90.
Le soir, il lui reste 20 baguettes.
Combien avait-il cuit de baguettes pour la journée ?
Exercice 23 – Calcul littéral
Les deux questions suivantes sont liées .
1) Développez 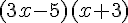 .
.
2) Résolvez l’équation  .
.
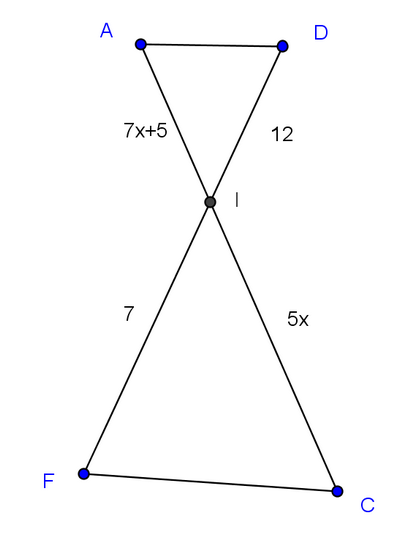
Exercice 24 – Equations et théorème de Thalès
On considère les points A,I et C alignés dans cet ordre et les points D,I et F alignés dans cet ordre.
On donne
IF = 7
IC = 5x
IA = 7x + 5
ID = 12.
Déterminer la valeur de x pour laquelle les droites (FC) et (DA) sont parallèles.
Exercice 25 :
Trouver 3 nombres entiers consécutifs dont la somme est égale à 984.
On posera comme inconnue le plus petit nombre.
Exercice 26 :
Un club de sport propose la formule suivante : une carte d’adhérent de 12 € puis
l’utilisation de la salle de gymnastique facturée 4,50 € l’heure.
Désignons par x le nombre d’heure d’utilisation de la salle de gymnastique.
Déterminer le prix à payer en fonction du nombre d’heure d’utilisation.
Au bout de combien d’heure d’utilisation le prix à payer est de 79,50 € ?
Exercice 27 :
Le réservoir d’une voiture est plein au un tiers. On rajoute 42 litres pour le remplir.
Quelle est sa contenance ?
On choisira comme inconnue la contenance totale du réservoir.
Exercice 28 :
Un troupeau est composé de chameaux et de dromadaires. On compte 180 têtes et 304 bosses.
Sachant qu’un dromadaire a une bosse et un chameau 2, combien y a-t-il d’animaux de chaque espèce ?
Exercice 29 :
Résoudre les équations suivantes :
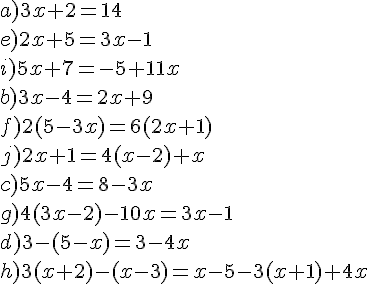
Exercice 30 :
Résoudre les équations produit suivantes:
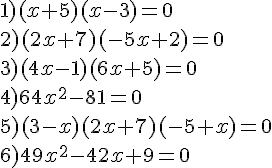
Exercice 31 :
Trouver les équations qui admettent ( 2 ) pour solution:
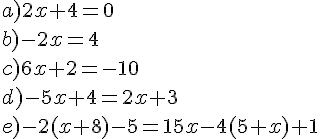
Exercice 32 :
Pierre achète 8 pin’s de même prix. Luc achète 10 pin’s qui valent chacun 5 € de moins que ceux de Pierre.

a) Si x est le prix d’un pin’s acheté par Pierre, quel est le prix d’un pin’s acheté par Luc ?
b) Quel est le montant de l’achat de Pierre ?
c) Quel est le montant de l’achat de Luc ?
d) Sachant que Pierre et Luc ont dépensé la même somme, quel est le prix d’un pin’s de Pierre ?
Exercice 33 :
Quand Julie est née, sa mère était âgée de 30 ans et son frère avait 4 ans.
Aujourd’hui, ensemble, Julie, son frère et sa mère totalisent un siècle (100 ans).
a) Si on appelle x l’âge de Julie, exprimer l’âge de son frère et de sa mère en fonction de x.
b) Quel est l’âge de Julie ?
Exercice 34 :
Dans la cour de la ferme, il y a des poules (elles ont deux pattes !) et des lapins (ils ont quatre pattes !). J’ai compté 40 têtes et 106 pattes.

Combien y a-t-il de poules et de lapins ?
Exercice 35 :
Yaël achète quatre roues et un grip à 15 € pour son skate.
Elle donne un billet de 50 € ; le vendeur lui rend 3 €.
Quel est le prix de chaque roue ?
Exercice 36 :
La formule ci-dessous donne le coût, en €, de location d’une planche de surf en fonction du
nombre d’heures où on la loue.
Coût = 25 x nombre d’heures + 10
Pendant combien d’heures Hugo a-t-il loué une planche s’il a payé 60 € ?
Exercice 37 :
Résoudre chaque équation.
a. 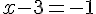
b. 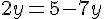
c. 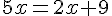
d. 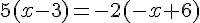
Exercice 38 :
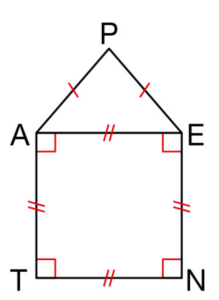
AENT est un carré dont le périmètre est 56 cm.
PAE est un triangle isocèle en P.
a. Calculer AE.
b. Pour quelle longueur de [AP] le périmètre du pentagone PENTA est-il
égal à 60 cm ? Justifier.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les équations : exercices de maths en 3ème corrigés en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.