Trigonométrie : exercices de maths en 3ème corrigés en PDF.

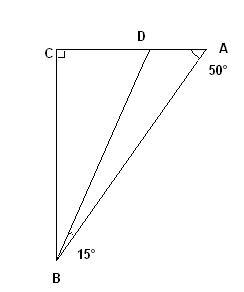
Exercice 1 – Périmètre
on sait que    ;  ;  et  .
Calculer le périmètre du triangle ABD Donner l’arrondi du résultat au décimètre près.

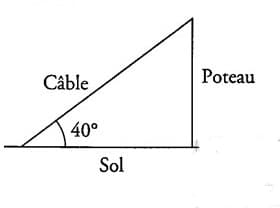
Exercice 2 – Câble
Un câble de 20m de long est tendu entre le sommet d’un poteau vertical et le sol horizontal.
Il forme un angle de 40° avec le sol.
a) Calculer la hauteur du poteau; donner la valeur approchée au dixième près par défaut.
b)Représenter la situation par la figure à l’échelle 1/200. (Les données de la situation doivent être placées sur la figure.)

Exercice 3 – Calculatrice
1.a. A l’aide de la calculatrice, calculer  (cos67°+sin67°)²+(cos67°-sin67°)² (cos35°+sin35°)²+(cos35°-sin35°)² b. Que constate-t-on?

2.Démontrer que pour tout angle aigu x : (cos x+sin x)²+(cos x-sin x)²= 2.

Exercice 4 – Triangle rectangle et trigonométrie
Démontrer que le triangle SON est rectangle.

Exercice 5 – Calcul de la tangente et du cosinus
 est un angles tel que  .

En utilisant les formules trigonométriques , calculer les valeurs exactes de  et   .

Exercice 6 – Cercle circonscrit
1. Construisez un triangle ABC rectangle en C tel que AC = 5 cm et .

2. Calculez la longueur BC.(On donnera une valeur arrondie au millimètre).

3.a) Où se trouve le centre O du cercle circonscrit au triangle ABC?Justifiez.

b) Tracez  ce cercle.

4. Déduisez-en la mesure de l’angle .

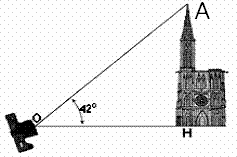
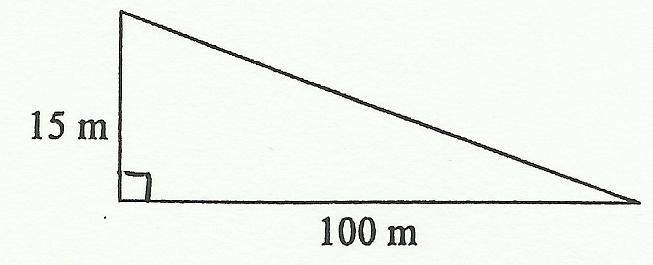
Exercice 7 – Mesure de la hauteur d’une cathédrale
 Cette cathédrale mesure 140 m de haut.

L’appareil photo est muni d’un objectif dont l’angle d’ouverture est 42°.

Quelle est la distance OH nécessaire pour que la cathédrale apparaisse entièrement dans l’objectif ?

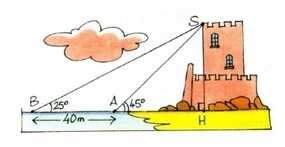
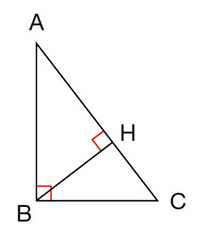
Exercice 8 – Trigonométrie dans le triangle rectangle.

On sait que AB = 40 m,  et .

On cherche la hauteur SH du donjon.

On pose x = Sh (avec x exprimé en m).

a. Exprimer BH en fonction de x.

b. Exprimer AH en fonction de x.

c. Sachant que AB = 40 m, écrire une équation dont l’inconnue est x.

d. Résoudre l’équation et donner la hauteur du donjon en arrondissant au mètre le plus proche.

La série 3 des exercices sur la trigonométrie dans le triangle rectangle en 3ème. Ces exercices corrigés dans les détails portant sur le cosinus, sinus et la tangente d’un angle sont à télécharger gratuitement en PDF en troisième.

Exercice 9 – Cube et trigonométrie

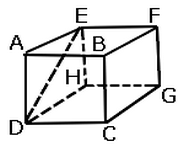
Dans le pavé droit ci-dessus, on donne EH=69 cm, EF=60 cm et EA=51 cm.
Quelle est la mesure de l’angle AED? (arrondir le résultat a l’unité)

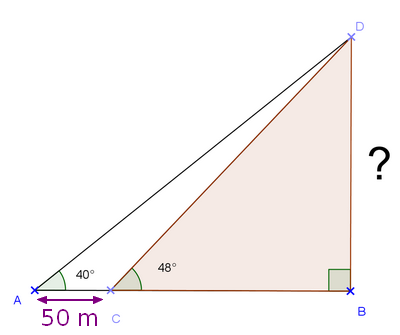
Exercice 10 – Mont-Saint-Michel et trigonométrie
Pour savoir à quelle hauteur culmine l’archange Saint Michel

situé au sommet de l’abbaye du Mont-Saint-Michel, Lisa utilise un théodolite

afin de mesurer des angles à partir de la baie.

Elle effectue une première mesure et observe le sommet de l’abbaye sous un angle de 48°.

Puis elle recule de 50 m et effectue une nouvelle mesure.

Elle voit alors le sommet de l’abbaye sous un angle de 40°.

Son père lui dit qu’elle peut maintenant trouver la hauteur du sommet de l’abbaye.

Aider Lisa à faire ce calcul en s’aidant du schéma ci-dessous :

Exercice 11 –  Formule d’Al-kashi
1. Construire en vraie grandeur un triangle ABC tel que : AB = 7 cm ; BC = 8 cm et AC = 5 cm.

2. Le triangle ABC est-il rectangle ? Justifier.

3. Le célèbre mathématicien Al-Kashi (XIV- XVème siècle) a trouvé une formule entre les trois
côtés d’un triangle et le cosinus de l’un des trois angles de ce triangle :

« Dans un triangle, qu’il soit rectangle ou non, on a :
. »

En utilisant la formule d’Al-Kashi, trouver la mesure arrondie au degré près de l’angle .

Exercice 12 – Pente d’une route et autoroute
Une pente de 15 % signifie que, pour un déplacement horizontal ,on se déplace verticalement de 15 m comme schématisé ci-dessous.

1) Dans le cas d’une pente à 15 %, quel angle fait la route avec l’horizontale?

2) On considère une descente dangereuse dès que la pente est supérieure à 10 % sur route et supérieure à 4 % sur autoroute.

A partir de quel angle entre chaussée et l’horizontale, considère-t-on qu’une descente est dangereuse sur route?sur autoroute?

3)Est-il plus dangereux de circuler sur une route qui a une pente de 20 % ou de rouler sur une autoroute faisant un angle de 20 degré avec l’horizontale ? Justifier

La série 4 des exercices sur la trigonométrie en 3ème avec le cos, sin et tan d’un angle aigu dans un triangle rectangle. Ces exercices en troisième disposent de leur correction détaillée et peuvent être téléchargés et imprimés en PDF.

Exercice 13

1. Construire un triangle IJK tel que :

JK = 8 cm ; IJ = 4,8 cm ; KI = 6,4 cm.

2. Démontrer que le triangle IJK est un triangle rectangle.

3. Calculer la mesure en degrés de l’angle .

Donner la valeur arrondie au degré le plus proche.

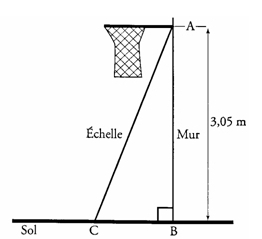
Exercice 14

1. Paul veut installer chez lui un panier de basket.

Il doit le fixer à 3,05 m du sol.

L’échelle dont il se sert mesure 3,20 m de long.

À quelle distance du pied du mur doit-il placer l’échelle pour que son sommet soit juste au niveau du panier ?

(Donner une valeur approchée au cm près.)

2. Calculer l’angle formé par l’échelle et le sol. (Donner une valeur approchée au degré près.)

Exercice 15

Soit ABC un triangle isocèle de base [BC], [AH] la hauteur issue du sommet A.

On a : BC = 8 cm et AH = 7 cm.

1. Construire le triangle ABC en justifiant la construction.

2. Calculer tan(B) .

3. En déduire la valeur de l’angle  arrondie au degré près.

Exercice 16

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

1. Dessiner en grandeur réelle ce rectangle et sa diagonale [AC].

2. Calculer la mesure arrondie au degré de l’angle .

3. Démontrer que les angles et sont égaux.

4. La médiatrice du segment [AC] coupe la droite (AB) en E.

Placer le point E et montrer que le triangle ACE est isocèle.

5. En déduire une valeur approchée de la mesure de l’angle .

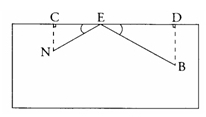
Exercice 17

L’unité de longueur est le centimètre.

Le rectangle ci-dessus représente une table de billard.

Deux boules de billard N et B sont placées telles que : CD = 90 ; NC = 25 ; BD = 35.

(Les angles sont droits.)

Un joueur veut toucher la boule N avec la boule B en suivant le trajet BEN, E étant entre C et D, et tel que la mesure de l’angle est égale à celle de .

. On pose ED = x.

l.

a. Donner un encadrement de x.

b. Exprimer CE en fonction de x.

2. Dans le triangle BED, exprimer en fonction de x.

3. Dans le triangle NEC, exprimer en fonction de x.

4.

a. En égalant les deux quotients trouvés aux questions 2. et 3.,

on trouve l’équation : 35(90 – x) = 25 x.

On ne demande pas de le justifier.

Résoudre cette équation.

b. En déduire la valeur commune des angles et arrondie au degré.

Exercice 18 : calculs de la mesure d’un angle
Calculer, pour chaque figure, la mesure de l’angle marqué (arrondir le résultat au degré près).

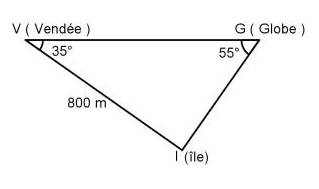
Exercice 19 : les voiliers Vendée
Les voiliers Vendée et Globe sont au large d’une île et vont la rejoindre pour y passer la nuit.
On peut schématiser leurs positions V et G comme figuré ci-contre.

Sachant que le voilier Vendée est à 800 m de l’île,  déterminer au mètre près la distance séparant Globe de l’île et la distance entre les deux voiliers.

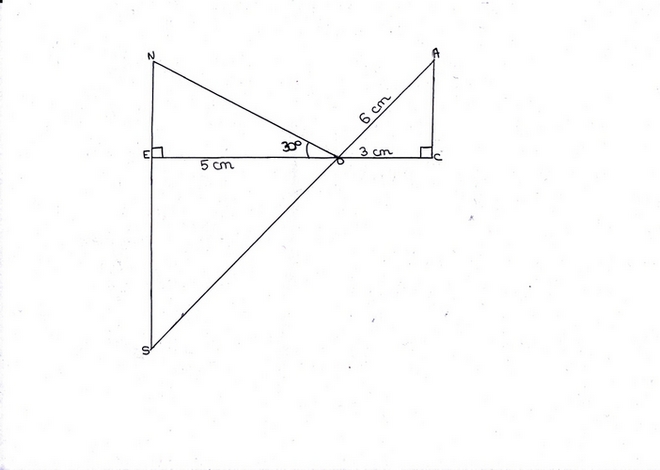
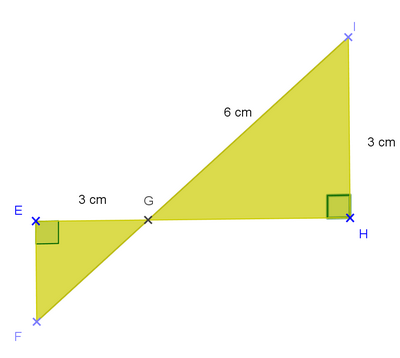
  Exercice 20 : triangles croisés
1. Calculer la mesure de .

2. En déduire la mesure de l’angle  .

3. Calculer les longueurs EF et FG arrondies au dixième .

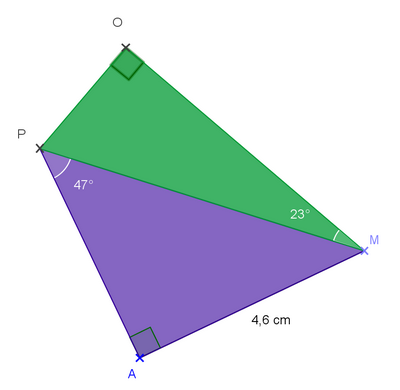
Exercice 21 : trigonométrie avec deux triangles
Calculer la longueur OM arrondie au millimètre .

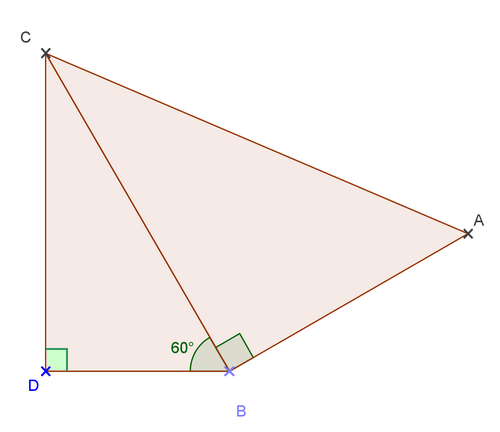
 Exercice 22 : trigonométrie dans le triangle rectangle
On donne BD = 4 cm , BA = 6 cm et .

1. Montrer que BC= 8 cm.

2. Calculer CD.

Donner la valeur arrondie au dixième.

3. Calculer AC.

4. Quelle est la valeur de  ?

5. En déduire la valeur arrondie au degré de  .

Exercice 23 :

1) Construire un triangle ABC rectangle en A sachant que :

AB = 6 cm et  = 35°.

2)  Calculer la longueur BC et la longueur AC ; on donnera les résultats au millimètre le plus proche.

Exercice 24 :

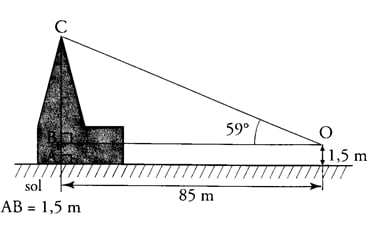
On veut mesurer la hauteur d’une cathédrale. Grâce à un instrument de mesure placé en O, à 1,5 m du sol et à 85 m de la cathédrale, on mesure l’angle  et on trouve 59°.

1) Déterminer la longueur CB au dixième de mètre le plus proche.

2) En déduire la hauteur de la cathédrale que l’on arrondira au mètre le plus proche.

Exercice 25 :

ABC est un triangle rectangle en A.

On donne AB = 5 cm et  = 35°.

1) Construire la figure en vraie grandeur.

2) Déterminer la longueur AC, arrondie au dixième de centimètre.

Exercice 26  :

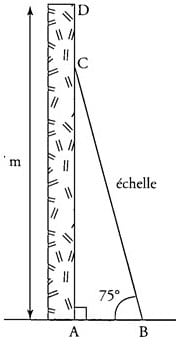
Une échelle de 6 mètres est appuyée contre un mur vertical de 7 mètres de haut. Par mesure de sécurité, on estime que l’angle que fait l’échelle avec le sol doit être de 75° (voir schéma ci-dessous).

l) Calculer la distance AB entre le pied de l’échelle et le mur. (On donnera le résultat arrondi au centimètre.)

2)  A quelle distance CD du sommet du mur se trouve le haut de l’échelle ? (On donnera le résultat arrondi au centimètre.)

Exercice 27 :

Tracer un cercle C de centre O et de rayon 4 cm. Tracer [AB], un diamètre de C.

Placer un point E sur le cercle C tel que :  = 40°.

1) Montrer que le triangle ABE est rectangle.

Calculer la valeur exacte de BE puis son arrondi au millimètre.

2) Placer le point D symétrique de B par rapport à E.

Démontrer que les droites (AD) et (OE) sont parallèles.

3) Quelle est la nature du triangle ABD ? Justifier.

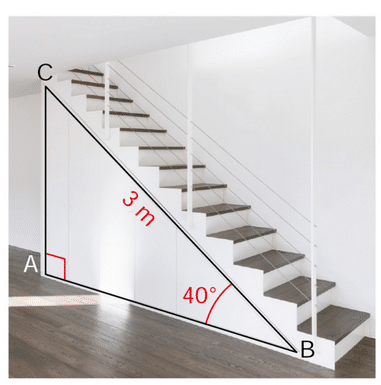
Exercice 28 :

Un câble de 20 m de long est tendu entre le sommet d’un poteau vertical et le sol horizontal. Il forme un angle de 40° avec le sol (voir schéma).

1. Calculer la hauteur du poteau.

2. Représenter la situation par une figure à l’échelle   (les données de la situation doivent être placées sur la figure).

Exercice 29 :

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

1) Dessiner en grandeur réelle ce rectangle et sa diagonale [AC].

2) Calculer la mesure arrondie au degré de l’angle  .

3) Démontrer que les angles   et    sont égaux.

4) La médiatrice du segment [AC] coupe la droite (AB) en E. Placer le point E et montrer que le triangle ACE est isocèle.

5) En déduire une valeur approchée de la mesure de l’angle .

Exercice 30 :

Pour propulser des billes, Mathieu a construit un plan incliné de 30° dont la

base mesure 15 cm de long.

Quelle est la longueur de la pente?

Donner l’arrondi au millimètre.

Exercice 31 :

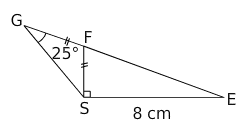
Sachant que les points E, F et G sont alignés, on veut calculer la longueur FS.

1.Calculer la mesure de l’angle .

2.Calculer la mesure de l’angle .

3.En déduire l’arrondi au dixième de FS.

Exercice 32 :

a. Utiliser les données de cette figure pour donner une valeur approchée au degré près de la
mesure de l’angle .

b.En déduire une valeur approchée de la mesure de l’angle .

Exercice 33 :

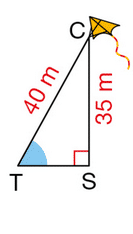
Tania fait voler son cerf-volant.
La ficelle a une longueur TC de 40 m.

Elle est tendue et le cerf-volant est à 35 m du sol.
Donner une valeur approchée au degré près de la mesure de l’angle .

Exercice 34 :

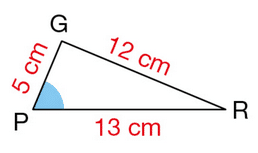
1. Pourquoi le triangle PGR ci-dessous est-il rectangle ?

2. Donner sous forme de fraction irréductible la valeur de:
a.    b.     c.

Exercice 35 :

1. Dans le triangle ABC rectangle en B, quel segment est :

a. l’hypoténuse ?

b. le côté adjacent à l’angle  ?
c. le côté opposé à l’angle ?
2. Dans le triangle BHC rectangle en H, quel angle a pour côté opposé :
a. [BH]? b. [CH]?

Exercice 36 :

Pour accéder à sa mezzanine, Lola doit installer un escalier.
Avec les données de cette figure, donner une valeur approchée au centième près de la longueur AB, en m.

Exercice 37 :

La tour du One World Trade Center a été inaugurée en 2014, à New York (États-Unis).

Une personne de 1,65 m, située à 100 m de la tour, mesure (O représente son œil).

Calculer une valeur approchée à l’unité près de la hauteur, en m, de cette tour.

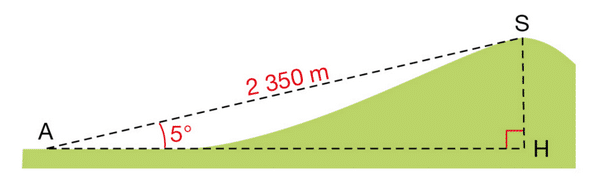
Exercice 38 :

Un géomètre, positionné en A, souhaite calculer l’altitude du sommet S d’une colline.

Son GPS lui indique qu’il se trouve lui-même à une altitude de 625 m.

Il effectue les mesures suivantes :

a. Donner une valeur approchée au centième près de la hauteur HS, en m, de la colline.
b. En déduire l’altitude du point S.

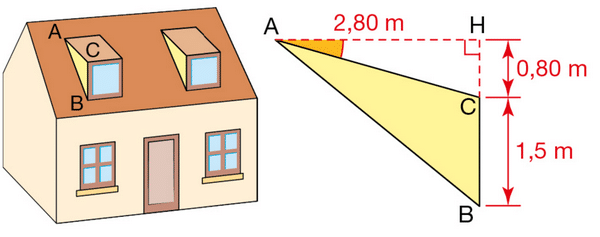
Exercice 39 :

Voici un plan de coupe de l’une des deux lucarnes de cette maison.

Déterminer une valeur approchée au degré près de :
a. la mesure de ,
b. la mesure de .

Exercice 40 :

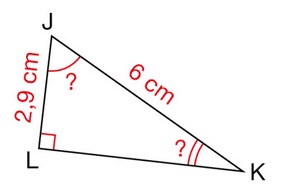
1) Construire un triangle IJK tel que :

JK = 8 cm ; IJ = 4,8 cm ; KI = 6,4 cm.

2) Démontrer que le triangle IJK est un triangle rectangle.

3) Calculer la mesure en degrés de l’angle  .

Donner la valeur arrondie au degré le plus proche.

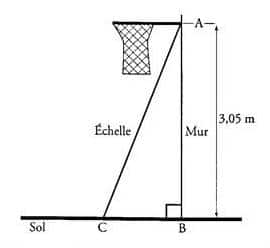
1. Paul veut installer chez lui un panier de basket. Il doit le fixer à 3,05 m du sol. L’échelle dont il se sert mesure 3,20 m de long.

À quelle distance du pied du mur doit-il placer l’échelle pour que son sommet soit juste au niveau du panier ? (Donner une valeur approchée au cm près.)

2. Calculer l’angle formé par l’échelle et le sol. (Donner une valeur approchée au degré près.)

Exercice 42 :

Soit ABC un triangle isocèle de base [BC], [AH] la hauteur issue du sommet A.

On a : BC = 8 cm et AH = 7 cm.

1) Construire le triangle ABC en justifiant la construction.

2) Calculer .

3) En déduire la valeur de l’angle   arrondie au degré près.

Exercice 43 :

La figure ci-dessous représente un triangle SET isocèle en E, et la hauteur [SH] issue de S. On ne demande pas de refaire la figure.

On sait que les segments [ES] et [ET] mesurent 12 cm et que l’aire du triangle SET est 42 cm².

1) Démontrer que la mesure h du segment [SH] est égale à 7 cm.

2) Calculer la valeur arrondie au millimètre près de la longueur EH.

3)  Calculer la mesure arrondie au degré près de l’angle .

Exercice 44 :

L’unité de longueur est le centimètre ; l’unité d’aire est le centimètre carré.

On considère la figure ci-contre :

• · le triangle ABC est rectangle en A ;
• · AB = 3,6 ;
• · BC = 6.

1) Calculer la mesure de l’angle  (on donnera l’arrondi au degré).

2) Calculer AC.

3) Calculer l’aire du triangle ABC.

4) Soit H le projeté orthogonal du point A sur la droite (BC).

Exprimer l’aire du triangle ABC en fonction de AH.

5) En déduire AH.

Exercice 45 :

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

1) Dessiner en grandeur réelle ce rectangle et sa diagonale [AC].

2) Calculer la mesure arrondie au degré de l’angle  .

3) Démontrer que les angles   et   sont égaux.

4) La médiatrice du segment [AC] coupe la droite (AB) en E. Placer le point E et montrer que le triangle ACE est isocèle.

5) En déduire une valeur approchée de la mesure de l’angle .