Statistiques : exercices de maths en 3ème corrigés en PDF.
Mis à jour le 13 décembre 2025
Exercice 1 – Problème de gymnastique
Dans une classe de 25 élèves, la moyenne d’EPS des filles, lors d’une évaluation de gymnastique est égale à 11 sur 20. La moyenne des garçons est égale à 9,5 sur 20. Sachant que la moyenne de la classe est égale à 10,4 sur 20, calculer le nombre de filles de la classe.
Exercice 2 – Exercice sur une hauteur
hauteur en (m) 1.2 1.3 1.4 1.5 1.6
Effectif 21 37 51 22 14
1. Calculer la moyenne de cette série .
2. Déterminer la médiane de cette série .
3. Interpréter les résultats obtenus précédemment .
Exercice 3 – Groupe de personnes
groupe de personnes
tailles en cm 130 145 155 160 170 175 180 190
effectifs 3 5 11 25 36 20 8 2
effectifs cumules
1) calculer la taille moyenne de ces personnes
2) Calculer le premier quartile Q1 ,la médiane et le troisième quartile Q3 de cette serie.
3) Calculer l’étendue de la série initiale des tailles ?
Exercice 4 – Etude d’un skieur
| 10<a<20< td= » »> | 20<a<30< td= » »> | 30<a<40< td= » »> | 40<a<50< td= » »> | 50<a<60< td= » »> | 60<a<70< td= » »> |
| 15 | .. | .. | .. | .. | .. |
| 240 | 628 | 556 | 370 | 356 | 190 |
1er colonne : Age noté « a »
2eme colonne : Centre des classe
3eme colonne : Effectifs
Pendant les vacances de Noël, Mr GLISSSE est parti skier à L’alpe d’Hurez .
Pendant une heure, on a relevé l’âge des personnes qui sont montées dans un télésiège ( voir le tableau)
1)Calculer le nombre de personnes ayant pris le télésiège pendant cette heure.
2)Compléter la 2eme ligne du tableau .
3)Calculer l’âge moyen des skieurs.
Arrondir le résultat à l’unité.
4) Calculer le pourcentage de skieurs ayant 50ans ou plus .Arrondir le résultat au dixième .
Exercice 5 – Note d’élèves
Voici les notes obtenues par 13 élèves à un devoir de mathématiques :
8;9;19;17;6;18;18;8;14;12;9;10;11
1. Calculer la moyenne arrondie au centième de cette série de notes.
2. Calculer le pourcentage d’élèves qui ont une note supérieure à cette moyenne de la classe.
3. Déterminer la médiane de cette série de notes.
4. Calculer le premier et le troisième quartile . Interprétez ces résultats.
5. Calculer l’étendue de la série.
Exercice 6 – Calculs statistiques
Cette série donne la répartition du pouls des élèves d’une classe après une course de 500 m.
Calculer la moyenne de cette série statistiques.
| Pouls | 65 | 72 | 75 | 80 | 82 | 90 |
| Effectif | 2 | 5 | 4 | 5 | 3 | 1 |
Exercice 7
Voici les distances en km des vingt et une étapes du Tour de France.
a. Calculer l’étendue de cette série.
b. Calculer la moyenne de cette série (arrondir au km).Interpréter ce résultat par une phrase.
c. Déterminer la médiane de cette série.
d. Les distances à parcourir pour les deux <<contre-la-montre>> individuels sont 29 km et 53 km.
Déterminer l’étendue, la moyenne, la médiane de la série dans ces deux <<contre-la-montre>>.
Exercice 8 – Problème de pourcentages
Au collège Michel Chasles, 200 élèves suivent avec beaucoup de sérieux les cours en classe de troisième.
Lors d’un brevet blanc, les notes obtenues par les élèves à l’épreuve commune de mathématiques sont scrupuleusement analysées.
Ces dernières sont regroupées dans le tableau ci-dessous.
| Notes | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Effectifs | 2 | 6 | 11 | 9 | 12 | 10 | 4 | 13 | 5 | 8 | 20 | 16 | 8 | 11 | 15 | 11 | 8 | 9 | 6 | 11 | 5 |
1. Calculer la moyenne des notes obtenues en mathématiques au brevet blanc par l’ensemble des élèves des classes de troisième.
2. Représenter cette série de résultats par un diagramme en bâtons.
3. A partir du tableau, donner les valeurs du premier et du troisième quartile de la série de notes.
4. A partir du tableau, donner la valeur de la médiane de la série de notes.
5. Quel est le pourcentage des élèves qui ont eu une note supérieure ou égale à 18.
Exercice 9 – Moyenne, médiane et quartiles
Un athlète du lancer de poids, participe à des épreuves éliminatoires en vue de son éventuelles sélection pour les championnats d’Europe.
Il est amené à réaliser 12 lancers dont les longueurs, en mètres, sont donnés ci-dessous.
1. Quelle est la moyenne de la série de lancers ? interpréter ce résultat par une phrase.
2. Quelle est la médiane de la série de lancers ?
3. Déterminer le premier quartile de la série de lancers ?
4. Déterminer le troisième quartile de la série de lancers ?
Exercice 10 – Problèmes sur les statistiques
Il y a deux correcteurs au brevet des collèges.
Le premier a 11 de moyenne avec 55 candidats et son collègue n’a que 9,5 de moyenne avec 45 candidats.
Quelle est la moyenne générale?
Exercice 11
Les gendarmes ont effectué un contrôle de vitesse sur le bord d’une route nationale.
| vitesse | [50;70[ | [70;90[ | [90;110[ | [110;130[ |
| effectif | 15 | 90 | 35 | 5 |
Calculer la vitesse moyenne des automobilistes contrôlés.
Exercice 12
La Polynésie française compte 219 500 habitants.
Leur répartition géographique est représentée par le diagramme circulaire suivant:
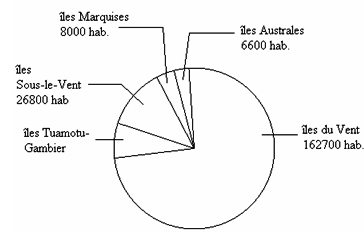
a. Calculer le nombre d’habitants des îles Tuamotu-Gambier
b. Calculer le pourcentage des habitants des îles Sous-le-Vent par rapport à la population totale.
Exercice 13
On a relevé la nationalité des vainqueurs des 85 premiers Tours de France cyclistes entre 1903 et 1998 .
La tableau ci-dessous donne le nombre de victoires par nationalité.
| France | Belgique | Italie | Espagne | Autres | |
| nombre de victoires | 36 | 18 | 9 | 9 | 13 |
| fréquence (en pourcent) |
1. Compléter le tableau.
2. Construire un diagramme circulaire représentant cette situation (on prendra 5 cm pour rayon du cercle).
On justifiera correctement le calcul des angles.
Exercice 14
Un devoir commun de mathématiques a été proposé à l’ensemble des classes de troisième d’un collège.
Les résultats sur 20 sont les suivants:
| 12 | 8 | 15 | 11 | 4 | 7 | 13 | 2 | 9 | 10 | 17 | 13 |
| 14 | 3 | 6 | 6 | 8 | 12 | 9 | 16 | 12 | 9 | 4 | 15 |
| 5 | 3 | 13 | 2 | 18 | 5 | 6 | 11 | 10 | 14 | 6 | 14 |
| 8 | 17 | 10 | 11 | 16 | 10 | 8 | 10 | 9 | 11 | 10 | 14 |
| 7 | 13 | 19 | 14 | 10 | 15 | 12 | 13 | 6 | 12 | 11 | 9 |
| 13 | 16 | 15 | 13 | 5 | 10 | 7 | 16 | 10 | 8 | 16 | 11 |
1. Recopier et compléter le tableau suivant:
| Note | 0 | 1 | ….. | 20 |
| Effectif | ||||
| fréquence | ||||
| effectif cumulé croissant | ||||
| fréquence cumulée croissante |
2. Répondre aux questions suivantes:
– combien d’élèves étaient présents au contrôle?
– combien d’élèves ont obtenu une note supérieure à 10?
– combien d’élèves ont obtenu une note inférieure à 12?
– quel est le pourcentage d’élèves ayant eu une note supérieure à 15?
– Quel est le pourcentage d’élèves ayant eu au plus 7?
3. Représenter la série par un diagramme en bâton
En déduire la médiane de ces notes.
4. Les professeurs de mathématiques emmènent en excursion les 36 élèves qui ont obtenu les meilleurs résultats.
Damien a eu 10. Partira-t-il en excursion?
5. Calculer la moyenne de cette série de notes.
Un élève est dit moyen s’il obtient une note strictement supérieure à 8 et inférieure à 12.
Calculer le pourcentage d’élèves moyens dans l’ensemble des classes de troisième.
Exercice 15 – Etude d’un tableau
Ce tableau donne la répartition des 29 495 000 logements en France selon leur catégorie.
| Catégorie | Fréquence (en %) |
| Résidence principales | 83,2 |
| Logements vacants | 6,8 |
| Logements occasionnels | 1 |
| Résidences secondaires | 9 |
1. Représenter cette distribution de fréquences par un diagramme circulaire .
2.Calculer le nombre de logements de chaque catégorie en arrondissant au millier .
Exercice 16 – Tirage du loto
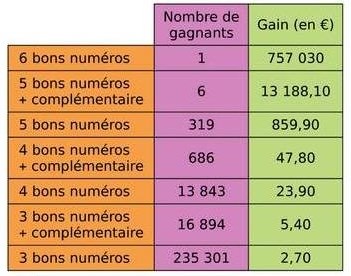
Le premier tirage du loto du mercredi 26 décembre a donné les résultats suivants.
a. A partir de ce tableau, déterminer le gain moyen d’un gagnant le 26 décembre.
b. Déterminer une médiane et les premier et troisième quartiles de la série des gains.
c. Quelle est l’étendue des gains?
Que devient cette étendue si on élimine 1 % des plus gros et des plus petits gagnants ?
d. Sachant que le loto consiste à tirer au sort six numéros distincts au hasard parmi 49 numéros.
Combien y a-t-il de grilles possibles?
Exercice 17 – Salaire des femmes et hommes dans une entreprise
Une entreprise emploie sept femmes et douze hommes.
Leurs salaires nets mensuels sont (en e) :
– Salaire des femmes : 1 090; 1 044; 3 470; 1 224; 1 250; 1 438; 1 072.
– salaire des hommes : 1 405; 1 070; 1 948;1 525;1 090;1 002;1 525;1 968; 1 224;2 096;1 703;1 126.
a. Calculer l’étendue de chacune des séries.
Comment pouvez-vous interpréter ces résultats ?
b. Calculer le salaire moyen pour chaque sexe (arrondir à l’euro si nécessaire).Comment pouvez-vous interpréter ces résultats ?
c. Déterminer une médiane des salaires pour chaque série.
Comment pouvez-vous interpréter ces résultats ?
d. Dans cette question, on considère la série composée des salaires de tous les employés de cette entreprise.
Calculer l’étendue et la moyenne, puis déterminer une médiane de cette série.
e. Reprendre les questions précédentes en ne tenant plus compte du salaire le plus élevé de chaque sexe.
Comparer les résultats obtenus.
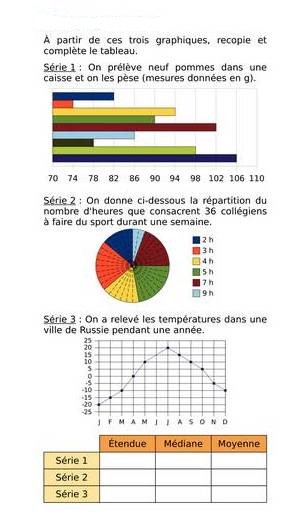
Exercice 18 – Etude de graphiques
Exercice 19 – Etendue, médiane et moyenne
A partir des trois tableaux de données, recopier et compléter le quatrième tableau.
Série 1 :
Nombre de personnes fréquentant un clb de remise en forme sur une semaine.
| Lu | Ma | Me | Je | Ve | Sa | Di |
| 32 | 38 | 21 | 49 | 60 | 84 | 24 |
Série 2 :
La pointure de 20 personnes.
| Pointure | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
| Effectif | 1 | 2 | 4 | 3 | 2 | 3 | 1 | 3 | 1 |
Série 3 :
Nous obtenons (sur 20) par une classe de troisième en français lors d’un contrôle.
| Notes | 4 | 5 | 7 | 8 | 9 | 12 | 13 | 15 | 17 | 18 |
| Effectif | 1 | 2 | 2 | 4 | 3 | 5 | 1 | 3 | 2 | 2 |
| Etendue | Médiane | Moyenne | |
| Série 1 | |||
| Série 2 | |||
| Série 3 |
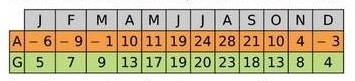
Exercice 20 – Climat et étude de températures
Ce tableau compare les températures mensuelles moyennes (en °C) au cours d’une année dans deux villes Alpha (A) et Gamma (G).
Pour chaque ville, répondre aux questions.
a. Calculer la température annuelle moyenne.
b. Déterminer une température médiane.
c. Calculer l’étendue des températures.
d. Décrire le climat.
Exercice 21 – Quartiles et statistiques
notes 6 7 9 10 11 12 14 15 16 19
effectifs 3 4 4 2 1 3 2 4 1 2
1) Calculer la fréquence des élèves de la classe qui ont eu une note supérieur ou égale à la moyenne. Le résultat sera arrondi au centième près
2) Déterminer la note médiane
3a) Déterminer Q1 et Q3, les valeurs du premier et troisième quartiles de la série
3b) Calculer le pourcentage d’élèves ayant une note inférieure ou égal a Q3.
Le résultat sera arrondi au dixième .
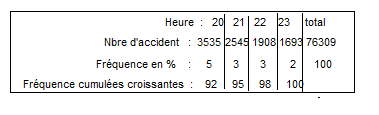
Exercice 22 – Etude des accidents de la route
Une personne affirme que 25% des accidents se produisent entre 20h et 24h. Cette affirmation est t elle vraie ? Justifier la réponse. (4581 accidents se sont produits entre 8h et 9h) Les nombres de 20 à 23h ( il n’y a pas 24h dans le tableau) :
Exercice 23 – Problème de températures
» Voici les températures moyennes mensuelles de deux villes, en degrés Celsius :
MEXICO
J F M A M J
12,4 14,1 16,2 17,4 18,4 17,7
J A S O N D
16,7 16,8 16,3 15,1 13,9 12
BARCELONE
J F M A M J
9,5 10,3 12,4 14,6 17,7 21,5
J A S O N D
24,3 24,3 21,8 17,6 13,5 10,3
1- Pour chacune de ces villes:
a- calculer l’ étendue de la série des températures ;
b- estimer la température moyenne annuelle ;
c- déterminer la médiane de la série.
2- Quels calculs permettent d’affirmer :
a- » Il fait plus chaud à Barcelone qu’a Mexico » ?
b- » Les écarts de températures sont moindres à Mexico » ?
c- » Dans ces deux villes, la température est supérieure à 16°C la moitié au moins de l’année. » ?
Exercice 24 – Etude d’une entreprise
Cher l’entreprise HITI
Salaire moyen en francs des hommes : 168000
Salaire moyen en francs des femme : 120000
Effectif hommes : 50
Effectif femme : 50
Cher l’entreprise KALU Salaire moyen en francs des hommes : 180000
Salaire moyen en francs des femme : 132000
Effectif hommes : 20
Effectif femme : 80
Kevin dit a sa soeur » en moyenne, on est mieux payé chez KALU » Qu’en pensez vous ?
Exercice 25 :
Taraina dirige une école de danse pour adolescents.
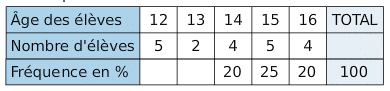
Elle a relevé dans un tableau l’âge de ses élèves, ainsi que la fréquence des âges.
- Compléter le tableau suivant :
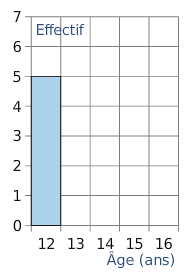
2. Ci-dessous, compléter le diagramme en barre des effectifs.
- Quelle est, dans cette école, la fréquence des élèves ayant 14 ans ?
- Quelles sont l’étendue et la médiane de cette série statistiques ?
Exercice 26 :
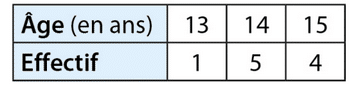
Voici la répartition des âges des élèves d’une école de cirque.
1. Quelle est la fréquence des élèves ayant 14 ans ?
2. a. Pour pouvoir participer à un festival, le groupe doit avoir un âge moyen inférieur ou égal à 14 ans.
Est-ce le cas ?
b. Le responsable a la possibilité d’accepter un nouvel élève, soit de 11 ans, soit de 16 ans.
Lequel va-t-il choisir ? Pourquoi ?
c. Le groupe peut-il alors participer au festival ?
Exercice 27 :
Voici un résumé des salaires nets mensuels, en euros, des salariés d’une grande entreprise.
Pour chaque affirmation, dire si elle est vraie ou fausse.
a. La moitié des salariés gagnent plus de 2 297 € par mois.
b. Si l’on ne prend pas en compte le salaire du PDG, le salaire moyen reste le même.
c. Si l’on ne prend pas en compte les salaires du PDG et de la personne qui a le plus bas salaire, le
salaire médian reste le même.
Exercice 28 :
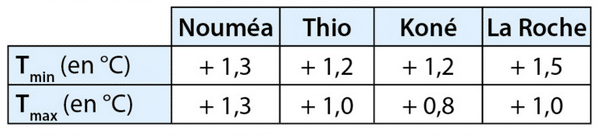
Le tableau ci-dessous présente l’évolution des températures minimales et maximales
observées en différents lieux de Nouvelle-Calédonie au cours des 40 dernières années.
a. Ce tableau traduit-il une augmentation ou une diminution des températures ? Expliquer.
b. En quel lieu la température minimale a-t-elle le plus augmenté ?
c. Calculer l’augmentation moyenne des températures minimales et celle des températures
maximales depuis 40 ans.
Exercice 29 :
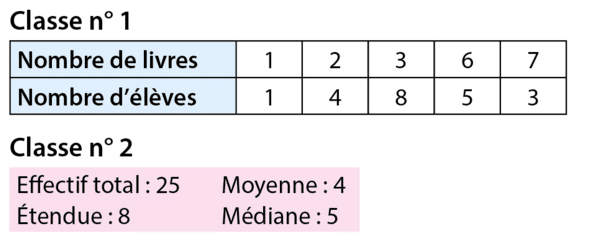
Deux classes d’un collège ont répondu à la question suivante : « Combien de livres avez-vous
empruntés au CDI durant les 12 derniers mois ? ».
Les deux classes ont communiqué leurs réponses de deux façons différentes.
a. Comparer les nombres moyens de livres empruntés dans chaque classe.
b. Un « grand lecteur » est un élève qui a emprunté 5 livres ou plus.
Quelle classe a le plus de « grands lecteurs » ?
c. Dans quelle classe se trouve l’élève ayant emprunté le plus de livres ? Expliquer.
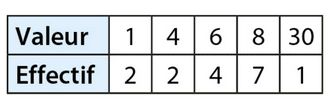
Exercice 30 :
a. Calculer mentalement la moyenne de cette série.
b. La valeur 30 de cette série est exceptionnelle.
Calculer mentalement la moyenne de la série privée de la valeur 30.
Exercice 31 :
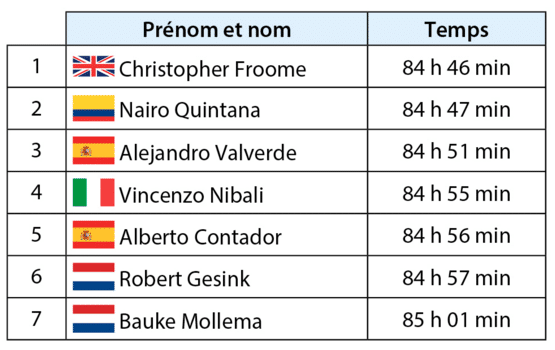
Voici le classement général des sept premiers coureurs à l’issue de la 21° étape du tour de France
2015.
1. Calculer la différence entre les temps de course de Bauke Mollema et de Christopher Froome.
2. On considère la série statistique des temps de course.
a. Que représente pour la série statistique la différence calculée à la question 1 ?
b. Quelle est la médiane de cette série ?
Exercice 32 :
Cette série statistique représente les salaires (en €) de 15 personnes.
1 200 ; 900 ; 1 100 ; 1 150 ; 2 300 ; 1 640 ; 1 500 ; 2 065 ; 1 700 ; 1 370 ; 990 ; 2 650 ; 1 230 ; 3 100 ; 850
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
Exercice 33 :
Cette série statistique représente les tailles (en m) de 17 personnes.
1,75 ; 1,68 ; 1,76 ; 1,89 ; 1,83 ; 1,91 ; 1,78 ; 1,79 ; 1,74 ; 1,67 ; 1,74 ; 1,80 ; 1,75 ; 1,85 ; 1,87 ; 1,73 ; 1,90
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
Exercice 34 :
Cette série statistique représente les poids (en kg) de 23 personnes.
75 ; 57 ; 87 ; 95 ; 73 ; 76 ; 78 ; 80 ; 75 ; 75 ; 64 ; 61 ; 101 ; 91 ; 79 ; 87 ; 84 ; 76 ; 65 ; 63 ; 98 ; 59 ; 81
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
Exercice 35 :
Cette série statistique représente les notes (sur 20) de 22 élèves.
7,5 ; 13 ; 14,5 ; 19,5 ; 12 ; 14 ; 10,5 ; 5 ; 4 ; 9,5 ; 17 ; 15,5 ; 18 ; 7 ; 8,5 ; 20 ; 11 ; 11,5 ; 11 ; 10 ; 12 ; 13,5
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
Exercice 36 :
Cette série statistique représente les âges de 24 élèves.
14 ; 14 ; 14 ; 13 ; 14 ; 15 ; 15 ; 14 ; 16 ; 17 ; 15 ; 14 ; 13 ; 14 ; 14 ; 13 ; 13 ; 15 ; 14 ; 16 ; 15 ; 14 ; 13 ; 15
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
Exercice 37 :
Cette série statistique représente les températures moyennes au mois de mai (en °C) dans 24 grandes villes.
14 ; 13 ; 16 ; 22 ; 11 ; 17 ; 16 ; 18 ; 23 ; 24 ; 18 ; 9 ; 20 ; 12 ; 17 ; 10 ; 18 ; 7 ; 21 ; 9 ; 10 ; 17 ; 19 ; 9
1. Classer ces valeurs dans l’ordre croissant :
2. Déterminer la moyenne, l’étendue et la médiane de cette série statistique.
|
Moyenne = |
Étendue = |
Médiane = |
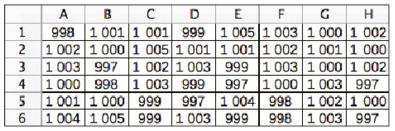
modèle si les lots de conducteurs ohmiques dont ils disposent ont
bien une résistance de 1 000
b. Déterminer à l’aide du tableur la moyenne, la médiane et l’étendue des mesures.
2. Les résultats d’un autre groupe d’élèves figurent dans cette feuille de calcul.

b. Déterminer la moyenne, la médiane et l’étendue des mesures.
c. Comparer ces deux séries de mesures.
Que peut-on remarquer ?
Quelle Série est la moins dispersée ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «statistiques : exercices de maths en 3ème corrigés en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.