Théorème de Thalès : cours en maths en 3ème en PDF à imprimer.

Sommaire de cette fiche

1 0. Un peu d’histoire :
2 I. Produit en croix :
3 II. Théorème de Thalès (partie directe) :
- 3.1 1. Les trois configurations de Thalès :
- 3.2 2. Enoncé du Théorème de Thalès :
4 III. Réciproque du Théorème de Thalès :
- 4.1 1.Théorème (partie réciproque) :

Le théorème de Thalès dans un cours de maths en 3ème faisant intervenir la partie directe et réciproque ainsi que la notion de proportionnalité et les égalités des rapports ainsi que la règle du produit en croix en classe de troisième.

0. Un peu d’histoire :

Point de vue historique :

Thalès était un savant grec qui vécut entre -627 et -547.Originaire de la ville de Milet, il était un généraliste des sciences comme la majorité de ses confrères de l’époque.

La propriété, que l’on va étudier, va nous montrer la corrélation entre la proportionnalité des longueurs et le parallélisme.

Cette propriété est connue et employée depuis l’antiquité.

Le théorème de Thalès ne serait pas dû à la personne dont il porte le nom.

Ce sont en fait des français qui le baptisèrent ainsi à la fin du XIXème siècle.

I. Produit en croix :

Afin de pouvoir étudier le théorème de Thalès convenablement, il est impératif de bien maîtriser le produit en croix ( ou règle de trois). On utilise le produit en croix pour résoudre des équations du style : $\frac{x}{3}=\frac{5}{6}$ .

On obtient $6\,\times \,x\,=\,5\times \,3$ puis

$\frac{6\times \,x}{6\,}=\frac{5\times \,3\,}{6}$ soit $x=\frac{5}{2}$

Exemples : résoudre les équations.

$a.\frac{7x}{5}=\frac{7}{10}$

$b.\frac{3}{x}=\frac{6}{17}$

$c.\frac{4}{5}=\frac{2}{x}$

$d.\frac{9}{4}=\frac{x}{3}$

II. Théorème de Thalès (partie directe) :

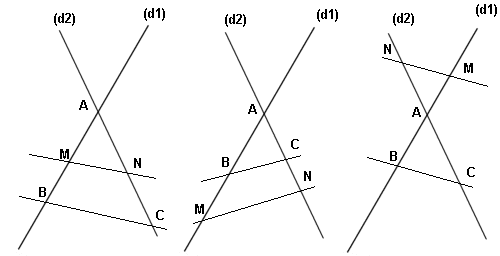
1. Les trois configurations de Thalès :

2. Enoncé du Théorème de Thalès :

Propriété : partie directe :

Soient ABC et AMN deux triangles.

Si $M\in(AB)\,;\,N\in(AC)\,;\,(MN)//(BC)$

Alors d’après la partie directe du théorème de Thalès, nous avons :

$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ .

Remarque :

La partie directe du théorème de Thalès , nous permet de calculer une longueur si des droites sont parallèles.

III. Réciproque du Théorème de Thalès :

1.Théorème (partie réciproque) :

Propriété : partie réciproque :

Si ABC sont deux triangles tels que A, M, B et A, N, C sont alignés dans le même ordreet $\frac{AM}{AB}=\frac{AN}{AC}$

Alors d’après la partie réciproque du théorème de Thalès, les droites (MN) et (BC) sont parallèles.

Exemple :

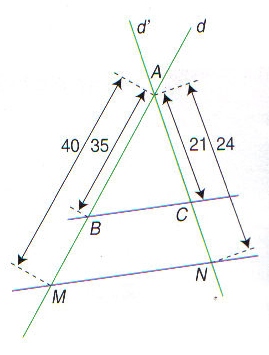
On donne la figure ci-dessous:

AB= 35 m; AM=40 m; AC=21m; AN=24m.

On sait que les points A,B,M et A,C,N sont dans le même ordre.

Par ailleurs :

$\frac{AM}{AB}=\frac{40}{35}=\frac{8}{7}$ et $\frac{AN}{AC}=\frac{24}{21}=\frac{8}{7}$

donc $\frac{AM}{AB}=\frac{AN}{AC}$ .

D’après la partie réciproque du théorème de Thalès, On peut donc en conclure que les droites (BC) et (MN) sont parallèles.

Remarques :

La partie réciproque du théorème de Thalès, nous permet de vérifier si des droites sont parallèles.- Quand les rapports ne sont pas égaux, on conclut que les droites ne sont pas parallèles d’après la partie contraposée du théorème de Thalès.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «théorème de Thalès : cours de maths en 3ème en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 152 cours et exercices de maths téléchargés en PDF.