DIPLOME NATIONAL DU BREVET
SESSION 2021
MATHEMATIQUES
Centres étrangers
Exercice 1 : (24 points)
Dans cet exercice, chaque question est indépendante. Aucune justification n’est demandée.
1) Décomposer 360 en produit de facteurs premiers.
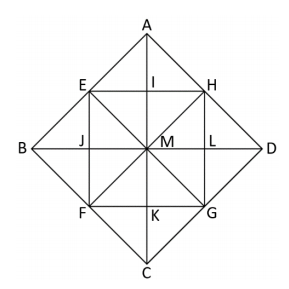
2) A partir du triangle BEJ, rectangle isocèle en J, on a obtenu par pavage la figure ci-dessous.
a) Quelle est l’image du triangle BEJ par la symétrie d’axe (BD) ?
b) Quelle est l’image du triangle AMH par la translation qui transforme le point E en B ?
c) Par quelle transformation passe-t-on du triangle AIH au triangle AMD ?
3) Calculer en détaillant les étapes :
On donnera le résultat sous la forme d’une fraction irréductible.
4) Pour cette question, on indiquera sur la copie l’unique bonne réponse.
Sachant que le diamètre de la Lune est d’environ 3 474 km, la valeur qui approche le mieux son
volume est :
5) On considère un triangle RST rectangle en S.
Compléter le tableau donné en ANNEXE à rendre avec la copie.
On arrondira la valeur des angles l’unité.
Exercice 2 : (21 points)
Partie 1
Dans cette première partie, on lance un dé bien équilibré six faces numérotées de 1 à 6,
puis on note le numéro de la face du dessus.
1) Donner sans justification les issues possibles.
2) Quelle est la probabilité de l’événement A : « On obtient2 » ?
3) Quelle est la probabilité de l’événement B : « On obtient un nombre impair » ?
Partie 2
Dans cette deuxième partie, on lance simultanément deux dés bien équilibrés six faces, un
rouge et un vert.
On appelle « score » la somme des numéros obtenus sur chaque dé.
1) Quelle est la probabilité de l’événement C: « le score est 13 » ? Comment appelle-t-on
un tel événement ?
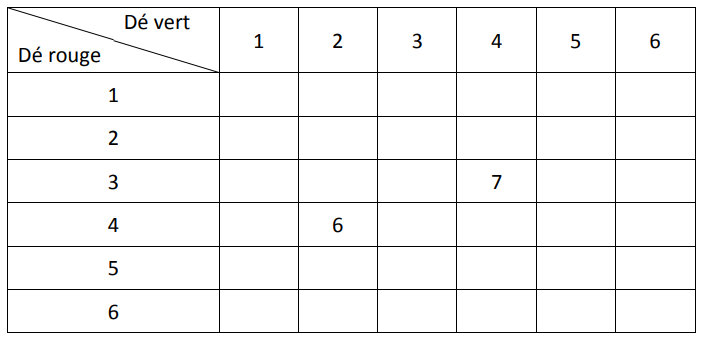
2) Dans le tableau double entrée donné en ANNEXE, on remplit chaque case avec la
somme des numéros obtenus sur chaque dé.
a) Compléter, sans justifier, le tableau donné en ANNEXE rendre avec la copie.
b) Donner la liste des scores possibles.
3)
a) Déterminer la probabilité de l’événement D : « le score est 10 ».
b) Déterminer la probabilité de l’événement E : « le score est un multiple de 4 ».
c) Démontrer que le score obtenu a autant de chance d’être un nombre premier qu’un
nombre strictement plus grand que 7.
Exercice 3 : (16 points)
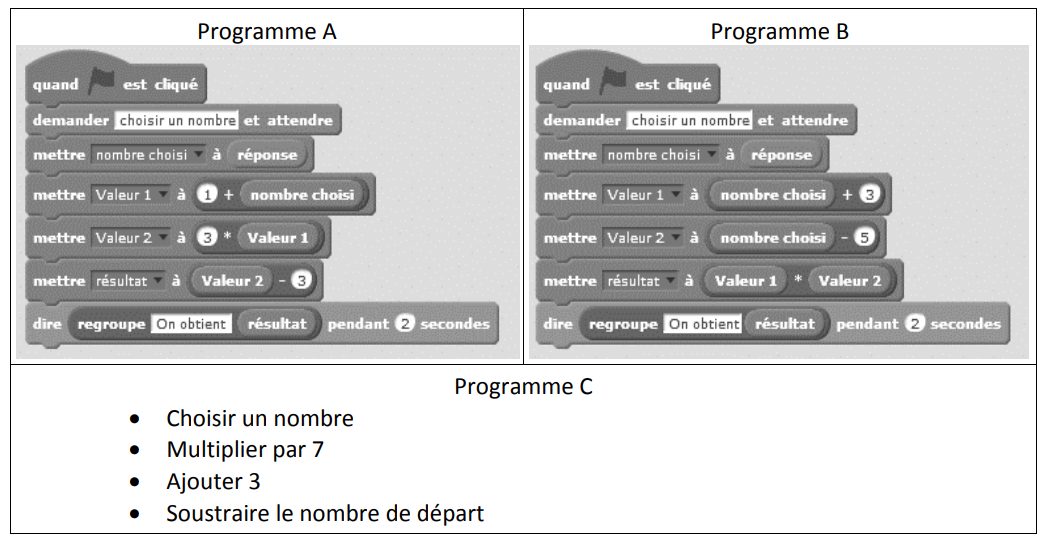
Un professeur propose à ses élèves trois programmes de calculs, dont deux sont réalisés
avec un logiciel de programmation.
1)
a) Montrer que si on choisit 1 comme nombre de départ alors le programme A affiche
pendant 2 secondes « On obtient 3 ».
b) Montrer que si on choisit 2 comme nombre de départ alors le programme B affiche
pendant 2 secondes « On obtient —15 ».
2) Soit x le nombre de départ, quelle expression littérale obtient-on la fin de l’exécution
du programme C ?
3) un élève affirme qu’avec un des trois programmes on obtient toujours le triple du
nombre choisi. A-t-il raison ?
4)
a) Résoudre l’équation (x + 3)(x — 5) = O.
b) Pour quelles valeurs de départ le programme B affiche-t-il « On obtient O » ?
5) Pour quelle(s) valeur(s) de départ le programme C affiche-t-il le même résultat que le
programme A ?
Exercice 4 : (19 points)
Aurélie fait du vélo en Angleterre au col de Hardknott.
Elle est partie d’une altitude de 251 mètres et arrivera au sommet une altitude de 393
mètres.
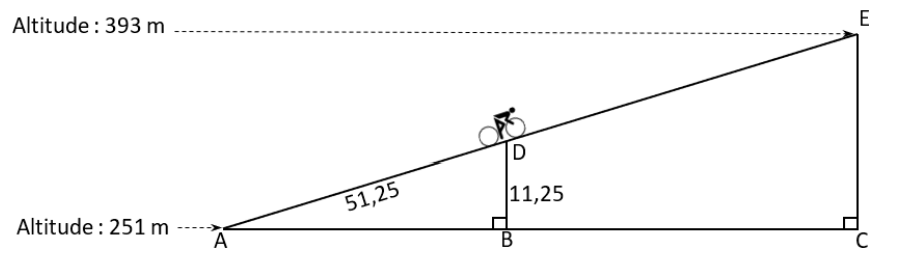
Sur le schéma ci-dessous, qui n’est pas en vraie grandeur, le point de départ est représenté
par le point A et le sommet par le point E. Aurélie est actuellement au point D.
Les droites (AB) et (DB) sont perpendiculaires.
Les droites (AC) et (CE) sont perpendiculaires.
Les points A, D et E sont alignés. Les points A, B et C sont alignés.
AD = 51,25 m et DB = 11,25 m.
1) Justifier que le dénivelé qu’Aurélie aura parcouru, c’est-à-dire la hauteur EC, est égal à
142 m.
2)
a) Prouver que les droites (DB) et (EC) sont parallèles.
b) Montrer que la distance qu’Aurélie doit encore parcourir, c’est-à-dire la longueur DE,
est d’environ 596 m.
3) On utilisera pour la longueur DE la valeur 596 m.
Sachant qu’Aurélie roule une vitesse moyenne de 8 km/h, si elle part 9h55 du
point D, quelle heure arrivera-t-elle au point E ? Arrondir la minute.
Exercice 5 : (20 points)
Une station de ski propose ses clients trois formules pour la saison d’hiver :
- Formule A : on paie 36,50€ par journée de ski.
- Formule B : on paie 90 € pour un abonnement « SkiPlus » pour la saison, puis 18,50 €
par journée de ski. - Formule C : on paie 448,50 € pour un abonnement « SkiTotal » qui permet ensuite un
accès gratuit la station pendant toute la saison.
1) Marin se demande quelle formule choisir cet hiver.
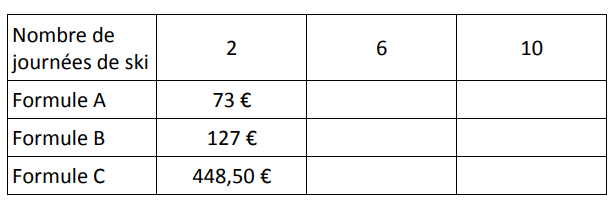
II réalise un tableau pour calculer le montant payer pour chacune des formules en fonction du nombre de journées de ski.
Compléter, sans justifier, le tableau fourni en ANNEXE rendre avec la copie.
2) Dans cette question, x désigne le nombre de journées de ski.
On considère les trois fonctions f, g et h définies par :
a) Laquelle de ces trois fonctions représente une situation de proportionnalité ?
b) Associer, sans justifier, chacune de ces fonctions la formule A, B ou C correspondante.
c) Calculer le nombre de journées de ski pour lequel le montant payer avec les formules A et B est identique.
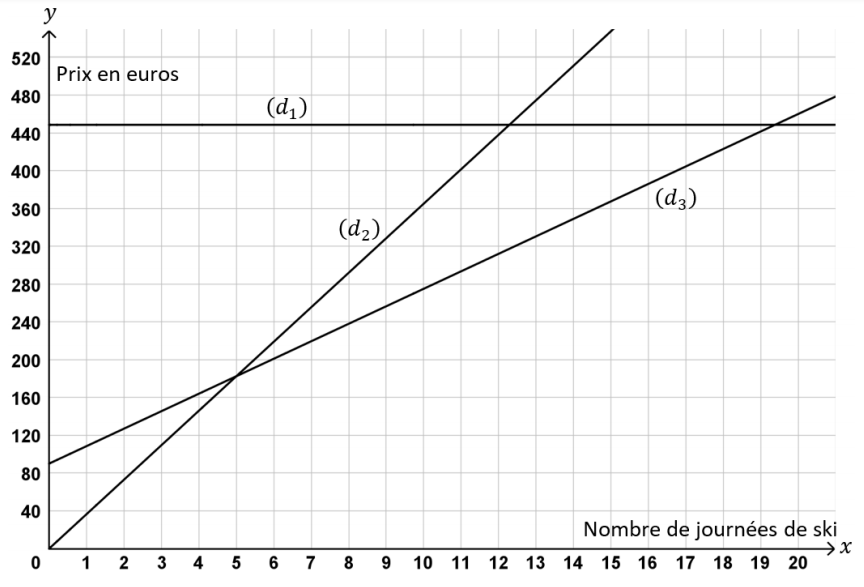
3) On a représenté graphiquement les trois fonctions dans le graphique ci-dessous.
Sans justifier et l’aide du graphique :
a) Associer chaque représentation graphique (d1), (d2) et (d3) la fonction f, g ou h correspondante.
b) Déterminer le nombre maximum de journées pendant lesquelles Marin peut skier
avec un budget de 320 € , en choisissant la formule la plus avantageuse.
c) Déterminer à partir de combien de journées de ski il devient avantageux de choisir la
formule C.
ANNEXE rendre avec la copie.
Exercice 1 question 5) :
Exercice 2 Partie 2 question 2) a) :
Exercice 5 question 1) :
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2021 et centres étrangers : sujet et corrigé du brevet.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
