Trigonométrie dans le triangle rectangle : cours de maths en 3ème en PDF.

Mis à jour le 16 avril 2025

Sommaire

🧮Cours de Mathématiques

3ème • Collège

Trigonométrie dans le triangle rectangle

📖 Temps de lecture : 5 min

🎯 Niveau : Collège

📱 Format : Gratuit

📄 PDF : Disponible

La trigonométrie dans le triangle rectangle dans un cours de maths en 3ème faisant intervenir le cosinus (cos), le sinus (sin) et la tangente (tan) d’un angle aigü ainsi que le calcul de la mesure d’un angle à l’aide de la calculatrice. Dans cette leçon en troisième, nous veillerons à mettre la calculatrice en mode degré (DEG).

0. Introduction :un peu d’histoire

Point de vue historique :

Le mot vient du grec « trigone » (triangle) et « metron » (mesure).Dans l‘Encyclopédie (1751), Jean le Rond d‘Alembert (1717 ; 1783) définit la trigonométrie comme :

« l‘art de trouver les parties inconnues d‘un triangle par le moyen de celles qu‘on connaît ».

C‘est bien la démarche qui est demandée aux élèves du collège.

I. Relations trigonométriques dans le triangle rectangle :

Théorème :

Dans un triangle rectangle ABC, on peut définir les relations suivantes entre les angles aigus et les différentes longueurs des côtés.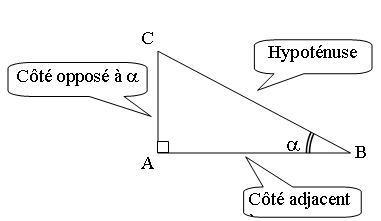

Définition :

– Le cosinus d’un angle aigu est donné par:

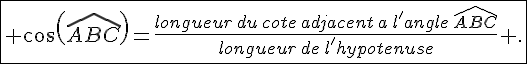
$\fbox{ cos(\widehat{ABC})=\frac{longueur\,du\,cote\,adjacent\,a\,l'angle\,\widehat{ABC}}{longueur\,de\,l'hypotenuse} .$

– Le sinus d’un angle aigu est donné par :

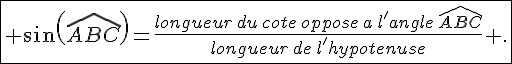
$\fbox{ sin(\widehat{ABC})=\frac{longueur\,du\,cote\,oppose\,a\,l'angle\,\widehat{ABC}}{longueur\,de\,l'hypotenuse} .$

– La tangente d’un angle aigu est donnée par :

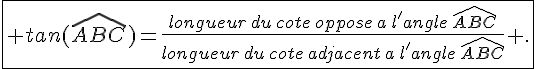
$\fbox{ tan(\widehat{ABC})=\frac{longueur\,du\,cote\,oppose\,a\,l'angle\,\widehat{ABC}}{longueur\,du\,cote\,adjacent\,a\,l'angle\,\widehat{ABC}} .$

Moyen mnémotechnique :

SOH-CAH-TOA

Explications:

CAH: Cos(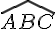 $\widehat{ABC}$ )= (longueur du cote Adjacent a l’angle 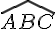$\widehat{ABC}$ ) : (longueur de l’Hypotenuse )

SOH: Sin(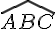 $\widehat{ABC}$ )= (longueur du cote Opposé a l’angle 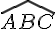$\widehat{ABC}$ ) : (longueur de l’Hypotenuse )

TOA: Tan(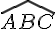 $\widehat{ABC}$ )= (longueur du cote Opposé a l’angle 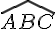$\widehat{ABC}$ ): (longueur du cote Adjacent a l’angle $\widehat{ABC}$ )

Remarques :

– Le sinus et le cosinus d‘un angle sont toujours compris entre – 1 et 1.

– Par contre, la tangente d‘un angle aigu peut prendre toutes les valeurs.

Exemples :

Si AC=16 cm et BC=20 cm, calculer 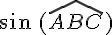$sin\,(\widehat{ABC})$ .

[ Réponse : 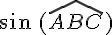$sin\,(\widehat{ABC})$ =0,8]

Si AC=16 cm et AB= 12 cm, calculer 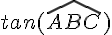$tan(\widehat{ABC})$

[ Réponse : 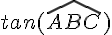$tan(\widehat{ABC})$ =1,33]

II. Détermination de la mesure d’un angle en degré, connaissant son cox ou sin x ou tan x :

Méthodologie :

La détermination de la mesure d‘un angle connaissant son cos x, sin x ou tan x s‘effectue à l‘aide de la calculatrice en utilisant les touches :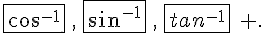 $\fbox{cos^{-1}}\,,\,\fbox{sin^{-1}}\,,\,\fbox{tan^{-1}}\,\, .$

En ayant vérifié, préalablement, que la calculatrice est en mode degré 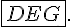$\fbox{DEG}.$

Exemples :

Si cos x = 0,5 alors $x=cos^{-1}(0,5)=60^o .$

Si sin x = 0,5 alors 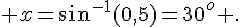$x=sin^{-1}(0,5)=30^o .$

Si tan x = 1 alors 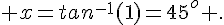$x=tan^{-1}(1)=45^o .$

III. Formules Trigonométriques :

Propriété :

Pour tout angle x, les égalités suivantes sont toujours vraies :

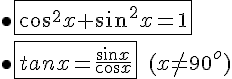
$\bullet \fbox{cos^2 x+sin^2 x = 1} \\ \\ \bullet \fbox{tanx=\frac{sin x}{cos x}}\,\,\,(x\neq 90^o)$

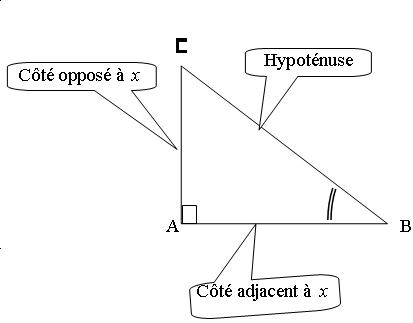
Preuve :

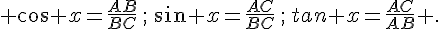
$cos x=\frac{AB}{BC}\,;\,sin x=\frac{AC}{BC}\,;\,tan x=\frac{AC}{AB} .$

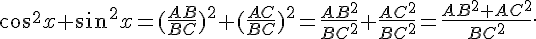
$cos^2 x + sin^2 x =(\frac{AB}{BC})^2+(\frac{AC}{BC})^2=\frac{AB^2}{BC^2}+\frac{AC^2}{BC^2}=\frac{AB^2+AC^2}{BC^2} .$

Or ABC est rectangle en A, donc d‘après la partie directe du théorème de Pythagore : AB²+AC²=BC²

D’où :

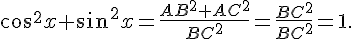
$cos^2 x + sin^2 x =\frac{AB^2+AC^2}{BC^2}=\frac{BC^2}{BC^2}=1 .$

Puis

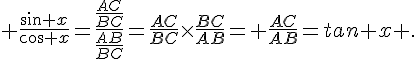
$\frac{sin x}{cos x}=\frac{\frac{AC}{BC}}{\frac{AB}{BC}}=\frac{AC}{BC}\times \frac{BC}{AB}= \frac{AC}{AB}=tan x .$

4.3/5 - (28467 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «trigonométrie dans le triangle rectangle : cours de maths en 3ème en PDF.» au format PDF.

Ressources de troisième

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Trigonométrie dans le triangle rectangle : cours de maths en 3ème en PDF.

0. Introduction :un peu d’histoire

I. Relations trigonométriques dans le triangle rectangle :

II. Détermination de la mesure d’un angle en degré, connaissant son cox ou sin x ou tan x :

III. Formules Trigonométriques :

Vous avez assimilé le cours sur la trigonométrie en 3ème ?

Résumé-Quiz

Information

Résultats

Categories

Ressources de troisième

Cours de troisième

Exercices de troisième

Brevet

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques

Score moyen
Votre score