DIPLÔME NATIONAL DU BREVET
SESSION 2024
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points
Exercice 1 (20 points)
On considère la figure ci-dessous dans laquelle :
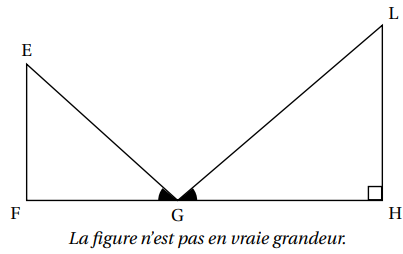
• Les points F, G et H sont alignés
• (LH) est perpendiculaire à (FH)
• EF = 18 cm; FG = 24 cm; EG = 30 cm;
GH = 38,4 cm
• 
.
1. Montrer que le triangle EFG est rectangle en F.
2. Calculer la mesure de l’angle .
Donner l’arrondi au degré près.
3. Montrer que les triangles EGF et LGH sont semblables.
4. Parmi les propositions suivantes, quel est le coefficient d’agrandissement qui permet
de passer du triangle EFG au triangle LHG ?
Expliquer.
5. Quel est le périmètre du triangle LGH ?
Exercice 2 (21 points)
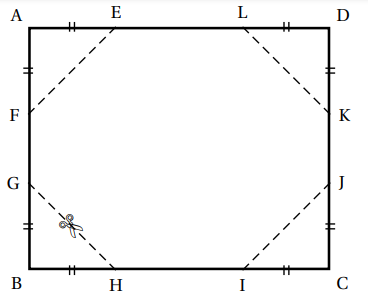
À partir d’une feuille rectangulaire de dimension 10 cm sur 8 cm, on coupe les quatre coins de manière identique.
On obtient ainsi un polygone FELKJIHG et quatre triangles rectangles isocèles égaux comme représenté ci-dessous.
AD = 10 cm; AB = 8 cm.
Les deux parties sont indépendantes.
Première partie : on suppose que AE = 3 cm.
Brevet des collèges A. P. M. E. P.
1. Quelle est l’aire du triangle AEF ?
2. En déduire l’aire du polygone FELKJIHG.
Deuxième partie :
On souhaite que l’aire du polygone FELKJIHG soit de 60 cm².
Pour cela, on fait varier la longueur AE et on observe l’effet sur l’aire du polygone FELKJIHG.
On note x la longueur AE exprimée en cm.
3. a. Exprimer l’aire du triangle AEF en fonction de x.
b. Montrer que l’aire du polygone FELKJIHG, en cm², est donnée par l’expression 80−2x².
4. On considère la fonction
À l’aide d’un tableur, on a produit le tableau de valeurs ci-dessous :
Proposer une formule qui a pu être saisie en B2 avant d’être étirée vers la droite.
Ne pas justifier.
5. Voici la courbe représentative de la fonction f :
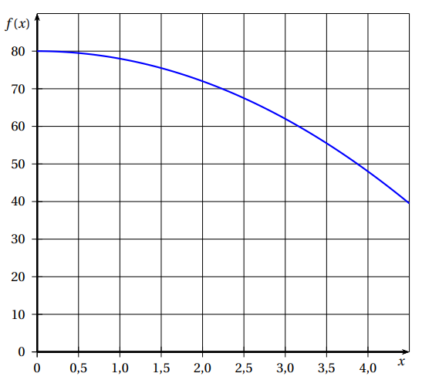
a. La fonction f est-elle affine ?
b. Par lecture graphique, déterminer une valeur approchée de la longueur AE permettant d’obtenir un polygone FELKJIHG d’aire égale à 60 cm².
c. Trouver par le calcul la valeur exacte de cette longueur.
Exercice 3 (20 points)
Pour chacune des affirmations, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. On considère le tableau ci-dessous :
Affirmation 1 : « Le prix est proportionnel au nombre de baguettes. »
2. On considère ci-dessous le point A sur une droite graduée :
Affirmation 2 : « L’abscisse du point A est un nombre décimal. »
3.
On considère cet engrenage qui est composé d’une roue A à 8 dents et d’une roue B à 12 dents.
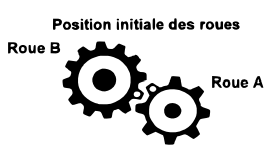
Affirmation 3 : « Cet engrenage sera dans la même position au bout de 6 tours pour la roue A et de 4 tours pour la roue B. »
4. Affirmation 4 :
« Pour tout nombre x, l’égalité suivante est vraie : (x +8)(2x −1) = 2x² −(8−15x). »
Exercice 4 (16 points)
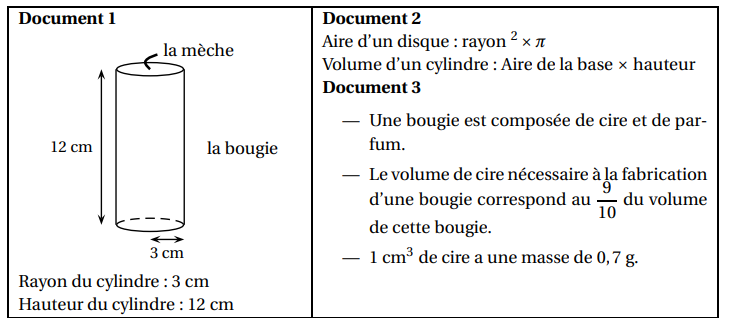
Une usine fabrique des bougies parfumées en cire de forme cylindrique.
Les questions 1, 2 et 3 sont indépendantes
1. a. Montrer que le volume d’une bougie est d’environ 339 .
b. Quelle est la masse de cire nécessaire pour une bougie ? On donnera une valeur
approchée au gramme près.
2. Au mois de novembre, l’usine a fabriqué des bougies de 4 parfums différents :
vanille, miel, lavande et jasmin.
Le diagramme circulaire codé ci-dessous donne la répartition, pour le mois de novembre, du nombre de
bougies fabriquées en fonction de leur parfum.
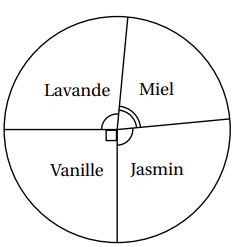
Les bougies au miel représentent 22 % de la production du mois de novembre.
Quel est le pourcentage de bougies à la lavande fabriquées au mois de novembre ?
3. Durant les trois premiers mois de l’année suivante, l’entreprise se donne pour objectif
de produire en moyenne 7 900 bougies par mois.
En janvier, elle fabrique 6 500 bougies et 8 000 en février.
Quel est le nombre de bougies à produire en mars pour atteindre l’objectif ?
Exercice 5 (23 points)
On dispose d’une roue dont les 4 secteurs ont tous la même aire et sont numérotés :
1; 2; 3; 4.
On dispose également d’une urne contenant 3 boules numérotées : 2; 3 et 4.
Les boules sont indiscernables au toucher.
On considère l’expérience aléatoire suivante :
« On fait tourner la roue puis on tire au hasard une boule dans l’urne.
On forme alors un nombre entier à deux chiffres tel que :
• Le chiffre des dizaines est le numéro indiqué par la flèche sur la roue.
• Le chiffre des unités est le numéro de la boule tirée dans l’urne. »
Exemple : Si la flèche indique le numéro 1 sur la roue et que la boule tirée dans l’urne porte
le numéro 3, on forme le nombre 13.
1. Écrire la liste des 12 issues possibles.
2. Déterminer la probabilité de l’évènement : « Obtenir un nombre impair ».
3. On considère l’évènement A : « Le nombre formé est un nombre premier et inférieur à
30 ».
a. Quelle est la probabilité de l’évènement A?
b. Quelle est la probabilité de son évènement contraire ?
À l’aide de cette expérience aléatoire, on crée un jeu de hasard.
Le joueur gagne s’il obtient un multiple de 11.
4. Montrer que la probabilité d’obtenir un multiple de 11 est égale à 0,25.
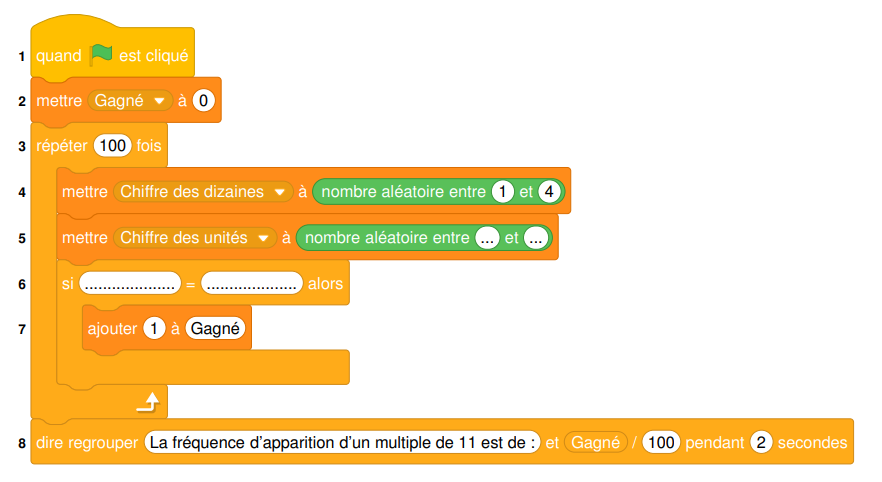
5. On souhaite simuler ce jeu à l’aide d’un logiciel de programmation.
On a rédigé le script ci-dessous :
Information :
a. Écrire sur la copie comment compléter les deux cases vides de la ligne 5.
Ne pas justifier.
b. Écrire sur la copie comment compléter les deux cases vides de la ligne 6.
Ne pas justifier.
c. On a cliqué sur le drapeau et voici le résultat du programme :
« La fréquence d’apparition d’un multiple de 11 est 0,23. »
Pourquoi le résultat est-il différent de celui obtenu dans la question 4 ?
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2024 : réviser avec le sujet et son corrigé» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
