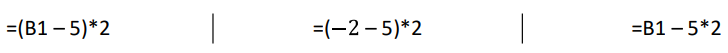Cette épreuve porte sur les notions suivantes :
- Un QCM sur scratch, les fractions, les puissances et le calcul de masses;
- L’étude d’une cabane avec le théorème de Thalès, la trigonométrie dans le triangle rectangle;
- L’étude d’un bac à sable avec des calculs de volumes et de la proportionnalité;
- Deux programmes de calcul et du calcul littéral avec une équation-produit;
- L’étude d’une urne avec les probabilités;
- Arithmétique avec la décomposition en facteurs premiers;
- L’étude de tarifs de location de bateaux électrique avec une fonction linéaire et une fonction affine.
Ce sujet du brevet de maths 2023 est à télécharger en PDF ainsi que, son corrigé afin de réviser le brevet du collège.
DIPLÔME NATIONAL DU BREVET SESSION 2023
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 100 points
Exercice 1 (18 points)
Cet exercice, en deux parties, est un questionnaire à choix multiples (QCM). Pour chaque question,
parmi les réponses proposées, une seule est exacte.
Recopier le numéro de la question et indiquer la réponse choisie. Aucune justification n’est attendue ici.
Partie A
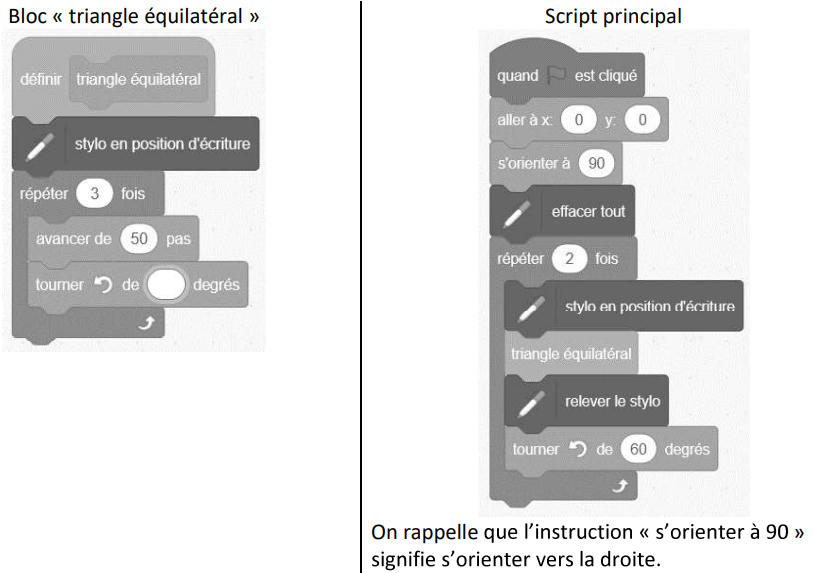
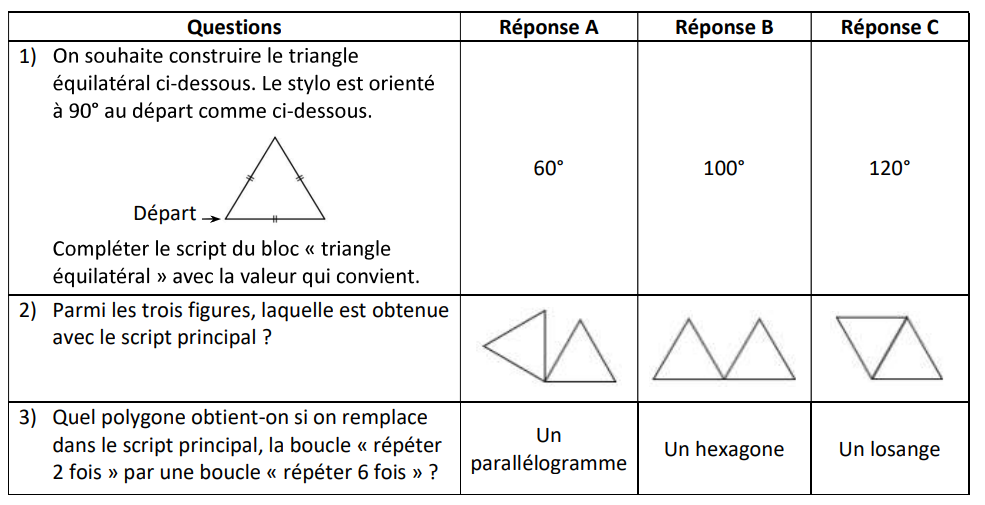
Dans cette partie, on s’intéresse au programme ci-dessous, composé d’un bloc « triangle équilatéaral » et d’un script principal :
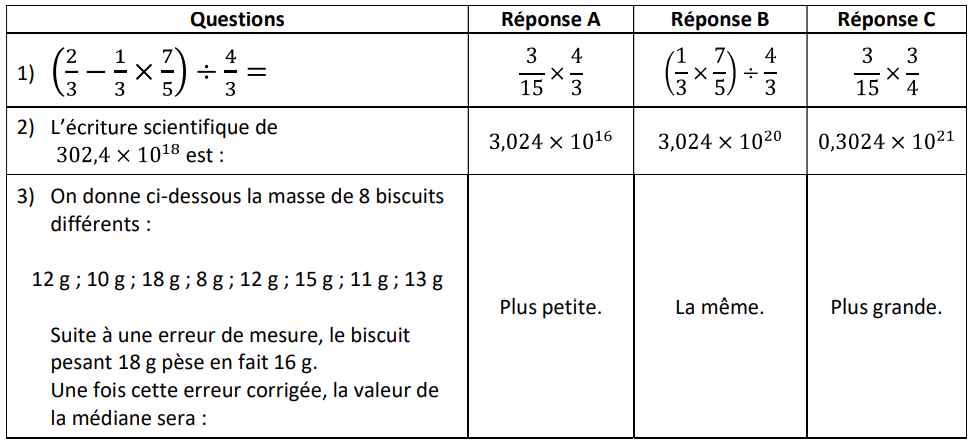
Partie B
Exercice 2 (24 points)
Les 3 parties de cet exercice sont indépendantes et peuvent être traitées séparément.
Une famille souhaite installer dans son jardin la cabane ci-dessous. La partie inférieure de cette cabane, encadrée par des pointillés sur la photo, est modélisée par le schéma à droite :
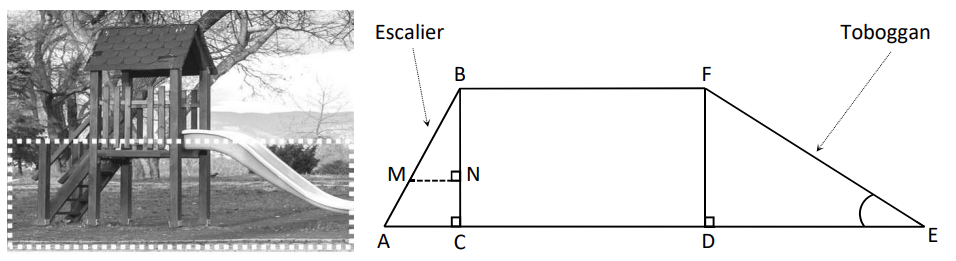
On précise que :
AB = 1,3 m, AC = 0,5 m, BC=DF= 1,2 m, DE = 2,04 m.
Les triangles ABC, BMN et FDE sont rectangles.
Partie A : Étude du toboggan.
1) Pour que le toboggan soit sécurisé, il faut que 
mesure 30°, au degré près.
Le toboggan de cette cabane est-il sécurisé ?
2) Montrer que la rampe du toboggan, EF, mesure environ 2,37 m.
Partie B ; étude de l’échelle.
Pour consolide l’échelle, on souhaite ajouter une poutre supplémentaire [MN], comme indiqué sur le modèle.
1) Démontrer que les droites (AC) et (MN) sont parallèles.
2) On positionne cette poutre [MN] telle que BN = 0,84 m. Calculer sa longueur MN.
Partie C : Étude du bac à sable.
Un bac à sable est installé sous la cabane. Il s’agit d’un pavé droit dont les dimensions sont données ci-dessous :
1) Calculer le volume de ce bac à sable en .
2) On admet que le volume du bac à sable est de 0,72 .
On remplit entièrement ce bac avec un mélange de sable à maçonner et de sable fin dans le ratio 3 : 2.
Vérifier que le volume nécessaire de sable à maçonner est de 0,432 et que celui de sable fin est
de 0,288 .
3) Un magasin propose à l’achat le sable à maçonner et le sable fin, vendus en sac.
D’après les indications ci-dessous, quel est le coût total du sable nécessaire pour remplir entièrement ce bac à sable sachant qu’on ne peut acheter que des sacs entiers ?
Exercice 3 (15 points)
Amir et Sonia ont chacun inventé un programme de calcul.
1) Montrer que si le nombre choisi au départ est 6 alors on obtient et on obtient 38 avec celui de Sonia.
2) Amir et Sonia souhaitent savoir s’il existe des nombres choisis au départ pour lesquels les deux programmes renvoient le même résultat.
Pour cela, ils complètent la feuille de calcul ci-dessous :
Aucune justification n’est attendue pour les deux questions ci-dessous.
a) Parmi les trois propositions suivantes, recopier sur votre copie la formule qui a été saisie dans la cellule B2 avant d’être étirée vers la droite .
b) En vous aidant de la feuille de calcul, quel nombre doivent-ils choisir pour obtenir des résultats
égaux avec les deux programmes ?
3) Sonia et Amir souhaitent vérifier s’il existe d’autres nombres permettant d’obtenir des résultats égaux Pour cela, ils décident d’appeler le nombre choisi au départ de chacun des programmes.
a) Montrer que le résultat obtenu avec le programme de Sonia est donné par .
b) On admet que les programmes donnent le même résultat si on choisit comme nombre de départ les solutions de l’équation .
Résoudre cette équation et en déduire les valeurs pour lesquelles les deux programmes de calcul renvoient le même résultat.
Exercice 4 (22 points)
Des élèves organisent, pour leur classe, un jeu au cours duquel il est possible de gagner des lots.
Pour cela, ils placent dans une urne trois boules noires numérotées de 1 à 3, et quatre boules rouges
numérotées de 1 à 4, toutes indiscernables au toucher.
Partie A : étude du jeu.
1) On pioche au hasard une boule dans l’urne.
a) Quelle est la probabilité de tirer une boule rouge ?
b) Quelle est la probabilité de tirer une boule dont le numéro est un nombre pair ?
2) Le jeu consiste à piocher, dans l’urne, une première boule, la remettre dans l’urne puis en piocher une seconde.
Pour chacune des boules tirées, on note la couleur ainsi que le numéro.
Pour gagner un lot, il faut tirer la boule rouge numérotée 1 et une boule noire.
Quelle est la probabilité de gagner ?
Partie B : constitution des lots.
Pour constituer les lots, on dispose de 195 figurines et 234 autocollants.
Chaque lot sera composé de figurines ainsi que d’autocollants . Tous les lots sont identiques.
Toutes les figurines et tous les autocollants doivent être utilisés.
1) Peut-on faire 3 lots ?
2) Décomposer 195 en produit de facteurs premiers.
3) Sachant que la décomposition en produit de facteurs premiers de 234 est :
a) Combien de lots peut-on constituer au maximum ?
b) De combien de figurines et d sera alors composé chaque lot ?
Exercice 5 (21 points)
Pour se promener le long d’un canal, deux sociétés proposent une location de bateaux électriques.
Les bateaux se louent pour un nombre entier d’heure.
1) Étude du tarif proposé par la société A
Pour la société A, le prix à payer en fonction de la durée de location en heure est donné par le
graphique en ANNEXE.
Répondre aux questions ci-dessous à l’aide du graphique.
Aucune justification n’est attendue pour les questions a) et b).
a) Quel prix va-t-on payer en louant un bateau pour 2 heures ?
b) On dispose d’un budget de 100 €, combien d’heures entières peut-on louer un bateau ?
c) Expliquer pourquoi le prix est proportionnel à la durée de location.
d) En déduire à l’aide d’un calcul, le prix à payer pour une durée de location de 10 heures.
2) Étude du tarif proposé par la société B.
La société B propose le tarif suivant : 60 € de frais de dossier plus 15 € par heure de location.
a) Montrer qu’en louant un bateau pour une durée de deux heures, le prix à payer sera de 90 €.
b) On désigne par le nombre d’heures de location.
On appelle la fonction qui, au nombre d’heures de location, associe le prix, en euro, avec le tarif proposé par la société B.
On admet que est définie par : .
Sur le graphique donné en ANNEXE à rendre avec la copie, tracer la courbe représentative de la fonction .
c) Le prix payé est-il proportionnel à la durée de location ?
3) Comparaison des deux tarifs.
a) On souhaite louer un bateau pour une durée de 3 heures. Quelle société doit-on choisir pour
avoir le tarif le moins cher ? Quel prix va-t-on payer dans ce cas ?
b) Pour quelle durée de location le prix payé est-il identique pour les deux sociétés ?
ANNEXE
À compléter et à rendre avec la copie
Exercice 5 :
Prix payé pour la location d’un bateau en fonction de la durée de location.
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
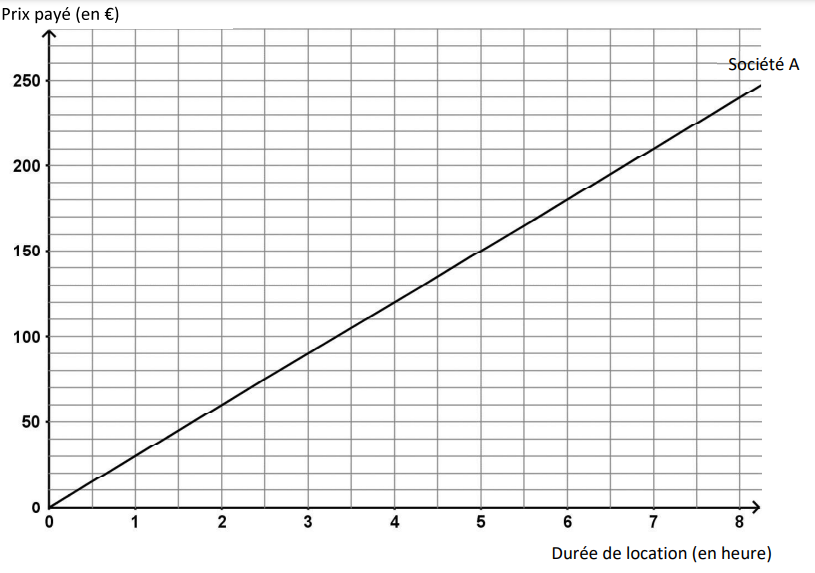
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «amérique du nord : brevet de maths 2023 avec sujet et corrigé en PDF.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
