Volumes et sections : exercices de maths en 3ème corrigés à télécharger en PDF

Exercice 1 – Volume et masse d’un lingot d’or (volumes et sections)

Un lingot d’or ayant la forme d’un parallélépipède rectangle et a les dimensions suivantes

– Longueur L = 7,5 cm ;
– largeur l = 3 cm ;
– hauteur h = 2,3 cm

On sait que la masse volumique de l’or est \(19{,}3\text{ g/cm}^3\).

1. Calculer le volume de ce lingot d’or.
2. Calculer la masse de ce lingot d’or.
3. On décide de reproduire ce lingot en l’agrandissant à l’échelle 3.

Quel sera alors le volume de la maquette obtenue ? Justifier la réponse.

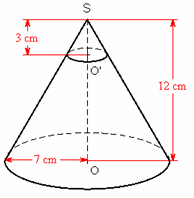
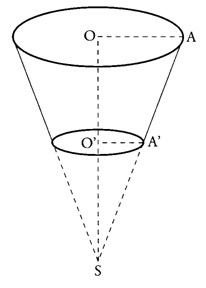
Exercice 2 – Réservoir d’eau

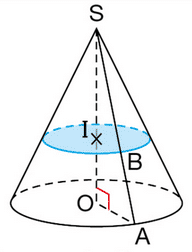
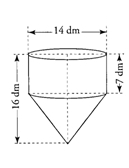
Un réservoir d’eau est formé d’une partie cylindrique et d’une partie conique.

1. Donner, en dm³, le volume exact de la partie cylindrique en utilisant le nombre\(\pi\).

2. Donner, en dm³, le volume exact de la partie conique en utilisant le nombre \(\pi\).

3. Donner le volume exact du réservoir, puis sa valeur arrondie à 1 dm³ près.

4. Ce réservoir peut-il contenir 1000 litres? Justifier la réponse.

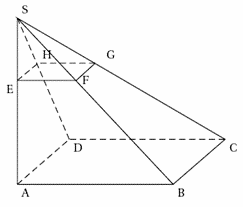
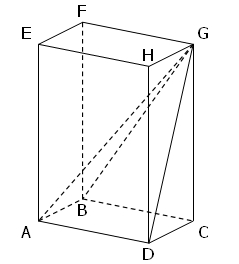
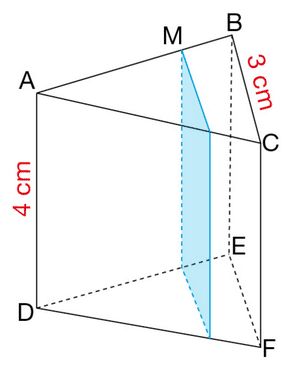
Exercice 3 – Bloc de pierre et prisme droit à base trapézoïdale (volumes et sections)

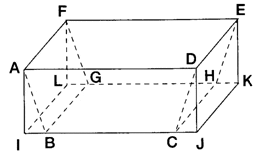
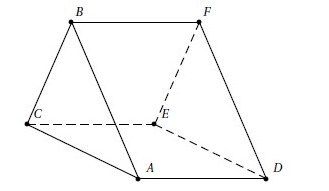
D’un bloc de pierre ayant la forme d’un pavé droit ADEFIJKL,

un sculpteur veut extraire le prisme droit ABCDFGHE ayant pour base le trapèze isocèle ABCD.

On donne : AD = 40 cm  ;  AI = 15 cm  ;  AF = 20 cm  ;  IB = 5 cm.

1) a) Calculer l’aire du trapèze ABCD.

b) Calculer le volume du prisme ABCDFGHE.

2) Calculer AB (donner la valeur exacte).

3) Calculer \(\tan(\widehat{BAI})\).

En déduire la valeur arrondie de \(\widehat{BAI}\)  à un degré près.

Exercice 4 – Volume d’un ballon de basket et d’une balle de tennis

1. On admet qu’un ballon de basket est assimilable à une sphère de rayon R₁ = 12,1 cm.

Calculer le volume V₁, en cm³, de ce ballon; donner le résultat arrondi au cm³.

2. On admet qu’une balle de tennis est assimilable à une sphère de rayon R₂, en cm.

La balle de tennis est ainsi une réduction du ballon de basket. Le coefficient de réduction est \(\frac{4}{15}\) .

a) Calculer R₂ ; donner le résultat arrondi au mm.

b) Sans utiliser cette valeur de R₂, calculer le volume V₂, en cm³, d’une balle de tennis ; donner le résultat arrondi à l’unité.
Rappel : Volume d’une sphère de rayon R : \(V=\frac{4}{3}\pi\times R^3\)

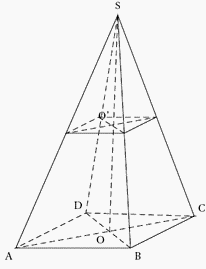
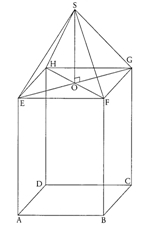
Exercice 5 – Problème du pigeonnier (volumes et sections)

Un pigeonnier est composé d’un parallélépipède rectangle ABCDEFGH et d’une pyramide SEFGH dont la hauteur [SO] mesure 3,1 m.

On sait que AB = 3 m, BC = 3,5 m et AE = 4 m.

1.Calculer la longueur BD et en déduire celle de BH.

On donnera des valeurs approchées de ces résultats à \(10^{-1}\) près.

2. Calculer en \(m^3\) le volume \(V_1\)  de ce pigeonnier.

3. Un modéliste désire construire une maquette de ce pigeonnier à l’échelle \(\frac{1}{24}\).

Calculer en \(dm^3\) le volume \(V_2\) de la maquette.

On donnera une valeur approchée de ce résultat à \(10^{-3}\) près.

Exercice 6 – La pyramide du Louvre

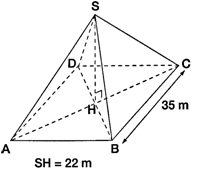
La pyramide du Louvre est une pyramide régulière à base carrée de 35 m de côté, sa hauteur est 22 m.

1) Calculer l’aire de sa base.

2) Calculer la valeur exacte du volume V de cette pyramide.

Donner la valeur arrondie de V au mètre cube.

3) Dans un parc de loisirs, on construit une réduction de cette pyramide ; le côté de la base carrée mesure 7 m.

a) Calculer l’échelle de cette réduction.

b) Calculer la hauteur de la pyramide réduite.

c) Par quel nombre faut-il multiplier le volume V de la pyramide du Louvre pour obtenir le volume V’ de la pyramide réduite ?

Exercice 7 – Cornet de glace et quantité de glace (volumes et sections)

Un cornet de glace est formé par un cône de révolution de hauteur 10 cm et une demi-boule de rayon 3 cm.

le cône est rempli complétement de glace.

Calculer la quantité nécessaire de glace, en cL, nécessaire pour confectionner ce cornet.

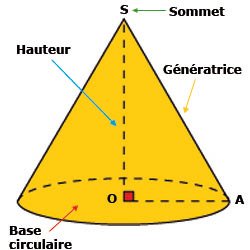
Exercice 8 – Volume d’un cône de révolution et sections de solides

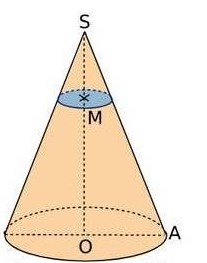
Le cône de révolution ci-dessous de sommet S a une hauteur [SO] de 9 cm et un rayon de base [OA] de 5 cm.

a. Calculer le volume \(V_1\) de ce cône au  \(cm^3\) près.

b. Soit M le point du segment [SO] tel que SM = 3 cm.

On coupe le cône par un plan parallèle à la base passant par M.

Calculer le rayon de cette section.

c. Calculer le volume \(V_2\)  du petit cône de sommet S ainsi obtenu au \(cm^3\) près.

Exercice 9 – Tajine et calcul du volume d’un cône (volumes et sections)

Une Tajine est un plat composé d’une assiette circulaire

et d’un couvercle en forme de cône qui s’emboîte parfaitement sur l’assiette .

L’assiete de ce tajine a un rayon [OA] qui mesure 15 cm et la géneratrice du cône [SA] mesure 25 cm .

1) Calculer la hauteur OS du cône .

2) Montrer que la valeur exacte du volume du cône est égale à \(1500\pi\,cm^3\) .

Exercice 10 – Volume d’un prisme droit

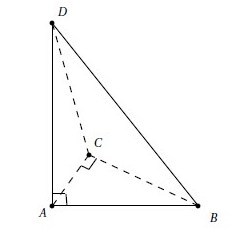
Calculer le volume de ce prisme droit sachant que :

ABC est rectangle et isocèle en B

et BA = BC = BF = 5 cm .

Exercice 11 – Calcul du volume d’un prisme droit (volumes et sections)

Calculer le volume de la pyramide ABCD (un tétraèdre) sachant que :

ABC est rectangle en C et CB = 5 cm , CA = 4 cm et AD = 7 cm .

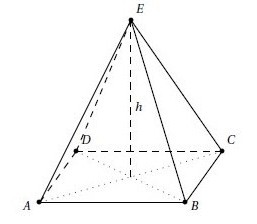
Exercice 12 – Calculer le volume d’une pyramide

Calculer le volume de cette pyramide sachant que :

ABCD est un carré de 8 cm et h = 11 cm .

Arrondir le résultat au centième de cm³ près.

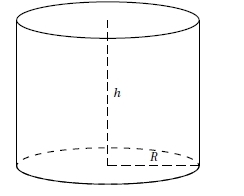
Exercice 13 – Calcul du volume d’un cylindre (volumes et sections)

Calculer le volume du cylindre ci-dessous, sachant que  :

R= 3 cm et h = 5 cm (donner le résultat au centième de cm³ près).

Exercice 14 – Calculer le volume de ce cône de révolution

sachant que SO = 8 cm et OA = 6 cm (arrondir le résultat au centième de cm³ près).

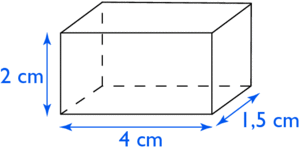
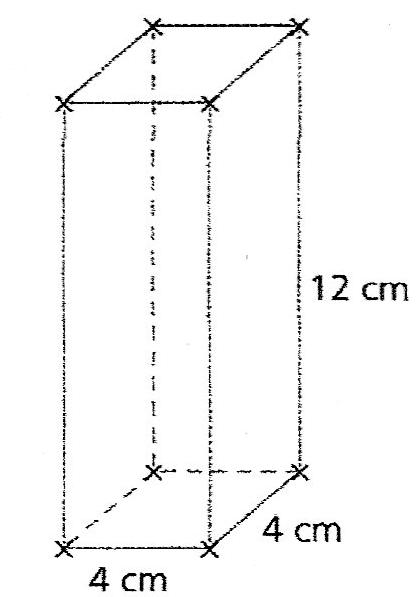
Exercice 15 – Volume d’un parallélépipède rectangle ou pavé droit (volumes et sections)

Calculer le volume du pavé droit (parallélépipède rectangle ) suivant :

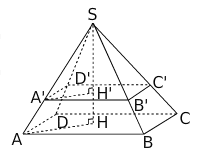
Exercice 16 – Volume du tronc d’une pyramide

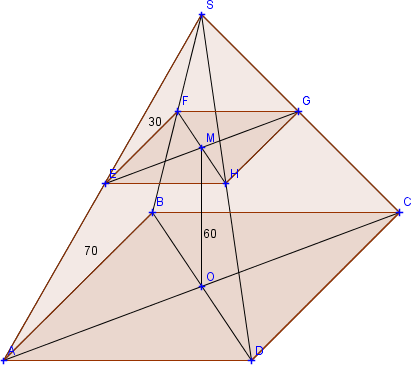
1/Le bac à fleurs ABCDEFGH est un tronc de pyramide qui a été formé en coupant la pyramide régulière SABCD par un plans parallèle a sa base.

ABCD et EFGH sont deux carrés de centres respectif O et M .

On donne:AB=70cm;EF=30cm et OM=60cm .

On note h la hauteur SO en cm .

a.Exprimer de deux facons différentes,SM en fonction de h.

b.En déduire une equation dont h est solution.

c.Résoudre cette équation afin de trouver la valeur de h.

d.Calculer le volume de ce bac a fleurs.

2/Voici comment le mathématicien hindou Bhaskara calculait le volume d’un tronc de pyramide au XII eme siecle:

La somme des aire des base et de l’aire d’un rectangle de largueur la somme des largueur des base et de longueurla somme des longueur des base,étant diviser par six puis multiplier par la profondeur donne le volume.

Appliquer cette methode pour calculer le volume du bac a fleur ci-dessus :

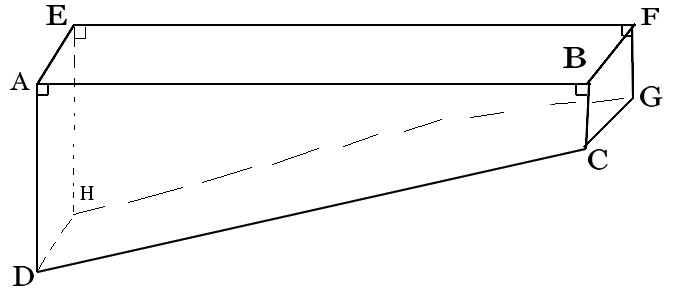
Exercice 17 – Volume d’un prisme (volumes et sections)

On donne: AB =6 m, AE = 5m, AD = 1.80m, BC = 0.80m .

Sur le schéma ci dessus, les dimensions ne sont pas respectées.

1. Montrer que le volume ce cette piscine est 39 m^{3 .}

2. A la fin de l’été, M.Dujardin vide sa piscine à l’aide d’une pompe dont le débit est 5m³ par heure. Calculer le nombre de m³ restant dans la piscine au bout de 5 heures.

Exercice 18 – Géométrie dans l’espace

On a représenter ci-contre un réservoir parallélépipédique permettant de mesurer la hauteur d’eau tombée dans un jardin pendant une averse (voir ci-dessous)

1. On assimile les gouttes d’eau à des boules de diamètre 4mm.

Calculer le volume d’une goutte d’eau. Donner leur valeur exacte.

2. La hauteur d’eau tombée pendant cette averse est égale à 8cm.

Calculer le nombre de gouttes d’eau contenues dans le réservoir. On donnera la valeur approché par défaut.

Exercice 19 – Coefficient de réduction et pyramide (volumes et sections)

Une pyramide SABCD à base rectangulaire par un plan parallèle à base à 5 cm du sommet . AB=4,8cm ; BC=4,2cm et SH=8cm.

a. Calculer le coefficient de K de réduction entre les pyramides SABCD et SA’B’C’D’ .

b. Calculer le volume de la pyramide SABCD .

c. En déduire le volume de la pyramide SA’B’C’D’ .

Exercice 20 – Volume et aire d’une boule

une boule de laiton mesure 10cm de diamètre.

Le laiton est un alliage constitué de 40% de zinc est de 60% de cuivre.

1)Calculer le volume de cette boule.(arrondir a 1/10cm3 près)

2)On veut recouvrir cette boule de peinture dorée.

a)Calculer l’aire de la surface de la boule.

Donner la valeur exacte.

b)De quelle quantité de peinture est nécessaire si 1dl recouvre 0.1m²?

3) la boule est sciée selon un plan situé à 3cm de son centre.

a)calculer le rayon du cercle de section, la longueur de ce cercle et l’aire du disque de section.

Donner les valeurs exactes puis les valeurs arrondies au cm près et cm² près.

Exercice 21 – Coefficient de réduction (volumes et sections)

Sur la figure ci-dessous, on a un cône de révolution tel que SO = 12 cm.

Un plan parallèle à la base coupe ce cône tel que SO’ = 3 cm.

1. Le rayon du disque de base du grand cône est de 7 cm.

Calculer la valeur exacte du volume du grand cône.

2. Quel est le coefficient de réduction qui permet de passer du grand cône au petit cône ?

3. Calculer la valeur exacte du volume de ce petit cône, puis en donner la valeur arrondie au \(cm^3\) .

Exercice 22 – Volume d’une pyramide à base carrée

Sur la figure ci-dessous, SABCD est une pyramide à base carrée de hauteur [SA] telle que AB = 9 cm et SA = 12 cm.

Le triangle SAB est rectangle en A.

EFGH est la section de la pyramide SABCD par le plan parallèle à la base et telle que SE = 3 cm.

1.a. Calculer EF.

b. Calculer SB.

2.a. Calculer le volume de la pyramide SABCD.

b. Donner le coefficient de réduction permettant de passer de la pyramide SABCD à la pyramide SEFGH.

c. En déduire le volume de SEFGH.On donnera une valeur arrondie à l’unité.

Exercice 23 – Volume d’une pyramide (volumes et sections)

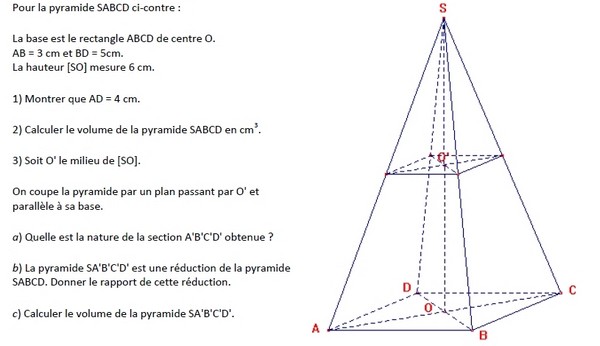
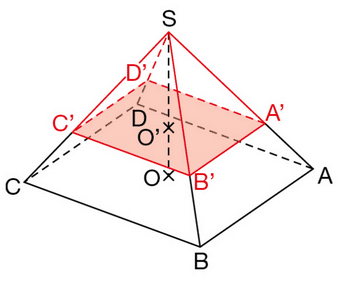
Pour la pyramide SABCD ci-dessous, la base est le rectangle ABCD de centre O.

AB = 3 cm et BD = 5 cm.La hauteur [SO] mesure 6 cm.

1. Montrer que AD = 4 cm.

2. Calculer le volume de la pyramide SABCD en \(cm^3\).

3. Soir O ‘ le milieu de [SO].On coupe la pyramide par un plan passant par O ‘ et parallèle à sa base.

a. Quelle est la nature de la section A’B’C’D’ obtenue ?

b. La pyramide SA’B’C’D’ est une réduction de la pyramide SABCD.

Donner le rapport de cette réduction.

c. Calculer le volume de la pyramide SA’B’C’D’.

Exercice 24 – Volume d’un cône de révolution

Exercice 25 – Boîte de balles de tennis (volumes et sections)

Une boîte cylindrique contient 3 balles de tennis de rayon 3,4 cm.

a) Fais une figure,dans le cas où la boite a des dimensions minimales.
b) Quelles sont les dimensions minimales de cette boîtes(hauteur et rayon) ?
c) Calcule le volume de la boîte et le volume des trois balles.
d) Calcule le pourcentage de « vide » dans cette boîte contenant les 3 balles .

Exercice 26 – Volume d’un verre conique

Dans un verre conique de hauteur 8 cm et de rayon 6 cm,

je mets 3 boules de glace de rayon 3 cm chacune.

Je n’ai pas le temps de les manger!! trop de copies à corriger.

Les 3 boules fondent!!

La glace va t-elle déborder ?? si oui, combien de cL de glace ai-je perdu?

Exercice 27 – Spectacle de magie : le souci du magicien (volumes et sections)

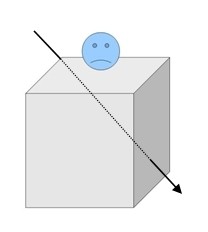
Pour son spectacle, un magicien veut enfoncer des épées dans une boîte dans laquelle serait enfermé un spectateur.

La boîte est un cube de 1 m de côté.

Pour son projet, le magicien doit faire fabriquer des épées.

Il lui faut des épées toutes de même taille telles que, quel que soit l’endroit où il  enfonce l’épée, elle puisse dépasser d’au moins 10 cm.

Quelle longueur minimum de lame d’épée doit-il commander au forgeron ?

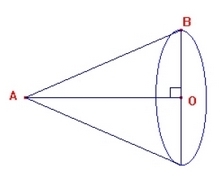
Exercice 28 – Cône de révolution et extrait du brevet

On considère un cône de révolution semblable à celui qui est représenté ci-dessous avec AO = 2 cm et BO = 3 cm.

1. Calculer la longueur de la génératrice [AB] et donner la valeur exacte en cm puis la valeur arrondie à l’unité.

2. Calculer le volume du cône et donner, en  \(cm^3\) , la valeur exacte puis la valeur arrondie à l’unité.

Exercice 29 – Pavé droit et extrait du brevet (volumes et sections)

ABCDEFGH est un parallélépipède rectangle. On donne AE = 3 m ; AD = 4 m ; AB = 6 m.

1) a) Que peut-on dire des droites (AE) et (AB) ? Le justifier.

b) Les droites (EH) et (AB) sont-elles sécantes ?

2) a) Calculer EG. On donnera la valeur exacte.

b) En considérant le triangle EGC rectangle en G, calculer la valeur exacte de la longueur de la diagonale [EC] de ce parallélépipède rectangle.

3) Montrer que le volume de ABCDEFGH est égal à 72 m³.

4) Montrer que l’aire totale de ABCDEFGH est égale à 108 m².

Exercice 30 – Pyramides au brevet de maths

Pour la pyramide SABCD ci-dessous :

La base est le rectangle ABCD de centre O. AB = 3 cm et BD = 5 cm. La hauteur [SO] mesure 6 cm.

1) Montrer que AD = 4 cm.

2) Calculer le volume de la pyramide SABCD en cm³.

3) Soit O’ le milieu de [SO]. On coupe la pyramide par un plan passant par O’ et parallèle à sa base.

a) Quelle est la nature de la section A’B’C’D’ obtenue ?

b) La pyramide SA’B’C’D’ est une réduction de la pyramide SABCD. Donner le rapport de cette réduction.

c) Calculer le volume de la pyramide SA’B’C’D’.

Exercice 31 – Volume d’un pot de fleur (volumes et sections)

Un pot à fleurs a la forme d’un tronc de cône.

Ses deux disques de base ont 10 cm et 20 cm de rayon.

La distance entre leurs centres O et O’ est 30 cm.

Sur la figure (OA) et (O’A’) sont parallèles.

1.  Montrer que \(\dfrac{SO^{\prime}}{SO}=\dfrac{1}{2}\).

Montrer que SO = 60 cm.

2.  Calculer le volume du cône de sommet S et de base le disque de

centre O.

3. Calculer le volume du pot.

On ne demande pas de refaire une figure.

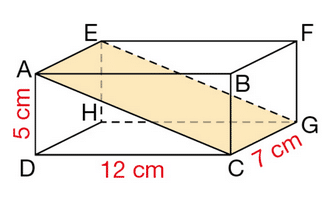
Exercice 32 – Volume et espace

ABCDEFGH est un pavé droit à base carrée. On donne AD = 3 cm et DC =2cm et CG = 4 cm.

1.Calculer le volume en cm³ de la pyramide de sommet G et de base ABCD.

2.Calculer DG.

3. On admet que le triangle ADG est rectangle en D.

Calculer la mesure, arrondie au degré, de l’angle AGD.

Calculer la valeur exacte de la longueur AG, puis en donner la valeur arrondie au millimètre.

Exercice 33 – Calculs de volumes (volumes et sections)

Un pigeonnier est composé d’un parallélépipède rectangle ABCDEFGH et d’une pyramide SEFGH dont la hauteur [SO] mesure 3,1 m.

On sait que AB = 3 m, BC = 3,5 m et AE = 4 m.

1.Calculer la longueur BD et en déduire celle de BH. On donnera des valeurs approchées de ces résultats à 10^-1 près.

2. Calculer en m³ le volume V₁  de ce pigeonnier.

3. Un modéliste désire construire une maquette de ce pigeonnier à l’échelle \(\frac{1}{24}\).

Calculer en dm³ le volume V₂ de la maquette.

On donnera une valeur approchée de ce résultat à 10^-3 près.

Exercice 34 :

On réalise la section d’une pyramide SABCD à base rectangulaire par un plan parallèle

à sa base à 5 cm du sommet.

Nous avons AB=4,8 cm; BC = 4,2 cm et SH = 8 cm.

1. Calculer le volume de la pyramide SABCD.
2. La pyramide SA’B’C’D’ est une réduction de la pyramide SABCD.
3. Donner le rapport de cette réduction.
4. En déduire le volume de la pyramide SA’B’C’D’.

Exercice 35 (volumes et sections)

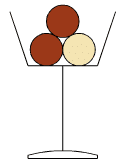
Un restaurant propose en dessert des coupes de glace composées de trois boules

supposées parfaitement sphériques, de diamètre 4,2 cm.

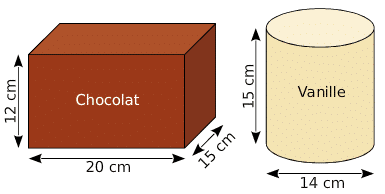
Le pot de glace au chocolat ayant la forme d’un parallélépipède rectangle est plein,

ainsi que le pot de glace cylindrique à la vanille.

Le restaurateur veut constituer des coupes avec deux boules au chocolat et une boule à la vanille.

1. Montrer que le volume d’un pot de glace au chocolat est de 3 600 \(cm^3\).

2.Calculer la valeur arrondie au \(cm^3\) du volume d’un pot de glace à la vanille.

3.Calculer la valeur arrondie au \(cm^3\) du volume d’une boule contenue dans la coupe.

4.Sachant que le restaurateur doit faire 100 coupes de glace, combien doit-il acheter

de pots au chocolat et de pots à la vanille ?

Exercice 36 :

Une pyramide régulière de sommet S et de hauteur SO = 9 cm a pour
base un carré ABCD de côté 4,5 cm.

Elle est coupée par un plan parallèle à sa base qui coupe sa hauteur en O’, tel que SO’ = 6 cm.

a. Quelle est la nature de la section A’B’C’D’?

b. Calculer le volume de la pyramide réduite SA’B’C’D’.

Exercice 37 (volumes et sections)

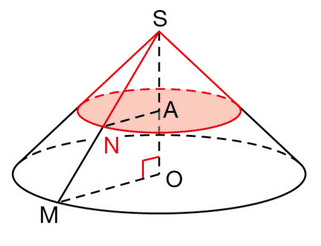
Un cône de hauteur SO = 18 cm a pour base un disque de rayon 15 cm.
A est le point de la hauteur [SO] tel que SA=10 cm.

Le plan passant par A et parallèle à la base coupe le segment [SM] en N.
Calculer le volume, en \(cm^3\), du cône réduit de sommet S et de base le disque de centre A et de rayon AN.
Donner une valeur approchée à l’unité près.

Exercice 38 :

Le rectangle bleu est la section du prisme droit ABCDEF par un plan parallèle à la face BCFE et
passant par un point M de l’arête [AB].

Donner la nature et la (ou les) dimension(s) de cette section :

a. lorsque M est en A,

b. lorsque M est en B,

c. lorsque M est le milieu de [AB].

Exercice 39 (volumes et sections)

En coupant ce parallélépipède rectangle par le plan passant par A et C et parallèle à l’arête [DH],
on obtient la section AEGC.

a. Quelle est sa nature ?
b. Dessiner cette section en vraie grandeur.
c. Calculer la longueur AC, en cm.

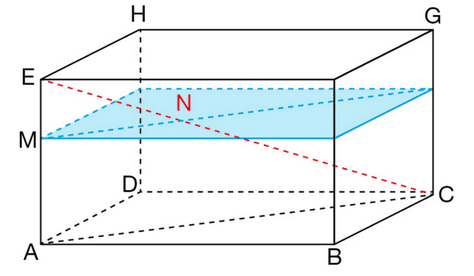
Exercice 40 :

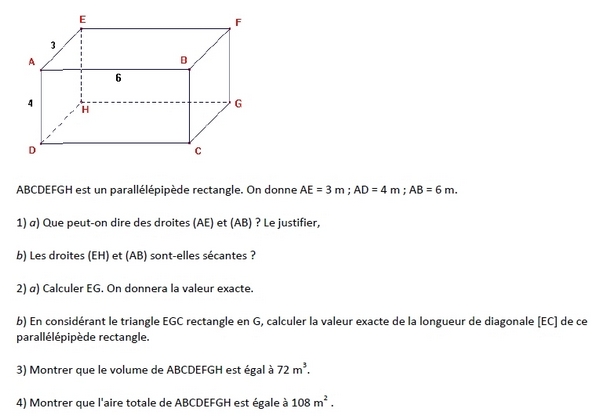
ABCDEFGH est un parallélépipède rectangle tel que AB = 12 cm, AD=5 cm, AE=8 cm.
Le point M de [AE] est tel que AM =6 cm.
La section de ce solide par un plan parallèle à la face ABCD et passant par M est représentée en bleu.

a. Utiliser le théorème de Pythagore pour calculer AC.
b. Utiliser le théorème de Thalès pour calculer MN.

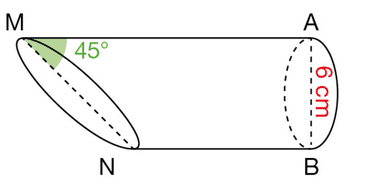
Exercice 41 (volumes et sections)

Pour créer une lampe de décoration, une machine tranche un cylindre métallique selon les
données indiquées.

Calculer la valeur exacte de MN.

Exercice 42 :

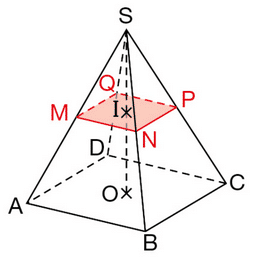
SABCD est une pyramide régulière à base carrée de côté 6 cm et de hauteur
[SO] avec SO = 7,5 cm.
Un plan parallèle à la base coupe [SO] en I de sorte que SI=2,5 cm.

La section est le quadrilatère MNPQ.

a. Calculer le volume \(V\), en \(cm^3\), de SABCD.

b. \(V^{\prime}\)  est le volume, en \(cm^3\), de SMNPQ.

Exprimer \(V^{\prime}\) en fonction de \(V\).

Donner une valeur approchée de \(V^{\prime}\) au centième près.

Exercice 43 :

Un cône de révolution \(\varphi\) de sommet S et de base un disque de centre O est coupé par un plan
parallèle à sa base.

La section est le cercle de centre I qui passe par B, point d’intersection du segment [SA] avec le plan.
a. Le cône \(\varphi^{\prime}\) de sommet S et dont la base est le disque de centre I passant par B est une réduction du cône \(\varphi\).
Écrire le rapport de réduction de trois façons différentes.

b. On donne SO =10 cm, OA=7,5 cm et SI=6 cm.
Dessiner la section en vraie grandeur.

Exercice 44 :

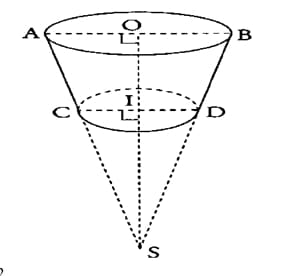
Un panier a la forme d’un tronc de cône dont les bases ont pour diamètres les segments [AB] et [CD], situés dans un même plan.

Le petit cône de sommet S et de disque de base de rayon [IC] est une réduction du grand cône de sommet S et de disque de base de rayon [OA].

Il est inutile de reproduire la figure ci-dessus, représentant un tronc de cône.

On donne : AB=30cm    CD = 20 cm

1. a) Démontrer, à partir des indications portées sur la figure, que les droites (AO) et (CI) sont parallèles.

b) Démontrer que \(\frac{SI}{SO}=\frac{2}{3}\).

2.a) Calculer le volume V₂ du petit cône en fonction du volume V₁ du grand cône.

b) Montrer que le volume V du tronc de cône est :

\(V=\frac{19}{27}V_1\).

Exercice 45 :

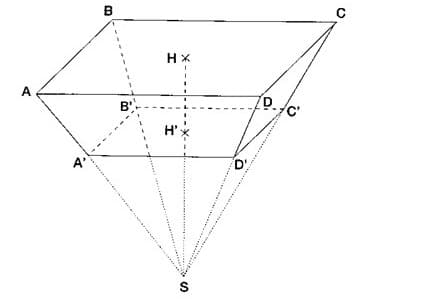
Une boîte de chocolats a la forme d’une pyramide tronquée (figure ci-dessous).

Le rectangle ABCD de centre H et le rectangle A’B’C’D’ de centre H’ sont dans des plans parallèles.

On donne :

AB = 6 cm

BC = 18 cm

HH’ = 8 cm

SH = 24 cm

1) Calculer le volume V₁ de la pyramide SABCD de hauteur SH.

2) Quel est le coefficient k de la réduction qui permet de passer de la pyramide SABCD à la pyramide SA’B’C’D’ de hauteur SH’ ?

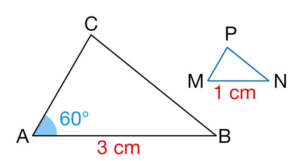
3) En déduire le volume V₂ de la pyramide SA’B’C’D’ puis le volume V₃ de la boîte de chocolats ?

Exercice 46 :

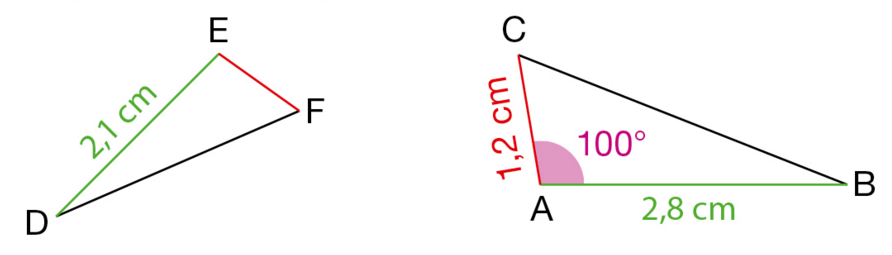
Le triangle MNP est une réduction du triangle ABC.
Dans quel rapport ?
En déduire la mesure de l’angle \(\widehat{NMP}\) .

Exercice 47 :

On veut remplir un récipient en forme de cylindre à l’aide d’un récipient de même
forme dont les dimensions sont 5 fois plus petites.
Combien de fois devra-t-on verser tout le contenu du petit dans le grand ?

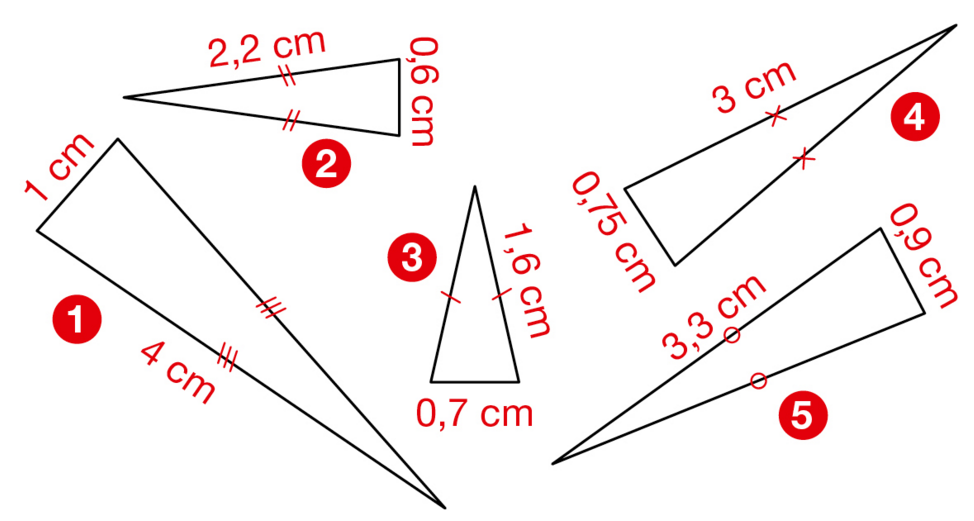
Exercice 48 :

Associer les triangles qui sont un agrandissement ou une réduction l’un de l’autre.

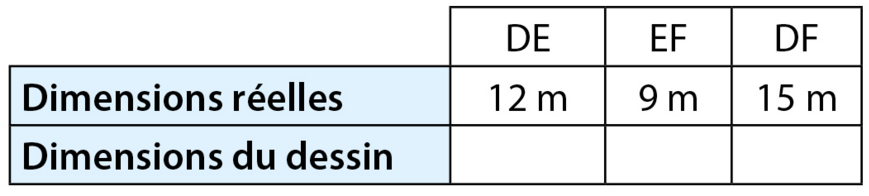
Exercice 49  :

On veut représenter à l’échelle \(\frac{1}{200}\) ce parc de jeux  triangulaire dont les dimensions
sont indiquées sur cette figure à main levée.

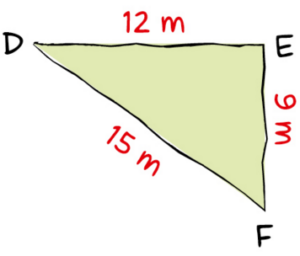
Donner les longueurs DE, EF et DF ci-dessous :

	DE	EF	DF
Dimensions réelles	12 m	9 m	15 m
Dimensions du dessin

Exercice 50  :

Le triangle DEF est une réduction dans le rapport k du triangle ABC.

a. Calculer le rapport k de réduction.
b. Calculer la longueur du segment [EF].
c. Donner la mesure de l’angle \(\widehat{DEF}\) .
2. Le triangle ABC est un agrandissement de rapport k’ du triangle DEF.

Donner la valeur exacte de k’.

Exercice 51  :

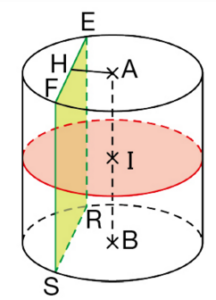
On a coupé par deux plans ce cylindre dont les bases sont deux disques de centres A et B ; les
sections sont représentées l’une en rose, l’autre en vert.
H est le milieu de [EF] et :
AH = 3 cm, AB = 8 cm, AE = 5 cm.
1. Donner la description de chacun des deux plans.
2. Construire en vraie grandeur :
a. la section rose ;
b. le triangle AEF puis la section verte.
3. a. Calculer EF.
b. Vérifier cette longueur sur le dessin en vraie grandeur.

Exercice 52  :

Pour chaque question, une seule réponse est exacte.

1. AMNE est la section de ce parallélépipède rectangle par un plan parallèle à l’arête [CG] (AD = 5 cm, DM = 5 cm et AE = 6 cm). La section AMNE est un…

• a. parallélogramme non rectangle
• b. rectangle de dimensions \(\sqrt{50}\) cm et 6 cm
• c. rectangle de dimensions 5 cm et 6 cm

2. Le cercle bleu de diamètre [A’B’] est la section de ce cône par un plan parallèle à sa base. AB = 5 cm et A’B’ = 3 cm. Le cône bleu est une réduction du grand cône dans le rapport…

• a. \(\dfrac{3}{5}\)
• b. \(\dfrac{5}{3}\)
• c. \(\dfrac{1}{2}\)

3. Le grand cône ci-dessus a pour volume \(12{,}5\pi\) cm³. Le cône bleu a pour volume environ…

• a. 8,48 cm³
• b. 23,56 cm³
• c. 82,46 cm³

Bien travailler avec volumes et sections

D’abord, cherche chaque exercice seul, sur une feuille de brouillon. Ensuite, vérifie chaque résultat avec soin. Ainsi, chaque erreur devient une occasion de progresser. Par ailleurs, volumes et sections en troisième demande surtout de la régularité.

Par exemple, explique la méthode à voix haute, comme à un camarade. Enfin, si tu veux approfondir, consulte la page Géométrie dans l’espace sur Wikipédia. Également, tu peux continuer avec statistiques : exercices de maths en 3ème corrigés en PDF.